Формы отчетности по практике

ЗАДАНИЕ НА УЧЕБНУЮ ПРАКТИКУ

Результаты наблюдений за торможением отцепа представлены выборкой отсчётов скорости его движения по парковой тормозной позиции сортировочной горки. Для микропроцессорной системы управления движением отцепов методом рекуррентной идентификации оценить параметры линейной модели динамики процесса , по полученным результатам построить прогноз момента окончания торможения. Для этого:

- вычислить последовательность коэффициентов 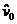, линейной модели динамики процесса;

- построить последовательность прогнозируемых значений момента окончания торможения отцепа;

- разработать структурную схему алгоритма вычислений и составить программу.

Расчётная скорость на выходе из замедлителей определяется длиной свободного участка паркового пути, удельным сопротивлением движению отцепа. При выполнении контрольной работы принять эту величину равной м/с, где 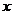- последняя цифра шифра. Значения скорости движения отцепа приведены в таблице 1, вариант выбирается по последней цифре учебного шифра. Дополнительная информация присутствует в приложении.

Таблица 1. Скорость движения отцепа

Время T, c	Скорость отцепа, м/с (номер варианта)
Время T, c	1	2	3	4	5	6	7	8	9	0
5,5	2,73	2, 8 7	2,95	3,06	3,15	3,26	3,35	3,46	3,55	2,69
5,6	2,7 2	2,8 6	2,9 4	3,0 5	3,1 4	2,2 5	3,3 4	3,4 5	3,5 4	2,6 8
5,7	2,7 1	2,8 5	2,9 3	3,0 4	3,1 3	3,2 4	3,3 3	3,4 4	3,5 3	2,6 7
5,8	2,66	2,78	2,88	3,0 3	3,1 2	3,2 3	3,27	3,35	3,47	2,6 6
5,9	2,6 5	2,7 7	2,8 7	3,02	3,09	3,17	3,2 6	3,3 4	3,4 6	2, 6 5
6,0	2,6 4	2,7 6	2,8 6	3,0 1	3,0 8	3,1 6	3,2 5	3,3 3	3,4 5	2,6 4
6,1	2,6 3	2,7 5	2,8 5	2, 98	3,0 7	3,1 5	3,2 4	3,3 2	3,4 4	2,6 3
6,2	2,6 2	2,7 4	2,8 4	2, 97	3,0 6	3,1 4	3,2 3	3,3 1	3,4 3	2,62
6,3	2,6 1	2,7 3	2,8 3	2,94	3,0 5	3,1 3	3,2 2	3,3 0	3,42	2,54
6,4	2,60	2,7 2	2,8 2	2,9 3	3,0 4	3,1 2	3,21	3, 29	3,4 1	2,5 3
6,5	2, 59	2,7 1	2,8 1	2, 92	3,0 2	3,11	3,2 0	3, 28	3,4 0	2,5 2
6,6	2, 58	2,7 0	2,8 0	2,91	3,0 1	3,1 0	3,15	3, 27	3, 39	2,5 1
6,7	2, 57	2, 69	2, 79	2,9 0	3,0 0	3,09	3,1 4	3,2 6	3,3 5	2,5 0
6,8	2,53	2,67	2,7 8	2, 89	2,9 6	3,05	3,1 3	3,2 5	3,34	2,49
6,9	2,5 2	2,6 6	2,7 7	2, 88	2,95	3,0 4	3,1 2	3,2 4	3,3 3	2,4 8
7,0	2,5 1	2,6 5	2,7 6	2,86	2,9 4	3,0 3	3,1 1	3,2 3	3,3 2	2,4 7
7,1	2,5 0	2,6 4	2,7 5	2,8 5	2,9 3	3,0 2	3,1 0	3,2 2	3,3 1	2,4 6
7,2	2, 49	2,6 3	2,7 4	2,8 4	2,9 2	3,0 1	3, 09	3,18	3,26	2,4 5
7,3	2,4 8	2,60	2,70	2,78	2,90	2,97	3, 08	3,1 7	3,2 5	2,4 4
7,4	2,4 7	2, 59	2, 69	2,7 7	2,85	2,9 6	3,06	3,1 6	3,2 4	2,4 3
7,5	2,35	2,48	2,58	2,67	2,75	2,87	2,95	3,06	3,17	2,3 2
7,6	2, 33	2,42	2,50	2,60	2,69	2,78	2,87	2,97	3,09	2,2 1
7,7	2,20	2,36	2,43	2,54	2,62	2,72	2,81	2,91	3,01	2,16
7,8	2, 19	2,27	2,35	2,45	2,55	2,65	2, 74	2,84	2,92	2,09
7,9	2, 18	2,14	2,24	2,34	2,43	2,53	2,63	2,73	2,83	2,01
8,0	1, 17	2,03	2,12	2,21	2,31	2,40	2,49	2,64	2,72	1,85
8,1	1, 16	1,94	2,03	2,12	2,23	2,32	2,41	2,53	2,61	1,76
8,2	1, 15	1,82	1,92	2,00	2,11	2,19	2,30	2,39	2,48	1,65
8,3	1, 14	1,68	1,79	1,87	1,97	2,08	2,17	2,28	2,36	1,52
8,4	1, 13	1,61	1,70	1,78	1,89	1,97	2,08	2,17	2,27	1,43
8,5	1, 12	1,51	1,58	1,67	1,78	1,87	1,96	2,06	2,16	1,32
8,6	1, 11	1,35	1,45	1,54	1,66	1,73	1,83	1,94	2,04	1,18
8,7	1, 10	1,33	1,43	1,52	1,62	1,71	1,80	1,91	2,01	1,15
8,8	1,09	1,25	1,31	1,41	1,51	1,62	1,69	1,80	1,90	1,06
8,9	1,07	1,22	1,29	1,39	1,47	1,58	1,66	1,76	1,88	1,03
9,0	0,93	1,07	1,15	1,25	1,35	1,45	1,55	1,65	1,74	0,90
9,1	0,87	1,02	1, 14	1,22	1,29	1,38	1,47	1,58	1,67	0,84
9,2	0,8 6	0,95	1, 1 3	1,1 5	1,23	1,33	1,4 5	1,5 6	1,62	0,78
9,3	0,8 5	0,9 4	1, 12	1,1 4	1,19	1,27	1,4 4	1,5 5	1,6 1	0,7 7
9,4	0,8 4	0,9 3	1, 11	1,1 3	1,17	1,2 6	1,4 3	1,54	1,6 0	0,76
9,5	0,8 3	0,9 2	1, 1 0	1,12	1,1 6	1,2 5	1,4 2	1,5 3	1, 59	0,7 5
9,6	0,8 2	0,9 1	1,0 5	1,1 1	1,1 5	1,2 4	1,4 1	1,5 2	1, 58	0,7 4
9,7	0,8 1	0,9 0	1,0 4	1,09	1,1 4	1,2 3	1,38	1,5 0	1, 57	0,7 3
9,8	0,80	0,77	1,0 1	1,0 8	1,1 3	1,2 2	1,3 7	1,45	1, 56	0,7 2
9,9	0, 79	0,7 6	0,95	1,0 7	1,1 2	1, 15	1,3 6	1,4 4	1,55	0,7 1
10,0	0,73	0,7 5	0,9 3	1,0 6	1,1 1	1, 14	1,3 5	1,4 3	1,5 4	0,70

Таблица 2. Методы численного интегрирования

Предпоследняя цифра шифра	Метод определения пройденного пути	Предпоследняя цифра шифра	Метод определения пройденного пути
0	Метод левых прямоугольников	5	Метод правых прямоугольников
1	Метод трапеции	6	Метод левых прямоугольников
2	Метод правых прямоугольников	7	Метод трапеции
3	Метод левых прямоугольников	8	Метод правых прямоугольников
4	Метод трапеции	9	Метод левых прямоугольников

Приближение равнопеременного движения широко используется при описании динамики транспортных объектов. Его отличительной особенностью является линейный закон изменений скорости движения. На небольшом интервале наблюдений линейная модель служит хорошим приближением реальной более сложной функциональной зависимости скорости движения от времени. Линейное приближение позволяет оценивать параметры движения и прогнозировать динамику развития транспортных процессов.

Линейная модель изменений скорости движения объекта имеет вид

(1)

Коэффициенты модели и характеризуют скорость в момент времени и ускорение движения объекта, соответственно.

Оценки коэффициентов теоретической модели 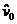, вычисляются по результатам наблюдений, представленных последовательностью значений скорости движения объекта в дискретные моменты времени . Их оптимальные значения определяются условиями минимума квадратичного функционала, представляющего собой сумму квадратов отклонений результатов наблюдений от принятой теоретической модели:

Условия равенства нулю производных , 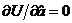приводят к системе линейных алгебраических уравнений для вычислений коэффициентов модели

(2)

где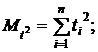

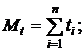
Выразим из выражения (2) a и b, получим:

(3)

Подставим в (1) полученные выражения для a и b из (3), при условии, что даны дискретные значения замеров скорости и времени и 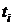соответственно. В итоге получаем линейную модель изменения скорости движения отцепа.

(4)

После того, как была получена модель изменения скорости движения отцепа (4), необходимо определить момент времени выключения замедлителей при условии заданной величины скорости на выходе из замедлителей . Для этого необходимо из выражения (4) выразить время 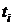, а вместо расчетного значения скорости 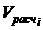, подставить заданную величину скорости на выходе из замедлителей, после чего получим:

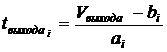
(5)

Из полученных значений необходимо выбрать одно, которое удовлетворяет условию (6):

(6)

В заключении необходимо определить путь пройденный отцепом, зная его зависимость изменения скорости от времени . Известно, что пройденный путь зависит от функции изменения скорости по следующему выражению:

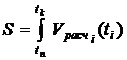
(6)

где и 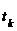- начало и конец интервала замера скорости соответственно.

ЗАДАНИЕ НА УЧЕБНУЮ ПРАКТИКУ

Данная работа выполняется в среде MathCad.

1) Вычислить расчётную скорость на выходе из замедлителей .;

2) Выполнить расчеты по полученной линейной модели изменения скорости движения отцепа и получить значения скорости ;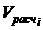

3) Построить график зависимости и полученных значений в ходе замеров (таблица 1);

4) Определить момент выхода отцепа из тормозной позиции посредством использования панели «Программирование»;

5) Определить пройденный отцепом путь методом из таблицы 2.

6) Построить графики в одной оси координат, который будет содержать следующие функции: , полученных значений в ходе замеров (таблица 1), и . Последнюю функцию построить при услови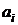и и 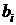где i = номеру замера, при котором выполняется условие (6).

Примерный вид графика, который должен получиться в пункте 6.

ФОРМЫ ОТЧЕТНОСТИ ПО ПРАКТИКЕ

Прохождение практики осуществляется студентом в соответствии с индивидуальным заданием, указанном в методических указаниях, выдаваемом руководителем практики от кафедры. Руководитель практики от кафедры отображает итоги прохождения практики в следующих документах:

- рецензии на отчет студента по практике;

- студенческой аттестационной книжке;

- зачетной ведомости;

- зачетной книжке.

Отчет является основным документом, характеризующим работу студента во время практики. В отчете должны быть отражены изученные во время практики общие вопросы и основные результаты практической деятельности студента в соответствии с рабочей программой практики и индивидуальным заданием, полученным студентом.

Отчет долен содержать:

1. Титульный лист;

2. Перечень и содержание выполненных работ (в соответствии с заданием) и индивидуальным планом.

3. Необходимы расчеты и пояснения к индивидуальному заданию.

Отчет по практике оформляется на листах формата А4 (210×297). Отчет должен быть набран на компьютере, используя шрифт типа Times New Roman, размер шрифта – 14, межстрочный интервал – 1,5 строки. Форматирование текста – по ширине, поля стандартные (левое – 2,5см, правое – 1,5см, верхнее и нижнее – 2см) Примерный объем отчета – 20-25 страниц машинописного текста.

Отчет должен сопровождаться необходимыми расчетами, таблицами и графиками.

ПРИЛОЖЕНИЕ

Аппроксимация функций.

Применение интерполяции позволяет получить функцию, совпадающую в узлах интерполяции с имеющимися эмпирическими данными, но часто такое совпадение может не означать совпадение характеров поведения исходной и интерполирующей функций на всем интервале наблюдения (например, из-за отклонений измеренных значений функции, ввиду погрешностей измерительной аппаратуры (сами значения являются приближенными) или влияния случайных факторов на процесс измерений).

Формулировка задачи аппроксимации выглядит следующим образом.

Пусть в результате измерений в процессе опыта получено табличное задание функции 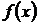, тогда необходимо найти функцию заданного вида 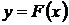, которая в точках принимает значения, как можно более близкие к табличным 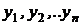. При такой формулировке задача аппроксимации функции одной переменной учитывает характер поведения функции на интервале наблюдений.

Практически вид приближающей функции чаще всего определяют путем сравнения приближенно построенного графика функции с графиками известных исследователю функций, заданных аналитически (как правило, элементарных функций) (рис.6).

Рис. 6

На рисунке 6 изображены три ситуации:

А) взаимосвязь 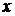и близка к линейной, прямая близка к точкам наблюдений, а последние отклоняются из-за небольших случайных воздействий;

Б) взаимосвязь величин 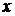и описывается нелинейной функцией, достаточно хорошо которую описывает ветка параболы;

В) явная взаимосвязь между переменными отсутствует, отклонение любой линии от точек будет велико.

Аппроксимация позволяет находить значения функции 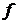для не табличных значений 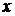, «сглаживая» результаты измерений величины .

Аппроксимация методом наименьших квадратов.

При данном методе в качестве критерия близости приближающей функции к исходной функции 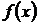используется минимум суммы квадратов разностей наблюдений зависимой переменной и теоретических, рассчитанных по уравнению регрессии значений : .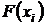

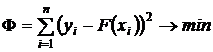Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами:

(10)

Сумма квадратов разностей соответствующих значений имеет вид:

Задача сводится к отысканию минимума функции трех переменных . Условие экстремума функции

Система уравнений для определения неизвестных параметров имеет вид:

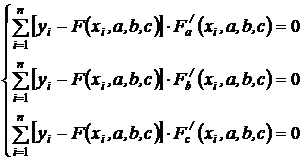(11)

Нахождение аппроксимирующей функции в виде основных элементарных функций.

А) линейная регрессия

Найдем частные производные: ,

Система уравнений имеет вид:

После преобразований и введения обозначений система уравнений приобретает вид:

Где , , ,

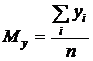Решив данную систему, получим значения параметров и

Численное интегрирование

При исследовании математических моделей часто возникает необходимость вычисления различного рода интегралов от соответствующих функций. Вместе с тем, применение формулы Ньютона-Лейбница реализовать на практике не всегда возможно, поскольку первообразная не всех функций может быть выражена через элементарные или другие известные функции. В этих случаях применяют методы приближенного интегрирования, позволяющими найти численное значение определенного интеграла приближенно с любой точностью.

Идея численного (приближенного) интегрирования вытекает из геометрического смысла определенного интеграла – значение определенного интеграла численно равно площади криволинейной трапеции, ограниченной графиком функции 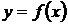, осью абсцисс и прямыми и . Площадь криволинейной трапеции и является значением интеграла.

Формально процедура численного интегрирования заключается в том, что отрезок разбивается на частичных отрезков, а затем подынтегральная функция заменяется на каждом отрезке легко интегрируемой функцией, интерполирующей значения подынтегральной функции в точках разбиения

Наиболее простыми методами численного интегрирования являются:

1. Метод прямоугольников;

2. Метод трапеций;

А) Метод прямоугольников.

Разобьем сегмент на равных между собой частей с помощью точек: 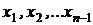. Тогда длина части (в последующем – шаг интегрирования) определяется как 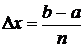. В этом случае аргумент любой промежуточной точки разбиения можно найти из соотношения . Тогда можно представить ординату подынтегральной функции в виде .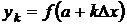

В этом случае суммы и будут интегральными для функции 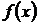на отрезке (при рассмотрении первой суммы в качестве значения функции на интервале 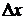рассматриваются левые концы частичных сегментов (элементарный прямоугольник строится по левому концу сегмента), а при составлении второй – правые (см.рис.8, 9)).

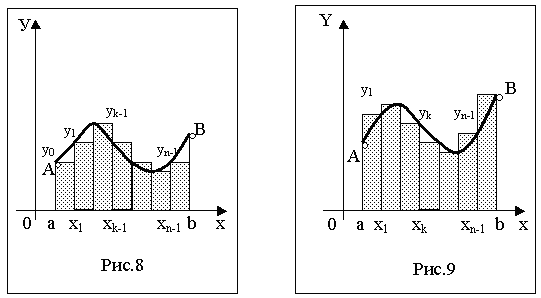
Окончательно формула прямоугольников имеет вид:

- для рис 8. (20)

- для рис. 9. (21)

Метод прямоугольников – это наиболее простой и грубый метод приближенного интегрирования. Заметно меньшую погрешность дает другой метод – метод трапеций.

Б) Метод трапеций.

Чем больше число отрезков разбиения, тем более точный результат дает метод прямоугольников. Больший интерес представляют методы, дающие более точные результаты без увеличения числа точек разбиения. Простейшая из таких формул получается, как среднее арифметическое правых частей формул (20) и (21).

(22)

Геометрический смысл формулы заключается в замене подынтегральной функции на каждом отрезке разбиения стягивающей хордой (линейная интерполяция) и вычислении площади полученной трапеции (рис. 10), равной

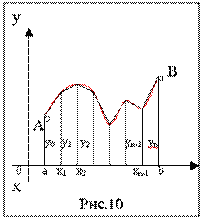
Приведя в формуле (22) подобные члены, окончательно получим формулу трапеций