Основные правила написания математических формул

 

2.4.1 При изложении выводов из математических формул не рекомендуется использовать выражения: «мы получили», «мы нашли», «определили», «получится», «выразится в виде», «будем иметь» и т. п. Следует употреблять слова: «получаем», «определяем», «находим», «преобразуем к виду» и т. д.

Связующие слова «следовательно», «откуда», «поскольку», «так как», «или» и другие располагают в начале строк, а знаки препинания ставят непосредственно за формулой. Например:

Характеристическое уравнение преобразуем к виду

.                                                         (*)

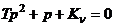Подставим в (*) значение

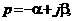
получим

,

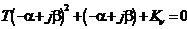откуда находим

,

.

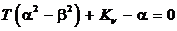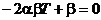Следовательно,

; .

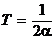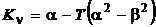Если формулам предшествует фраза с обобщающим словом, то после нее необходимо ставить двоеточие. Например:

Из равенства (2.12) находим следующее соотношение:

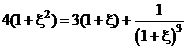 или .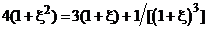

2.4.2 Математические формулы должны быть вписаны отчетливо с точным размещением знаков, цифр и букв. Каждую букву в формулах и тексте необходимо записывать в точном соответствии с алфавитом. Для того чтобы в формулах различать символы сходного начертания, принято буквы латинского алфавита печатать курсивом, а русского и греческого – прямым шрифтом. Образцы букв приведены в приложении Ф.

На протяжении всей пояснительной записки необходимо соблюдать следующие размеры в формулах: 3–4 мм для строчных и 6–8 мм для прописных букв и цифр. Все индексы и показатели степени должны быть в 1,5–2 раза меньше.

Знаки сложения, вычитания, корня, равенства и т. д. необходимо размещать так, чтобы их середина была расположена строго против горизонтальной черты дроби.

2.4.3 Формулы, как правило, располагают на отдельных строках по центру и отделяют от текста пробельными строками. В приложении М приведены примеры расположения формул с указанием расстояний между строками текста.

Рекомендуются следующие межтекстовые промежутки для размещения формул:

– 6 интервалов при печатном способе или 24 мм при рукописном для простейших однострочных формул;

– 8 интервалов при печатном способе или 32 мм при рукописном для однострочных формул, содержащих знаки Σ, Π, ∫ и  т. п.;

– для формул, содержащих две строки и более, а также для сложных выражений необходимо выставлять межтекстовые промежутки в соответствии с рекомендациями пунктов 2.4.2 и 2.4.3.

2.4.4 Короткие однотипные формулы допускается располагать на одной строке, разделяя точкой с запятой. Например:

Координаты x ₁ и x ₂ определяем по известным величинам X и Y:

 

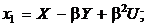
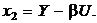
Несложные и короткие формулы промежуточных и вспомогательных выражений можно располагать непосредственно в строке текста. Причем разрешается увеличивать расстояние между строками текста. Например:

 

 

Так как добротность системы 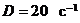, то на критической частоте  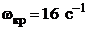коэффициент усиления разомкнутой системы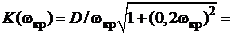 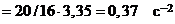. Следовательно, запас устойчивости по усилению .

 

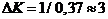2.4.5 При необходимости допускается перенос части математического выражения на следующую строку. Причем знак операции, на котором сделан перенос, пишут два раза – в конце первой и в начале второй строки. При переносе формулы на знаке умножения вместо «·» применяют знак «×».

Не допускаются переносы на знаке деления, а также выражений, относящихся к знакам корня, интеграла, логарифма, тригонометрических функций и т. п.

2.4.6 Все формулы, расположенные в отдельных строках, нумеруют. Одним номером отмечают также группу однотипных формул, размещенных на одной строке.

Формулы рекомендуется нумеровать в пределах раздела, к которому они относятся. Номер формулы должен состоять из порядкового номера раздела и отделенного от него точкой порядкового номера формулы, например формула (2.7). Если в разделе одна формула, ее также нумеруют, например формула (1.1).

Если в пояснительной записке формул не много, то разрешается применять сквозную нумерацию.

Формулы, помещаемые в приложения, должны иметь отдельную нумерацию в пределах каждого приложения. Вначале указывают обозначение приложения, затем ставят точку и приводят порядковый номер формулы в данном приложении, например (Б.2).

2.4.7 Порядковый номер формулы записывают арабскими цифрами в круглых скобках у правого края строки.

При переносе части формулы с одной строки на другую номер располагают на последней строке.

Номер сложной формулы (в виде дроби) записывают так, чтобы середина номера располагалась на уровне черты дроби.

Ссылки в тексте пояснительной записки на порядковый номер формулы следует приводить в круглых скобках с обязательным указанием слова «формула», «уравнение», «выражение», «равенство», «передаточная функция» и т. д. Например:

Подставляя выражение (3.6) в уравнение (3.2), получаем…

После формулы следует помещать перечень и расшифровку приведенных в формуле символов, которые не были пояснены ранее.

Перечень начинают со слова «где», которое приводят с новой строки без абзацного отступа; после слова «где» двоеточие не ставят. В этой же строке помещают первый поясняющий символ. Символы необходимо отделять от расшифровок знаком тире, выравнивая перечень по символам. Каждую расшифровку заканчивают точкой с запятой. Размерность символа или коэффициента указывают в конце расшифровки и отделяют запятой. Например:

 

При разгоне механизма до скорости быстрого хода двигатель должен развивать динамический момент M _дин, Hм, который определяем по формуле

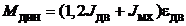,                                        (2.7)

где  1,2 – коэффициент, учитывающий приведенный момент инерции редуктора;

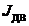   – момент инерции двигателя, кг·м²;

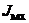 – приведенный к валу двигателя момент инерции механизма, кг·м²;

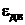  – ускорение вала двигателя, с^–2.

 

Иногда расшифровку символов и числовых коэффициентов начинают со слова «здесь». В этом случае после формулы ставят точку, а слово «здесь» записывают с абзацного отступа с прописной буквы. Например:

 

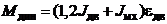.                                           (2.7)

Здесь 1,2 – коэффициент и т. д., как в предыдущем примере.

 

Разрешается расшифровку начинать с обобщающих слов, после которых следует ставить двоеточие, а каждый поясняемый символ начинать с красной строки. Например:

В формуле (2.7) обозначено:

1,2 – коэффициент, учитывающий… и т. д.