Раздел 16.1. Последовательности
Понятие последовательности как частного случая отображения.
Числовые последовательности
Предел последовательности. Сходящиеся и расходящиеся последовательности
Определение предела функции на языке последовательности
Функциональные последовательности
Раздел 16.2. Ряды
Последовательность частичных сумм. Определение ряда.
Числовые ряды. Примеры. Расходимость гармонического ряда
Необходимое условие сходимости ряда
Признаки сходимости
Функциональные ряды.
Ряд Тейлора
Разложение некоторых элементарных функций в ряд Тейлора
Формула Эйлера
Программные положения
В лекции рассматриваются понятия последовательности и ряда. Эти понятия необходимы будут при изучении 3 Модуля настоящего курса при рассмотрении законов распределений дискретных случайных величин (числовые), а также последовательностей случайных величин (функцинальные).
В лекции приводятся самые общие свойства рядов и некоторые признаки сходимости, для того, чтобы дать самые предварительные представления.
Разложение функции в ряд позволяет, в частности, находить приближенные ее значения со любой заданной точностью.
Завершается текст лекции формулой Эйлера, показывающей связь между «внешне» далекими разделами математики.
Методические рекомендации.
Обратите внимание на различия в определении последовательности и ряда. Рассмотрите определения сходимости последовательности и ряда, понятие суммы ряда. Уделите внимание функциональным последовательностям и рядам. Примите к сведению возможность разложения функции в ряд Тейлора. Конкретные формулы приводятся без доказательства, однако их можно без труда в любом из рекомендованных источников.
Вопросы для самоконтроля
1. Что такое последовательность?
2. Дайте определение сходящейся числовой последовательности
3. Дайте определение предела функции на языке последовательностей
4. Дайте определение ряда. Какой ряд называется числовым, функциональным? Приведите примеры
5. Сформулируйте признаки сходимости
6. Что такое ряд Тейлора?
7. Приведите примеры разложения элементарных функций в ряд Тейлора
8. Напишите формулу Эйлера
9. Исследуйте на сходимость последовательности:
10. Напишите формулу n-го члена ряда по неуказанным нескольким первым членам:

11. Напишите несколько первых членов ряда по указанной формуле n-го члена
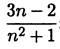
12. Исследуйте на сходимость ряды
1) Проверить необходимое условие сходимости

2) Признаки сравнения

4) Признак Деламбера

5) Радикальный признак Коши

3) Теорема Лейбница

Литература
А.В.Дорофеева «Высшая математика» Глава 5 § 5.7
А.В.Дорофеева «Высшая математика» Глава 12
Б.П.Демидович, В.А.Кудрявцев«Краткий курс высшей математики» Глава VII § 5
Б.П.Демидович, В.А.Кудрявцев«Краткий курс высшей математики» Глава XXI § 1-16
Дополнительно:
А.Я.Хинчин «8 лекций по математическому анализу, Лекция IV, «Ряды»)
Раздел 16.1. Числовые последовательности
Понятие последовательности как частного случая отображения.
Предел последовательности. Сходящиеся и расходящиеся последовательности
Определение предела функции на языке последовательности
Определение 16.1.1.
Под числовой последовательностью x1, x2, …, хn, … понимается функция xn = f(n), заданная на множестве натуральных чисел N ={1,2,3,…}, 
Числа x1, x2, …, хn, … называются членами последовательности:
x1 – первым членом, x2- вторым …, хn,- «энным» или общим членом последовательности
Формулы, позволяющие выразить n-й член последовательности через предыдущие члены, называются рекуррентными
Последовательность x1, x2, …, хn, … обычно обозначают как { хn }, и определяется она через свой общий член хn
Замечание 16.1.1
В общем случае (см. лекцию 9 «Отображения») последовательность является частным случаем отображения, которое не обязательно является функцией, то есть множество Y, куда отображается множество натуральных чисел N, может и не быть числовым. Примером могут быть, скажем, функциональные последовательности.
Примеры 16.1.1.
Написать первые четыре члена последовательности { xn }, если
1)

Подставляя поочередно n = 1,2,3 и 4, получим x1= -1, x2=1/2,x3 = - 1/3, x4 = 1/4
2) 
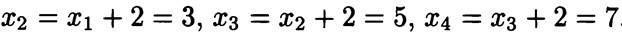
3) Рекуррентной формулой можно задать последовательность чисел Фибоначчи:
х1=х2 = 1, хn = хn-1 + хn-2  , названных по имени итальянского математика Леонардо Пизанского (Фибоначчи) (1180-1240), который способствовал проникновению в Европу достижений арабов в математике.
, названных по имени итальянского математика Леонардо Пизанского (Фибоначчи) (1180-1240), который способствовал проникновению в Европу достижений арабов в математике.
1, 1, 2, 3, 5, 8, 13, ….
Пример 16.1.2.
Написать формулу n члена последовательности хn

Поскольку
1=2∙ 1 – 1 при n=1; 3=2∙2 – 1 при n=2; 5 = 2 ∙3 – 1при n=3; 7 = 2∙4 – 1 при n =4
хn = 1/(2∙n – 1)
Определения 16.1.2.
Последовательность, все члены которой равны одному и тому же числу, называется постоянной
Пример 16.1.2. Формула n-го члена хn = 1 определяет последовательность 1, 1, 1, …, 1,…
Определение 16.1.3.
Пределом последовательности b (n = 1,2,…)
b = lim {xn } при n →∞
если для любого ε > 0 существует такое число N, зависящее от ε, что для всех натуральных n>N выполняется


Замечание 16.1.1. Строго говоря, нужно писать  , но поскольку n – натуральное число, то по смыслу
, но поскольку n – натуральное число, то по смыслу
 - одно и то же
- одно и то же
В общем случае N зависит от ε (что учтено в обозначении N (ε)). Как правило, чем меньше число ε, тем больше N.
Определение 16.1.4
Последовательность, для которой точка b ϵ R является пределом, называют сходящейся к этой точке. Определение по геометрическому смыслу означает, что какой бы малый интервал длины 2ε с центром в точке b ни взять на числовой прямой, все элементы последовательности {хn}) начиная с некоторого номера N + 1, должны попадать в этот интервал (рис. 1). Вне его будет только конечное число элементов последовательности.

Рис.1
Отсюда следует, что добавление к последовательности конечного числа элементов или исключение из нее конечного числа элементов не влияет на ее сходимость и значение ее предела, изменяется лишь номер, начиная с которого все элементы последовательности попадают в выбранную е-окрестность точки b.
Примеры 16.1.3.
1)Покажем, что 
При произвольном ε > О предположим, что |1/n - 0| < ε. Тогда
n > 1/ε. Если принять N = [1/ε] (целая часть числа 1/ε), то
наше утверждение будет верно по определению 16.1.5.
2) Последовательность
 = -1/2, 2/3, -3/4, 4/5,…не имеет предела, то есть
= -1/2, 2/3, -3/4, 4/5,…не имеет предела, то есть 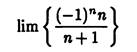 не существует
не существует
Действительно, если выбрать ε = 1, то все ее четные элементы попадают в ε-окрестность U(l, 1) точки х = 1, а все нечетные элементы — в ε-окрестность U(—1, 1) совсем иной точки х = — 1, причем эти окрестности не имеют общих точек (U(l, l) 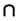 U(-l, 1) = 0) (см.рис. 2). А по определению 6.1.3 если бы одна из точек х = 1 или х = — 1 была пределом этой последовательности, то все ее элементы, начиная с некоторого номера, должны были попасть в выбранную окрестность этой точки.
U(-l, 1) = 0) (см.рис. 2). А по определению 6.1.3 если бы одна из точек х = 1 или х = — 1 была пределом этой последовательности, то все ее элементы, начиная с некоторого номера, должны были попасть в выбранную окрестность этой точки.

Рис.2.
Определение 16.1.5.
Точка а называется пределом значений функции  (или, короче, пределом функции f(x)), в точке х0 (или, что то же самое, при х —> х0), если для любой последовательности точек
(или, короче, пределом функции f(x)), в точке х0 (или, что то же самое, при х —> х0), если для любой последовательности точек  имеющих пределом x0, то есть такой, что
имеющих пределом x0, то есть такой, что  , последовательность {f(xn)} значений функции f в точках хn, n=1, 2, …, имеет свои пределом точку а:
, последовательность {f(xn)} значений функции f в точках хn, n=1, 2, …, имеет свои пределом точку а:

В этом случае пишут  ,
,
В символической записи это определение выглядит следующим образом:
 <═>
<═> 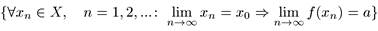
Если в этой формуле а существует, то говорят, что в точке х функция f(x) имеет конечный предел а.
Примеры 16.1.4.
1) Рассмотрим функцию  определенную на множестве R\{1} и выясним, существует ли предел этой функции при х, стремящемся к нулю,
определенную на множестве R\{1} и выясним, существует ли предел этой функции при х, стремящемся к нулю,  .
.
Пусть
 тогда
тогда
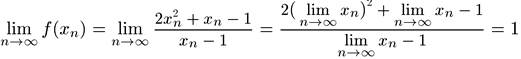
Таким образом, существует предел

А поскольку он не зависит от выбора последовательности, существует и
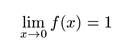
2) Рассмотрим функцию  , определенную на множестве R\{0}.
, определенную на множестве R\{0}.
Выясним, существует ли предел 
Рассмотрим последовательности  n = 1, 2, …. Очевидно, что
n = 1, 2, …. Очевидно, что 
 , n = 1, 2, 3, …
, n = 1, 2, 3, …
Поэтому
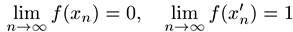 ,
,
а это означает, что у рассматриваемой функции нет предела в
точке х0 = 0.

Рис.3
Рассмотрим теперь понятие функциональной последовательности
Определение 16.1.6.
Пусть  , — некоторое множество действительных или комплексных функций м(х), определенных на множестве
, — некоторое множество действительных или комплексных функций м(х), определенных на множестве  . Тогда последовательность элементов множества U, т.е. всякое отображение множества натуральных чисел N в множество U, при котором каждому номеру
. Тогда последовательность элементов множества U, т.е. всякое отображение множества натуральных чисел N в множество U, при котором каждому номеру  ставится в соответствие некоторая функция
ставится в соответствие некоторая функция  , называют функциональной последовательностью (или последовательностью функций) и обозначают
, называют функциональной последовательностью (или последовательностью функций) и обозначают
 Множество X при этом называют областью определения
Множество X при этом называют областью определения
функциональной последовательности 
функции 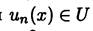 — членами (элементами) функциональной
— членами (элементами) функциональной
последовательности 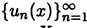 .
.
Определение 16.1.7.
При фиксированном  всякой функциональной
всякой функциональной
последовательности  , соответствует числовая
, соответствует числовая
(действительная или комплексная) последовательность 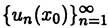 , элементами которой являются значения
, элементами которой являются значения  функций
функций  в точке x0.
в точке x0.
Определение 16.1.8.
Заданную на множестве 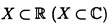 функциональную последовательность
функциональную последовательность 
называют сходящейся в точке  , если сходится числовая
, если сходится числовая
последовательность  . В противном случае,
. В противном случае,
функциональную последовательность  называют
называют
расходящейся в точке x0.
Если последовательность  , сходится в
, сходится в
каждой точке некоторого множества  , то эту
, то эту
функциональную последовательность называют сходящейся на
множестве М. Множество  всех точек
всех точек  , в
, в
которых последовательность  , определенная на X,
, определенная на X,
сходится, называют областью сходимости функциональной последовательности  .
.
Если функциональная последовательность 
сходится на множестве  , то всякой точке
, то всякой точке  можно
можно
поставить в соответствие предел числовой последовательности
значений функций  в этой точке. Таким образом, если
в этой точке. Таким образом, если
последовательность  сходится на множестве М, то на М определена некоторая функция
сходится на множестве М, то на М определена некоторая функция

В соответствии с определением предела числовой последовательности (16.1.1) можно сформулировать эквивалентное
Определение деление поточечной сходимости функциональной 16.1.9. последовательности 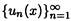 к функции u(х) на множестве М:
к функции u(х) на множестве М:
 Замечание 16.1.2.
Замечание 16.1.2.
Номер  зависит и от элемента
зависит и от элемента  , и от числа
, и от числа 
Замечание 16.1.3.
Если из контекста ясно, о какой области определения X идет речь, функциональные последовательности
 , обозначаются просто
, обозначаются просто  .
.
Пример 16.1.5.
Рассмотрим функциональную последовательность  , определенную на множестве X = [0,1]
, определенную на множестве X = [0,1]
следующим образом:

Покажем, что эта последовательность сходится во всей области
определения X = [0,1], и ее предельной функцией является
функция u(х) = 0.
Действительно,

(множитель х, не зависящий от n, вынесен за знак предела).
Пример 16.1.6.
Рассмотрим последовательность функций  , определенных на множестве
, определенных на множестве  . Для всех
. Для всех  получаем
получаем

а при  последовательность
последовательность  не имеет предела. Таким образом, областью сходимости функциональной
не имеет предела. Таким образом, областью сходимости функциональной
последовательности  является множество
является множество 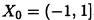 , на
, на
котором эта последовательность сходится поточечно к функции u(х), равной нулю во всех точках  и равной
и равной
единице в точке х = 1.
Раздел 16.2. Ряды
Последовательность частичных сумм. Определение ряда.
Числовые ряды. Признаки сходимости. Примеры. Расходимость гармонического ряда
Функциональные ряды.
Ряд Тейлора
Разложение некоторых элементарных функций в ряд Тейлора
Формула Эйлера
«… орудие это (теория рядов) вполне заслуживает того, чтобы даже в нашем кратком курсе ему была посвящена особая лекция; и не столько потому, что многочисленными применениями ее проникнуто все здание как самого анализа, так и почти всех опирающихся на него прикладных наук, сколько по той причине, что на сравнительно несложном материале, какой представляет собой теория рядов, типичные для всего анализа ходы мыслей, цепи представлений и образов и даже целые логические схемы выступают в теории рядов с особенностью и рельефностью; хорошо известно, что учащемуся, который активно и прочно овладел теорией рядов, дальнейшее усвоение основных разделов анализа обычно не доставляет никаких затруднений»
(А.Я.Хинчин «8 лекций по математическому анализу, Лекция IV, «Ряды»)
Понятие бесконечных сумм фактически было известно ученым Древней Греции (Евдокс, Евклид, Архимед). Нахождение бесконечных сумм являлось составной частью так называемого метода исчерпывания, широко используемого древнегреческими учеными для нахождения площадей фигур, объемов тел, длин кривых и т.д. Так, например, Архимед для вычисления площади
параболического сегмента (т.е. фигуры, ограниченной прямой и параболой) нашел сумму бесконечной геометрической прогрессии со знаменателем 1/4. Ряд, как самостоятельное понятие, математики стали использовать в XVII в. И. Ньютон и Г. Лейбниц применяли ряды для решения алгебраических и дифференциальных уравнений. Теория рядов в XVIII-XIX вв. развивалась в работах Я. и И. Бернулли, Б. Тейлора, К. Маклорена, Л. Эйлера, Ж. Даламбера, Ж. Лагранжа и др. Строгая теория рядов была создана в XIX в. на основе понятия предела в трудах К. Гаусса, Б. Больцано, О. Коши, П. Дирихле, Н. Абеля, К. Вейерштрасса, Б. Римана и др.
Определение 16.2.1.
Пара последовательностей {un }, {sn}, где
 n = 1,2, …
n = 1,2, …
называется рядом или бесконечной суммой и обозначается
 или
или 
Определения 16.2.2.
Элементы последовательности {un } называются членами ряда, а элементы последовательности {sn} - его частичными суммами.

Определения 16.2.3.
Если существует конечный предел  , он называется суммой ряда. В этом случае ряд называется сходящимся и пишут
, он называется суммой ряда. В этом случае ряд называется сходящимся и пишут 
Определение 16.2.4.
Если последовательность частичных сумм не стремится к конечному пределу, то ряд называется расходящимся.
Очевидно, что u1 = s1, un = sn – sn-1, n =2,3,…
Из этих двух формул видно, что каждая из последователь-
ностей {un } и {sn} однозначно определяет другую. Таким образом,
чтобы задать ряд  , достаточно задать одну из последовательностей {un } или {sn}. В этом смысле изучение рядов равносильно изучению последовательностей.
, достаточно задать одну из последовательностей {un } или {sn}. В этом смысле изучение рядов равносильно изучению последовательностей.
Часто нумерацию членов ряда производят не натуральными
числами, а целыми, начиная с нуля, т. е. числами 0,1,2,..., а иногда — начиная с некоторого целого n0, т. е. числами n0,n0 + 1,...
Замечание 16.2.1.
Объединяя под термином «расходящиеся» как ряды с бесконечными суммами, так и ряды, не имеющие сумм, не имеют ничего общего и объединяются в одну группу в противовес понятию ряда с конечными суммами
Приведем здесь комментарий о бесконечных суммах из классической книги А.Я.Хинчина «8 лекций по математическому анализу, Лекция IV, «Ряды»




Примеры 16.2.1
1) примером сходящегося ряда является бесконечно убывающая геометрическая прогрессия  , | q|<1 (согласно определению, данный ряд - это две последовательности: собственно члены ряда: 1, q, q2, q3, q4,…, qn,… и последовательность частичных сумм: 1, 1+q, 1+q+q2, 1+q+q2 +q3, 1+q+q2 +q3 +q4,…, 1+q+q2 +q3 +q4 +…qn +…
, | q|<1 (согласно определению, данный ряд - это две последовательности: собственно члены ряда: 1, q, q2, q3, q4,…, qn,… и последовательность частичных сумм: 1, 1+q, 1+q+q2, 1+q+q2 +q3, 1+q+q2 +q3 +q4,…, 1+q+q2 +q3 +q4 +…qn +…
u = qn, n = 0,1,2,…
Sn = 
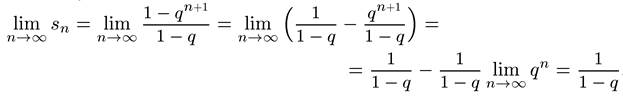
2) Примером расходящегося ряда может служить ряд с членами, равными единице, un= 1,  и
и  .
.
3) Ряд а – а + а – а + а – а +… (можно рассматривать, как геометрическую прогрессию со знаменателем (–1)
Величина Sn будет равна нулю или а в зависимости от того, будет ли n четно или нечетно. Ясно, что при а ≠ 0 не стремится ни к какому пределу при неограниченном возрастании n. Соответственно, данный ряд расходится.
4) Покажем, что является расходящимся гармонический ряд

Оценим величины частичных сумм с номерами 



Аналогично 
Соответственно, для любого натурального k выполняется

Таким образом, частичные суммы гармонического ряда при достаточно большом n могут иметь значения, большие любого наперед заданного числа. Следовательно:
 и, соответственно, гармонический ряд расходится.
и, соответственно, гармонический ряд расходится.
Теорема 16.2.1 (необходимое условие сходимости ряда). Если ряд
сходится, то последовательность его членов стремится к нулю.
Доказательство
Если ряд  сходится, т. е. существует конечный предел
сходится, т. е. существует конечный предел
 его частичных сумм, то из равенства
его частичных сумм, то из равенства
 следует, что
следует, что

Замечание 16.2.2
Это необходимое, но недостаточное условие. Контрпримером может служить так называемый гармонический ряд { 1/n } (Пример 16.2.1(4)).
В то же время теорему можно рассматривать как достаточное условие расходимости:
если  , то ряд расходится
, то ряд расходится
Пример 16.2.2
Рассмотрим на предмет сходимости ряд 
Проверим необходимое условие сходимости:

Поэтому ряд расходится, а так как все члены ряда положительны, он расходится к +∞.
Примером расходящегося ряда может служить также геометрическая прогрессия {qn } со знаменателем |q|>1
Рассмотрим теперь так называемые знакоположительные ряды (ряды, все члены которых положительны)
Признаки сравнения рядов с положительными членами:
1) Если члены ряда  положительны, то последовательность его частичных сумм Sn монотонно возрастает. Следовательно для сходимости знакоположительного ряда необходима и достаточна ограниченность последовательности {Sn}, nϵ N
положительны, то последовательность его частичных сумм Sn монотонно возрастает. Следовательно для сходимости знакоположительного ряда необходима и достаточна ограниченность последовательности {Sn}, nϵ N
2) Пусть  (А) и
(А) и  (В) – два ряда с положительными членами. Тогда справедлива
(В) – два ряда с положительными членами. Тогда справедлива
Теорема 16.2.2 (без доказательства ):
Предположим, что неравенство  - константа) выполняются при всех значениях n, начиная с некоторого номера n0. Тогда
- константа) выполняются при всех значениях n, начиная с некоторого номера n0. Тогда
1. Из сходимости ряда В следует сходимость ряда А
2. Из расходимости А следует расходимость В
Теорема 16.2.3 (без доказательства)
 Тогда ряды А и В сходятся и расходятся одновременно.
Тогда ряды А и В сходятся и расходятся одновременно.
Две последние теоремы предполагают, что для исследования сходимости ряда для сравнения необходим некий эталон. Часто для этих целей использую известные ряды:
1) сходящуюся бесконечно убывающую геометрическую прогрессию

2) ряд Дирихле  , сходящийся при р>1 и расходящийся при р ≤ 1
, сходящийся при р>1 и расходящийся при р ≤ 1
3) гармонический ряд 1 + ½ + 1/3 + … + 1/n + …
Пример 16.2.3.
Рассмотрим ряд 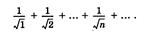 Так как
Так как 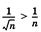 то, из сравнения с гармоническим рядом следует расходимость ряда
то, из сравнения с гармоническим рядом следует расходимость ряда
Рассмотрим без доказательства два признака сходимости знако- положительных рядов:
Теорема 16.2.2. Признак Даламбера (без доказательства)
Допустим, 
Тогда:
Если q<1 ряд сходится
q> 1 ряд расходится
q = 1 случай требует дополнительного рассмотрения, так как в этом случае ряд может как сходиться, так и расходиться
Пример
Рассмотрим ряд  , a>0
, a>0


На основании признака Даламбера при 0<a<1 ряд сходится, при a>1 – расходится.
При а = 1 признак ответа не дает, но ряд принимает вид:
 , а это гармонический ряд
, а это гармонический ряд
Теорема 16.2.3. Признак Коши радикальный (без доказательства)
Допустим 
Тогда:
Если q<1 ряд сходится
q> 1 ряд расходится
q = 1 случай требует дополнительного рассмотрения, так как в этом случае ряд может как сходиться, так и расходиться
Пример
Рассмотрим ряд  .
.
Применим радикальный признак Коши:

Ряд сходится.
Определение 16.2.5
Знакочередующимся (знакопеременным) рядом называется ряд вида 
где 
Иначе говоря, знакочередующимся называется ряд, у которого любые два рядом стоящих члена имеют разные знаки






