Лабораторная работа № 2
ПРОВЕРКА ПАРАМЕТРИЧЕСКИХ СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Цель работы: ознакомиться с методикой проведения проверки параметрических гипотез.
Задание: По выборке из лабораторной работы № 1 и заданному значению математического ожидания провести проверку гипотезы Н0 о равенстве математического ожидания заданному значению против предложенного вида альтернативной гипотезы На:
Н 0: 
= 
;
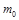На: ≠ .
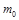В данном случае критерием для проверки нулевой гипотезы является случайная величина
(2.1)
Доказано, что если гипотеза Н0 верна, то с.в. t имеет распределение Стьюдента с ν = n – 1 степенями свободы.
Алгоритм проверки гипотезы Н0 следующий:
• по формуле (2.1) вычисляется значение критерия t;
• в таблице (Приложение А) по заданному уровню значимости α и числу степеней свободы ν = n – 1 находят критическую точку 
распределения Стьюдента;
• если
– < t < ,
то считается, что нет оснований для отклонения гипотезы Н0.
Если же
t ≤ – или t ≥ ,
то нулевая гипотеза отклоняется в пользу альтернативной.
Пример выполнения лабораторной работы
При проведении экспериментов фиксировались значения случайной величины X, характеризующей стоимость строительно-монтажных работ на участке, у.е.. В результате расчетов в Лабораторной работе № 1 подсчитано, что выборочное среднее значение равно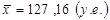 
, а выборочное среднее квадратическое отклонение этого параметра 
.
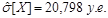Можно ли на основании имеющихся данных утверждать, что стоимость строительно-монтажных работ на участке, у.е в среднем составляет 
?
Решение.
Требуется на заданном уровне значимости α проверить гипотезу Н0 при альтернативе На:
Н0: = ;
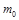На: ≠ .
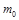Вычислим значение критерия t по формуле (3.1)
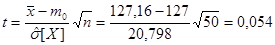
В таблице Г.3 найдем критическую точку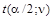 
распределения Стьюдента при уровне значимости α = 0,05 и числе степеней свободы 
, t(0,025; 49) = 2,0095. Поскольку выполняется неравенство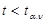 
, т.е. 
, то имеющиеся статистические данные не дают основания для отклонения нулевой гипотезы.
То есть можно считать, что стоимость строительно-монтажных работ на участке в среднем составляет 127 у.е.
Задание на выполнение работы
Решить задачу по варианту. Решение должно быть выполнено по алгоритму:
• сформулировать случайную величину (величины), которая будет исследоваться в задаче;
• указать, подчиняется ли исследуемая случайная величина (величины) нормальному закону распределения;
• записать (найти) оценки параметров исследуемой случайной величины (величин);
• сформулировать нулевую и альтернативную гипотезы;
• записать формулу для вычисления статистического критерия, который будет использоваться для проверки выдвинутой нулевой гипотезы;
• выполнить необходимые вычисления и сделать вывод о принятии или отклонении нулевой гипотезы;
• ответить на вопрос, сформулированный в задаче.
Распределение вариантов заданий
| Первая буква фамилии студента | Вес железобетонных перекрытий кг/м кв А-Д | Длина плиты перекрытия, м Е-Л | Время установки окон ПВХ, час. М-Т | Стоимость строительно-монтажных работ на участке, млрд р. У-Я |
| Задача | 30,5 | 4,2 | 70,4 |
Порядок выполнения работы
1 Изучить теоретические сведения.
2 Записать на диск выборку случайной величины, которую требуется исследовать.
3 По этой выборке и заданному значению математического ожидания провести проверку гипотезы о равенстве математического ожидания заданному значению против предложенного вида альтернативной гипотезы:
– вручную рассчитать значение выборочной статистики и сравнить его с критическим значением;
– с помощь процедуры «One-Sample Analysis» пакета Statgrafics.
5 Сделать выводы.
Контрольные вопросы
1 Что называется статистической гипотезой?
2 Дайте определение параметрической и непараметрической статистических гипотез.
3 Что такое нулевая и альтернативная гипотезы?
4 Что называется статистическим критерием?
5 Что называется уровнем значимости статистического критерия?
6 Что называется областью допустимых значений статистического критерия?
7 Сформулируйте правило принятия решения на основании выборочного значения статистического критерия.
ПРИЛОЖЕНИЕ А (справочное) Критические точки распределения Стьюдента
| Степени свободы n | Уровень значимости a (односторонняя критическая область) | |||||||
| 0.2 | 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | 0.0005 | |
| 1.376 | 3.078 | 6.314 | 12.706 | 31.821 | 63.656 | 318.29 | 636.58 | |
| 1.061 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 22.328 | 31.600 | |
| 0.978 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 10.214 | 12.924 | |
| 0.941 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 7.173 | 8.610 | |
| 0.920 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 5.894 | 6.869 | |
| 0.906 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 5.208 | 5.959 | |
| 0.896 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.785 | 5.408 | |
| 0.889 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 4.501 | 5.041 | |
| 0.883 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 4.297 | 4.781 | |
| 0.879 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 4.144 | 4.587 | |
| 0.876 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 4.025 | 4.437 | |
| 0.873 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.930 | 4.318 | |
| 0.870 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.852 | 4.221 | |
| 0.868 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.787 | 4.140 | |
| 0.866 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.733 | 4.073 | |
| 0.865 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.686 | 4.015 | |
| 0.863 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.646 | 3.965 | |
| 0.862 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.610 | 3.922 | |
| 0.861 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.579 | 3.883 | |
| 0.860 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.552 | 3.850 | |
| 0.859 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.527 | 3.819 | |
| 0.858 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.505 | 3.792 | |
| 0.858 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.485 | 3.768 | |
| 0.857 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.467 | 3.745 | |
| 0.856 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.450 | 3.725 | |
| 0.856 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.435 | 3.707 | |
| 0.855 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.421 | 3.689 | |
| 0.855 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.408 | 3.674 | |
| 0.854 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.396 | 3.660 | |
| 0.854 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.385 | 3.646 | |
| 0.851 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 3.307 | 3.551 | |
| 0.849 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 3.261 | 3.496 | |
| 0.848 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 3.232 | 3.460 | |
| 0.847 | 1.294 | 1.667 | 1.994 | 2.381 | 2.648 | 3.211 | 3.435 | |
| 0.846 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 3.195 | 3.416 | |
| 0.846 | 1.291 | 1.662 | 1.987 | 2.368 | 2.632 | 3.183 | 3.402 | |
| 0.845 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 3.174 | 3.390 | |
| 0.844 | 1.287 | 1.655 | 1.976 | 2.351 | 2.609 | 3.145 | 3.357 | |
| 0.843 | 1.286 | 1.653 | 1.972 | 2.345 | 2.601 | 3.131 | 3.340 | |
| 0.842 | 1.283 | 1.648 | 1.965 | 2.334 | 2.586 | 3.107 | 3.310 | |
| ¥ | 0.842 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 3.090 | 3.290 |
| Степени свободы | 0.4 | 0.2 | 0.1 | 0.05 | 0.02 | 0.01 | 0.002 | 0.001 |
| n | Уровень значимости a (двусторонняя критическая область) |
