Контрольная работа
дисциплины «Дополнительные главы математики»,
направления 13.03.02 (ЭО)
Вариант 1
Задача 1
Две грузовых машины могут подойти на погрузку в промежуток времени от 
9 часов до 
10 часов. Погрузка первой машины длится 
10 минут, второй – 
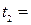10 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Задача 2
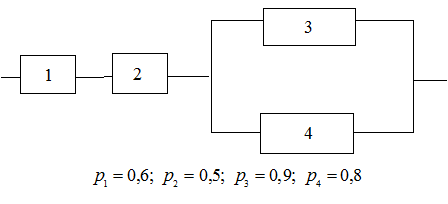
Определить надёжность схемы, представленной на рисунке, где 
- вероятность безотказной работы i-того элемента.
Задача 3
Среди поступивших на сборку деталей 30% - с завода №1, остальные – с завода №2. Вероятность брака для завода №1 равна 0,02, для завода №2 – 0,03. Найти а) вероятность того, что наугад взятая деталь стандартная; б) вероятность изготовления наугад взятой детали на заводе №1, если она оказалась стандартной.
Задача 4
Всхожесть семян некоторого растения составляет 80%. Посеяно шесть семян. Найти а) наивероятнейшее число взошедших семян и соответствующую ему вероятность; б) вероятность того, что взойдёт не менее пяти семян; в) вероятность того, что взойдёт не более одного семечка; г) вероятность того, что взойдёт хотя бы одно семечко.
Вариант 2
Задача 1
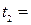Две грузовых машины могут подойти на погрузку в промежуток времени от 9 часов до 11 часов. Погрузка первой машины длится 10 минут, второй – 20 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Задача 2
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i-того элемента.
Задача 3
Заготовка может поступить для обработки на один из двух станков с вероятностями 0,4 и 0,6 соответственно. При обработке на первом станке вероятность брака составляет 2%, на втором – 3%. Найти вероятность того, что наугад взятое после обработки изделие – стандартное; б) наугад взятое после обработки стандартное изделие обработано на первом станке.
Задача 4
Вероятность работы каждого из семи моторов в данный момент равна 0,8. Найти а) наивероятнейшее число работающих моторов и соответствующую ему вероятность; б) вероятность того, что работает не менее шести моторов; в) вероятность того, что работает не более одного мотора; г) вероятность того, что работает хотя бы один мотор.
Вариант 3
Задача 1
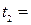Две грузовых машины могут подойти на погрузку в промежуток времени от 10 часов до 11 часов. Погрузка первой машины длится 10 минут, второй – 10 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Задача 2
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i-того элемента.
Задача 3
В дисплейном классе имеется 10 персональных компьютеров первого типа и 15 второго типа. Вероятность того, что за время работы на компьютере первого типа не произойдёт сбоя, равна 0,9, а на компьютере второго типа – 0,7. Найти вероятность того, что а) на случайно выбранном компьютере за время работы не произойдёт сбоя; б) компьютер, во время работы на котором не произошло сбоя – первого типа.
Задача 4
Оптовая база обслуживает шесть магазинов. Вероятность получения заявки базой на данный день для каждого из магазинов равна 0,6. Найти а) наивероятнейшее число заявок и соответствующую ему вероятность; б) вероятность того, что заявок будет не менее пяти; в) вероятность того, что заявок будет не более одной; г) вероятность того, что поступит хотя бы одна заявка.
Вариант 4
Задача 1
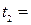Две грузовых машины могут подойти на погрузку в промежуток времени от 10 часов до 12 часов. Погрузка первой машины длится 10 минут, второй – 20 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Задача 2
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i-того элемента.
Задача 3
По линии связи передано два сигнала типов А и В с вероятностями соответственно 0,8 и 0,2. В среднем принимается 60% сигналов типа А и 70% типа В. Найти вероятность того, что а) посланный сигнал будет принят; б) принятый сигнал – типа А.
Задача 4
Продукция, поступающая из цеха в ОТК, не удовлетворяет условиям стандарта в среднем в 8% случаев. Найти а) наивероятнейшее число нестандартных среди семи случайно взятых изделий и соответствующую ему вероятность; б) вероятность того, что нестандартных изделий будет не менее шести; в) вероятность того, что нестандартных изделий будет не более одного; г) будет хотя бы одно нестандартное изделии.
Вариант 5
Задача 1
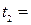Две грузовых машины могут подойти на погрузку в промежуток времени от 11 часов до 12 часов. Погрузка первой машины длится 10 минут, второй – 15 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Задача 2
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i-того элемента.
Задача 3
Для сигнализации о том, что режим работы автоматической линии отклоняется от нормального, используются индикаторы двух типов. Вероятности того, что индикатор принадлежит к одному из двух типов, равны соответственно 0,4 и 0,6. При нарушении работы линии вероятность срабатывания индикатора первого типа равна 0,9, второго – 0,7. а) Найти вероятность того, что наугад выбранный индикатор сработает при нарушении нормальной работы линии. б) Индикатор сработал. К какому типу он вероятнее всего принадлежит?
Задача 4
Вероятность того, что изделие пройдёт контроль качества, равна 0,8. Найти а) наивероятнейшее число изделий, прошедших контроль, из шести случайно отобранных изделий, и соответствующую ему вероятность; б) вероятность того, что контроль пройдёт не менее пяти изделий; в) вероятность того, что контроль пройдёт не более одного изделия; г) вероятность того, что контроль пройдёт хотя бы одно изделие.
Вариант 6
Задача 1
Две грузовых машины могут подойти на погрузку в промежуток времени от 11 часов до 13 часов. Погрузка первой машины длится 10 минут, второй – 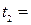15 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Задача 2
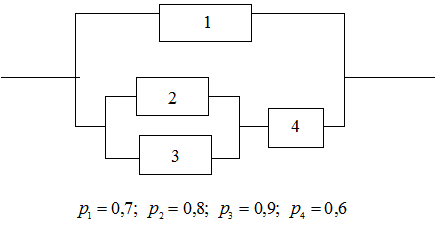
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i-того элемента.
Задача 3
Резистор, поставленный в телевизор, может принадлежать к одной из двух партий с вероятностями 0,6 и 0,4. Вероятности того, что резистор проработает гарантийное число часов, для этих партий соответственно равны 0,8 и 0,7. а) Найти вероятность того, что взятый наугад резистор проработает гарантийное число часов. б) Резистор проработал гарантийное число часов. К какой партии он вероятнее всего принадлежит?
Задача 4
Среди деталей, изготавливаемых рабочим, в среднем 2% нестандартных. Рабочий изготовил 20 деталей. Найти а) наивероятнейшее число стандартных деталей и соответствующую ему вероятность; б) вероятность того, что стандартных деталей будет не менее 19; в) вероятность того, что стандартных деталей будет не более одной; в) вероятность того, что будет хотя бы одна стандартная деталь.
Вариант 7
Задача 1
Две грузовых машины могут подойти на погрузку в промежуток времени от 9 часов до 9.30 часов. Погрузка первой машины длится 10 минут, второй – 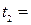10 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Задача 2
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i-того элемента.
Задача 3
Для участия в студенческих спортивных соревнованиях выделено 10 человек из первой группы и 8 из второй. Вероятность того, что студент первой группы попадёт в сборную вуза, равна 0,8, а для студента второй группы – 0,7. а) Найти вероятность того, случайно выбранный студент попал в сборную вуза. б) Студент попал в сборную вуза. В какой группе он вероятнее всего учится?
Задача 4
Вероятность поражения цели при одном выстреле равна 0,8. Произведено 7 выстрелов. Найти а) наивероятнейшее число попаданий и соответствующую ему вероятность; б) вероятность того, что будет не менее 6 попаданий; в) вероятность того, что будет не более одного попадания; г) вероятность хотя бы одного попадания.
Вариант 8
Задача 1
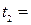Две грузовых машины могут подойти на погрузку в промежуток времени от 9 часов до 11.30 часов. Погрузка первой машины длится 10 минут, второй – 20 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Задача 2
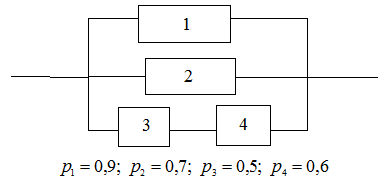
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i-того элемента.
Задача 3
В двух коробках имеются однотипные конденсаторы. В первой 20 конденсаторов, из них 2 неисправных, во второй – 10, из них 3 неисправных. а) Найти вероятность того, наугад взятый конденсатор из случайно выбранной коробки годен к использованию. б) Наугад взятый конденсатор оказался годным. Из какой коробки он вероятнее всего взят?
Задача 4
Вероятность потопить судно одной торпедой равна 0,2. Выпущено 5 торпед. Найти а) наивероятнейшее число попаданий и соответствующую ему вероятность; б) вероятность того, что будет не менее 4 попаданий; в) вероятность того, что будет не более одного попадания; г) вероятность хотя бы одного попадания.
Вариант 9
Задача 1
Две грузовых машины могут подойти на погрузку в промежуток времени от 10 часов до 10.30 часов. Погрузка первой машины длится 10 минут, второй – 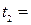15 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Задача 2
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i-того элемента.
Задача 3
Для поисков спускаемого аппарата космического корабля выделено 4 вертолёта первого типа и 6 вертолётов второго типа. Каждый вертолёт первого типа обнаруживает находящийся в районе поиска аппарат с вероятностью 0,6, второго типа – с вероятностью 0,7. а) Найти вероятность того, что наугад выбранный вертолёт обнаружит аппарат. б) К какому типу вероятнее всего принадлежит вертолёт, обнаруживший спускаемый аппарат?
Задача 4
Вероятность поражения мишени при одном выстреле равна 0,6. Произведено 5 выстрелов. Найти а) наивероятнейшее число попаданий и соответствующую ему вероятность; б) вероятность того, что будет не менее 4 попаданий; в) вероятность того, что будет не более одного попадания; г) вероятность хотя бы одного попадания.
Вариант 10
Задача 1
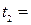Две грузовых машины могут подойти на погрузку в промежуток времени от 10 часов до 11.30 часов. Погрузка первой машины длится 10 минут, второй – 15 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
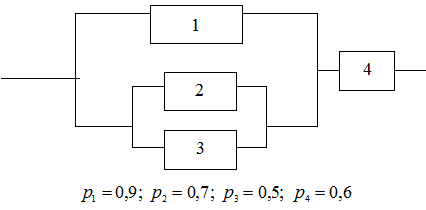Задача 2
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i-того элемента.
Задача 3
Пассажир может обратиться за получением билета в одну из трёх касс вокзала А или в одну из трёх касс вокзала В. Вероятность того, что к моменту прихода пассажира в кассах вокзала А имеются в продаже билеты, равна 0,6, в кассах вокзала В – 0,5. а) Найти вероятность того, в наугад выбранной кассе имеется в продаже билет. б) Пассажир купил билет. В кассе какого вокзала он вероятнее всего куплен?
Задача 4
Вероятность выиграть по одной облигации государственного займа равна 1/3. Некто купил 6 облигаций. Найти а) наивероятнейшее число выигравших облигаций и соответствующую ему вероятность; б) вероятность того, что выиграет не менее 5 облигаций; в) вероятность того, что будет не более одного выигрыша; г) вероятность хотя бы одного выигрыша.
Пример решения контрольной работы
Задача 1
Две грузовых машины могут подойти на погрузку в промежуток времени от 17 часов до 18.30. Погрузка первой машины длится 10 минут, второй – 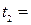5 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Решение
Пусть первая машина подошла на погрузку через x минут после 17 часов, а вторая – через y минут. Тогда время прибытия машин можно изобразить точкой на координатной плоскости. Так как обе координаты могут принимать значения от 0 до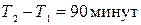 
, то все возможные исходы данного опыта будут представлены точками квадрата со стороной, равной 90 минут.
Исходы, благоприятствующие искомому событию А – одной из машин придётся ожидать окончания погрузки другой, изобразятся точками той части квадрата, которые являются решением системы неравенств:
Чтобы изобразить указанную область нарисуем прямые 
и 
. Для удобства уравнения этих прямых можно преобразовать к виду: 
и 
. Первая прямая проходит через точки (10; 0) и (90; 80). Вторая прямая проходит через точки (0; 5) и (85; 90). Нарисованные прямые делят квадрат на три части. Подставив координаты точки из средней части квадрата, например, точки (45; 45), убеждаемся, что оба неравенства выполняются в средней части квадрата, заштрихованной на рисунке.
Искомая вероятность будет равна отношению заштрихованной площади 
к площади квадрата. Величину можно найти, вычтя из площади квадрата площадь двух прямоугольных треугольников.
.
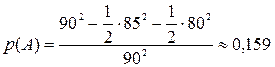Ответ: 0,159.
Задача 2
Определить надёжность схемы, представленной на рисунке, где - вероятность безотказной работы i -того элемента.
Решение
Соединение элементов, представленное на схеме, является комбинированным, так как содержит и последовательное и параллельное соединение.
Напомним, что при последовательном соединении система работает, если работают все элементы, соединённые последовательно; и не работает, когда не работает хотя бы один элемент. При параллельном соединении система работает, если работает хотя бы один элемент системы; и не работает, когда не работает ни один элемент.
Выделим участок схемы, содержащий последовательное соединение элементов (1) и (4) в отдельный элемент (5). Участок схемы, содержащий параллельное соединение элементов (2) и (3), выделим в элемент (6).
Обозначим В – событие, состоящее в том, что элемент (5) работает, 
- противоположное событие, состоящее в том, что элемент (5) не работает. Соответственное, событие С – это безотказная работа элемента (6), 
- событие состоящее в том, что элемент (6) не работает.
Событие, состоящее в том, что работает вся схема обозначим А. Так как элементы (5) и (6) соединены последовательно, то для наступления события А необходимо, чтобы работал хотя бы один из элементов (5) и (6): работают оба, работает (5) и не работает (6), не работает (5) и работает (6). Тогда событие А:
.
Соответственно, его вероятность
.
Учитывая, что
; 
;
; 
получим:
.
Ответ: вероятность безотказной работы схемы равна 0,963.
Задача 3
На склад поступают запасные детали от двух поставщиков. 60 % деталей приходит от первого поставщика, остальные 40 % - от второго. Среди продукции первого поставщика в среднем 5 % продукции оказываются нестандартными. В продукции второго поставщика нестандартных деталей в среднем 3 %.
а) Найти полную вероятность того, что наугад взятая запасная деталь окажется нестандартной.
б) Если наугад взятая деталь оказалась нестандартной, какова вероятность, что она от второго поставщика?
Решение
а) Обозначим А – событие, состоящее в том, что наугад взятая деталь нестандартная. Оно может произойти вместе с одним из двух событий, образующих полную группу: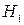 
- запасная деталь от первого поставщика; 
- деталь от второго поставщика. Тогда согласно формуле полной вероятности:
.
Используя данные задачи, вычислим:
.
б) Вероятность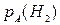 
того, что деталь от второго поставщика, если она оказалась нестандартной, найдём по формуле Байеса (формуле гипотез):
.
Ответ: а) 0,042; б) 0,286.
Задача 4
Вероятность поражения цели при одном выстреле равна 0,4. Произведено восемь выстрелов. Найти:
а) наивероятнейшее число попаданий и соответствующую ему вероятность;
б) вероятность того, что цель будет поражена не менее семи раз;
в) вероятность того, что цель будет поражена не более одного раза;
г) вероятность того, что цель будет поражена хотя бы один раз.
Решение
а) Наивероятнейшее число попаданий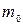 
найдём, используя двойное неравенство 
, учитывая, р = 0,4; п = 8:
.
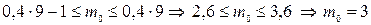Соответствующую этому числу попаданий вероятность найдём по формуле Бернулли:
.
б) Найдём вероятность того, что цель будет поражена не менее (т.е. равно и больше) семи раз. Для этого достаточно, чтобы она была поражена или семь, или восемь раз. Эти события несовместные, поэтому вероятность искомого события будет равна сумме вероятностей этих событий:
.
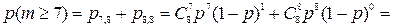
в) Найдём вероятность того, что цель будет поражена не более (т.е. равно или меньше) одного раза. Для этого достаточно, чтобы она была поражена или один раз, или ноль раз (ни одного разу). Так как эти события несовместные, искомая вероятность будет равна сумме вероятностей указанных событий:
г) Событием противоположным событию, состоящему в том, что цель поражена хотя бы один раз, будет событие, состоящее в том, что цель не поражена ни разу. Тогда нужную вероятность найдём по формуле:
.
Ответ: а) 3, 0,279; б) 0,0085; в) 0,1064; г) 0,9832.
