Моделирование дискретной случайной величины.
Случайная величина ξ называется дискретной, если она может принимать дискретное множество значений 
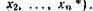
Дискретная случайная величина 
определяется таблицей
(Т)
где 
— возможные значения величины 
а
— соответствующие им вероятности. Точнее говоря, вероятность того, что случайная величина 
примет значение 
(обозначим через 
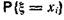), равна 
.
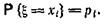
Таблица (Т) называется распределением случайной величины.
Числа 
могут быть, вообще говоря, любыми. Однако вероятности 
должны удовлетворять двум условиям:
а) все положительны:
(1)
б) сумма всех 
равна 1:
(2)
Последнее условие означает, что 
обязана в каждом случае принять одно из значений 
Математическим ожиданием случайной величины называется число
(3)
Отсюда видно, что 
— это среднее значение величины 
, причем более вероятные значения 
входят в сумму с большими весами. Отметим основные свойства математического ожидания: если с — какая-нибудь не случайная величина, то
(5)
если 
и 
— две любые случайные величины, то
(6)
Дисперсией случайной величины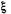 
называется число
(7)
Следовательно, дисперсия 
—это математическое
ожидание квадрата отклонения случайной величины 
от ее среднего значения 
. Очевидно, всегда 
Математическое ожидание и дисперсия — важнейшие числовые характеристики случайной величины 
.
Если мы будем наблюдать величину 
много раз и получим значения 
, 
,..., 
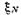(каждое из которых будет равно одному из чисел, 
, 
,..., 
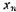), то среднее арифметическое от этих значений будет близко к 
:
(8)
А дисперсия 
характеризует разброс этих значений
около среднего 
Формулу для дисперсии можно преобразовать:
Откуда. 
. (9)
Для независимых случайных величин
(10)
Статистическую оценку для дисперсии можно получить по формуле
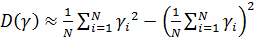(11)
Задание I
1.1.1 Согласно варианту выбрать таблицы распределения
.
1.1.2 Вычислить математическое ожидание и дисперсию случайных величин 
и 
по формулам (3) и (9) соответственно.
1.1.3 Построить таблицу распределения для случайной величины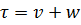 
.
1.1.4 Вычислить математическое ожидание и дисперсию случайной величины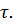 
1.1.5 Проверить соотношения (6) и (10).
1.1.6 Оформить отчёт в электронном виде.
Задание II
2.1 Построить алгоритмы, моделирующие дискретные случайные величины и величину по заданным таблицам распределения Задания I в виде отдельных функций.
2.2 Вычислить математическое ожидание по формуле (8)и дисперсию этих случайных величин по формуле (11)
2.3 Построить гистограмму распределений случайных величин, используя функцию histplot
2.4 Оформить отчёт в электронном виде.
2.5
Студент изучает теоретический материал и выполняет
Отчёт
Работа должна быть оформлена в виде электронного отчёта. Результаты должны включать теоретически материал, программы расчёты, «скриншоты» результатов работы программ, графики полученных распределений в виде гистограмм.
Студент должен знать:
1. определение дискретных случайных величин;
2. методы построения заданных распределений;
3. свойства и определения математического ожидания и дисперсии.
Варианты к заданию I и II
i = 1.
A =
93. 22. 48. 24. 8.
0.2295 0.3129 0.0637 0.2134 0.1803
B =
89. 45. 9. 75.
0.3662 0.2063 0.1571 0.2702
i = 2.
A =
28. 66. 46. 34. 55.
0.1963 0.245 0.1789 0.2136 0.166
B =
41. 38. 47. 12.
0.0559 0.3298 0.2989 0.3152
i = 3.
A =
43. 49. 99. 68. 63.
0.4971 0.1884 0.0119 0.0024 0.2999
B =
22. 44. 64. 19.
0.2784 0.3659 0.0962 0.2594
i = 4.
A =
42. 82. 83. 1. 25.
0.1967 0.2735 0.2169 0.2342 0.0785
B =
75. 64. 64. 55.
0.2611 0.4179 0.1383 0.1825
i = 5.
A =
3. 56. 44. 49. 56.
0.1334 0.0028 0.0451 0.1479 0.6705
B =
7. 22. 71. 61.
0.195 0.2701 0.2526 0.282
i = 6.
A =
87. 20. 70. 52. 52.
0.3044 0.1149 0.0752 0.3417 0.1636
B =
39. 67. 71. 48.
0.3519 0.1159 0.1597 0.3724
i = 7.
A =
31. 74. 12. 48. 9.
0.1201 0.334 0.1318 0.1787 0.2352
B =
50. 1. 29. 94.
0.0289 0.3238 0.3453 0.3018
i = 8.
A =
97. 10. 83. 5. 94.
0.2523 0.1969 0.2518 0.0452 0.2535
B =
12. 71. 76. 63.
0.281 0.2364 0.3786 0.1038
i = 9.
A =
76. 12. 21. 80. 93.
0.1674 0.2902 0.0382 0.451 0.053
B =
6. 31. 18. 42.
0.2386 0.2263 0.2174 0.3175
i = 10.
A =
0. 8. 31. 97. 90.
0.3055 0.4603 0.1364 0.0257 0.0719
B =
40. 70. 70. 58.
0.1933 0.075 0.5123 0.2192
i =
11.
A =
10. 48. 85. 48. 46.
0.0582 0.0048 0.0378 0.4622 0.4368
B =
27. 99. 80. 4.
0.2773 0.1447 0.4398 0.1379
i = 12.
A =
53. 55. 3. 94. 31.
0.2451 0.0196 0.2134 0.2428 0.2788
B =
75. 80. 37. 23.
0.323 0.4767 0.093 0.107
i = 13.
A =
87. 20. 66. 1. 93.
0.0114 0.4148 0.392 0.1062 0.0753
B =
33. 60. 25. 75.
0.4623 0.3832 0.1175 0.0368
i = 14.
A =
40. 19. 66. 33. 7.
0.2093 0.2853 0.0476 0.2938 0.1638
B =
72. 59. 67. 21.
0.3561 0.1849 0.0488 0.41
i = 15.
A =
25. 4. 95. 5. 51.
0.198 0.0518 0.2631 0.2444 0.2425
B =
92. 4. 70. 5.
0.1618 0.0117 0.4266 0.3997
i = 16.
A =
80. 43. 1. 95. 96.
0.1044 0.2071 0.2733 0.1911 0.2238
B =
53. 85. 69. 83.
0.2719 0.016 0.1982 0.5137
i = 17.
A =
34. 76. 59. 85. 49.
0.184 0.2691 0.1639 0.1633 0.2195
B =
92. 51. 63. 65.
0.3048 0.3914 0.1868 0.1168
i = 18.
A =
58. 94. 55. 31. 80.
0.0139 0.2804 0.1663 0.2897 0.2495
B =
50. 70. 0. 59.
0.0511 0.4585 0.4276 0.0625
i = 19.
A =
80. 20. 78. 42. 64.
0.2182 0.3343 0.2956 0.1465 0.0052
B =
89. 18. 11. 68.
0.1192 0.2051 0.3819 0.2935
i = 20.
A =
46. 48. 9. 32. 81.
0.209 0.2085 0.1998 0.2537 0.1286
B =
42. 4. 15. 95.
0.447 0.278 0.0345 0.2403
i = 21.
A =
16. 90. 64. 17. 81.
0.0206 0.3188 0.2552 0.3153 0.0898
B =
24. 24. 59. 10.
0.2956 0.2562 0.1937 0.2543
i = 22.
A =
8. 87. 17. 66. 93.
0.149 0.0783 0.057 0.408 0.3075
B =
78. 97. 49. 39.
0.3509 0.0727 0.347 0.2293
i = 23.
A =
77. 88. 91. 99. 80.
0.1386 0.0787 0.3747 0.0533 0.3544
B =
72. 82. 48. 98.
0.386 0.0609 0.0107 0.5422
i = 24.
A =
62. 42. 43. 90. 92.
0.2686 0.2869 0.2082 0.116 0.1201
B =
22. 27. 39. 30.
0.3343 0.4365 0.2168 0.0123
