Введение
Учебная дисциплина «Элементы высшей математики» является естественнонаучной дисциплиной, обеспечивающей общеобразовательный уровень подготовки специалиста.
Математика играет важную роль в естественнонаучных, инженерно-технических и гуманитарных исследованиях. Она стала для многих отраслей знаний не только орудием количественного расчета, но также методом точного исследования и средством предельно четкой формулировки понятий и проблем. Без современной математики с ее развитым логическим и вычислительным аппаратом был бы невозможен прогресс в различных областях человеческой деятельности.
Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки специалиста-программиста.
Учебным планом для студентов заочного отделения специальности 230115 «Программирование в компьютерных системах» предусмотрено выполнение домашней контрольной работы и проведение экзамена.
Разделы и темы курса «Элементы высшей математики», включенные в домашнюю контрольную работу для студентов заочного отделения специальности 23015 «Программирование в компьютерных система»:
- элементы линейной алгебры;
- элементы векторной алгебры и аналитической геометрии;
- теория пределов, непрерывность;
- дифференциальное исчисление функций одной действительной переменной
- интегральное исчисление функций одной действительной переменной;
- дифференциальное исчисление функций нескольких действительных переменных;
- обыкновенные дифференциальные уравнения;
- основы теории комплексных чисел.
Главное условие успешного овладения студентами основами высшей математики заключается в систематической самостоятельной работе.
Методические указания к выполнению контрольных работ
Цель контрольной работы – закрепление и проверка знаний, полученных студентами заочной формы обучения в процессе самостоятельного изучения учебного материала, а также выявления их умения применять на практике методы решения задач высшей математики.
Студент заочной формы обучения должен выполнить контрольную работу в установленные графиком учебного процесса сроки.
Если работа не будет зачтена, необходимо ознакомиться с внесенными в нее поправками и замечаниями, проанализировать ошибки и выполнить ее повторно, устранив недостатки, отмеченные преподавателем в рецензии.
Контрольная работа состоит из 10 задач. Распределение задач по темам курса приведено в таблице 1.
Таблица 1 - Распределение задач по темам курса
| № | № задачb | Тема |
| Линейная алгебра. Системы линейных уравнений. | ||
| Векторная алгебра. | ||
| Аналитическая геометрия. Прямая на плоскости. | ||
| Аналитическая геометрия. Кривые второго порядка. | ||
| Теория пределов. Пределы функций. | ||
| Дифференциальное исчисление функций одной действительной переменной. Вычисление производных. | ||
| Дифференциальное исчисление функций одной действительной переменной. Исследование функций. | ||
| Интегральное исчисление. Неопределенные интегралы. | ||
| Интегральное исчисление. Приложения определенного интеграла: вычисление площадей геометрических фигур. | ||
| Дифференциальные уравнения. Уравнения с разделяющимися переменными. | ||
| Комплексные числа. |
Требования к содержанию и оформлению контрольной работы
1. В заданиях приняты следующие обозначения
N – количество букв в полном имени студента;
 – количество букв в отчестве студента;
– количество букв в отчестве студента;
 – количество букв в фамилии студента.
– количество букв в фамилии студента.
2. Работа представляется либо в рукописном (текст выполняется разборчиво), либо в машинописном варианте. К текстам, подготовленным с помощью текстового процессора, предъявляются следующие требования: шрифт Times New Roman, 14 пт; междустрочный интервал 1,5; поля: верхнее – 2см, нижнее – 2 см., левое – 2,5 см, правое – 1,5 см.
3. В начале работы должен быть указаны значения параметров задания (N,  ). Работа, выполненная не по своему варианту, не учитывается и возвращается без оценки.
). Работа, выполненная не по своему варианту, не учитывается и возвращается без оценки.
4. Решение задач выполнять в порядке номеров, указанных в задании.
5. Каждая задача начинается с нового листа.
6. Перед решением задачи должно быть приведено ее условие.
7. Решение задач следует сопровождать необходимыми формулами, развернутыми расчетами и краткими пояснениями.
8. В конце работы должна стоять подпись студента с указанием даты ее выполнения.
9. На лицевой стороне контрольной работы необходимо указать следующую информацию: Ф.И.О. студента, номер группы, дисциплина и номер зачетной книжки.
Задача 1
Проверить совместность системы уравнений и в случае совместности решить ее:
а) по формулам Крамера;
б) с помощью обратной матрицы (матричным методом);
в) методом Гаусса.

Задача 2
По координатам А (5; N), В (–2;  ), С (–3;
), С (–3;  ) найти:
) найти:
а) модуль вектора  ;
;
б) угол между векторами  и
и  ;
;
в) площадь треугольника АВС;
г) координаты точки M, делящей отрезок AB в отношении 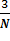 ;
;
д) уравнение прямой, на которой лежит сторона ВС.
Задача 3
Составить уравнение эллипса, симметричного относительно осей координат, с фокусами на оси ОХ, если расстояние между фокусами равно 2 Ф, а эксцентриситет равен  .
.
Задача 4
Вычислить пределы, не пользуясь правилом Лопиталя

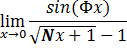


Задача 5
Найти производные третьего порядка указанных функций

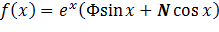
Задача 6
Исследовать методами дифференциального исчисления функцию и построить ее график.

Задача 7
Найти неопределенные интегралы. Результат проверить дифференцированием.


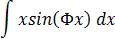
Задача 8
Вычислить площадь фигуры, ограниченной графиками функций
 и
и 
Задача 9
Найти общее решение дифференциального уравнения.
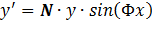
Задача 10
1) Записать число  в алгебраической форме;
в алгебраической форме;
2) изобразить его на координатной плоскости;
3) записать число a в тригонометрической и показательной форме;
4) вычислить  .
.
Вопросы для подготовки к экзамену
по дисциплине «Элементы высшей математики»
1. Матрицы. Операции над матрицами. Элементарные преобразования матриц. Ранг матрицы, его свойства.
2. Определители матриц. Свойства определителей.
3. Обратная матрица. Свойства обратной матрицы.
4. Системы линейных уравнений. Теорема Кронекера-Капелли. Правило решения произвольной системы линейных уравнений.
5. Решение систем линейных уравнений. Правило Крамера. Матричный метод.
6. Решение систем линейных уравнений. Метод Гаусса.
7. Векторы. Линейные операции над векторами.
8. Линейная зависимость векторов. Необходимые и достаточные условия коллинеарности и компланарности.
9. Понятие базиса. Аффинная система координат. Декартова прямоугольная система координат.
10. Скалярное произведение векторов, его свойства. Приложения скалярного произведения векторов.
11. Векторное произведение векторов, его свойства. Приложения векторного произведения векторов.
12. Смешанное произведение векторов, его свойства. Приложения смешанного произведения векторов.
13. Приложения метода координат: расстояние между двумя точками; деление отрезка в данном отношении; площадь треугольника.
14. Прямая на плоскости. Уравнение прямой с угловым коэффициентом.. Общее уравнение прямой. Уравнение прямой, проходящей через данную точку в данном направлении.
15. Прямая на плоскости. Уравнение прямой, проходящей через две точки. Уравнение прямой в отрезках. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
16. Прямая на плоскости. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Расстояние от точки до прямой.
17. Эллипс. Каноническое уравнение (вывод). Фокусы, фокальные радиусы, центр, вершины, полуоси, эксцентриситет, директрисы.
18. Гипербола. Каноническое уравнение (вывод). Фокусы, фокальные радиусы, центр, вершины, полуоси, асимптоты, эксцентриситет, директрисы.
19. Парабола. Каноническое уравнение (вывод). Фокус, директриса, параметр, вершина, эксцентриситет.
20. Множество действительных чисел, его свойства. Числовые промежутки. Окрестность точки. Ограниченные множества действительных чисел. Инфимум и супремум.
21. Числовая последовательность. Арифметические операции над числовыми последовательностями. Ограниченные последовательности. Верхние и нижние грани числовой последовательности.
22. Понятие функции. Область определения, множество значений. Способы задания функций. Монотонные функции. Сложная функция. Обратная функция.
23. 2Предел функции в точке.. Односторонние пределы. Пределы на бесконечности. Арифметические операции над функциями, имеющими предел. Бесконечно малые и бесконечно большие функции.
24. Определение непрерывности функции в точке и на множестве. Арифметические действия над непрерывными функциями. Непрерывность сложной функции.
25. Классификация точек разрыва функции.
26. Первый и второй замечательные пределы.
27. Определение производной. Геометрический смысл производной. Дифференцируемость функции. Производные высших порядков. Правила вычисления производных, связанные с арифметическими действиями над функциями. Правило дифференцирования сложной функции.
28. Дифференциал функции. Геометрический смысл дифференциала. Приложения дифференциала к приближенным вычислениям.
29. Правило Лопиталя.
30. Возрастание (убывание) функций. Локальный экстремум. Необходимое условие экстремума. Достаточное условие монотонности функции. Достаточные условия экстремума функции.
31. Выпуклость и вогнутость функции. Точки перегиба. Достаточные условия перегиба. Асимптоты графика функции.
32. Первообразная функция. Неопределенный интеграл. Основные свойства.
33. Неопределенный интеграл. Метод подведения под знак дифференциала. Метод подстановки.Интегрирование по частям.
34. Неопределенный интеграл. Метод неопределенных коэффициентов.
35. Понятие определенного интеграла, его геометрический смысл. Достаточное условие интегрируемости функции. Основные свойства определенного интеграла. Формула Ньютона-Лейбница.
36. Замена переменной и формула интегрирования по частям в определенном интеграле.
37. Геометрические приложения определенного интеграла: вычисление площадей плоских фигур, вычисление объемов тел вращения.
38. Дифференциальные уравнения первого порядка. Теорема существования и единственности решения задачи Коши. Дифференциальные уравнения с разделяющимися переменными.
39. Определение комплексного числа. Алгебраическая, тригонометрическая и показательная форма комплексного числа.
40. Операции над комплексными числами. Формула Муавра. Извлечение корней из комплексных чисел.
Список рекомендуемой литературы
Основная
1. Письменный, Д.Т. Конспект лекций по высшей математике: [в 2 ч.]. Ч. 2 / Дмитрий Письменный – М.: Айрис-пресс, 2008. – 256 с.
2. Письменный, Д.Т. Конспект лекций по высшей математике: [в 2 ч.]. Ч. 1 / Дмитрий Письменный – М.: Айрис-пресс, 2008. – 288 с.
3. Сборник задач по высшей математике. 1 курс. [К.Н. Лунгу и др.]; под ред. С.Н. Федина. – М.: Айрис-пресс, 2007. – 576 с.
4. Сборник задач по высшей математике. 2 курс / [К.Н. Лунгу и др.]; под ред. С.Н. Федина. – М.: Айрис-пресс, 2006. – 592 с.
Дополнительная
1. Баврин, И.И. Высшая математика: Учеб. для студ. естественнонаучных специальностей педагогических вузов / И.И. Баврин. – М.: Издательский центр «Академия»; высшая школа, 2000 – 616 с.
2. Малахов, А.Н. Высшая математика: Учебное пособие / А.Н Малахов, Н.И. Максюков, В.А. Никишкин. - М.: МЭСИ, 2002. - 352 с.
3. Никишкин, В.А. Практикум по дисциплине «Высшая математика» / В.А. Никишкин, Н.И. Максюков. А.Н. Малахов. – М.: МЭСИ, 2001. – 16 с.
4. Демидович, Б.П. Сборник задач и упражнений по математическому анализу: Учебное пособие для вузов / Б.П. Демидович. – М.: Наука, 1990. – 624 с.






