Метод минимальной кривизны

Этот метод эффективно заменяет участок реальной кривой ствола между двумя точками замера сферической дугой. Т.е. требуется найти пространственный вектор, который определяется углами наклона и направления в каждой из двух точек замера и который плавно соединял бы дугу с этими точками при помощи фактора отношения, определяемого кривизной участка ствола (см.рис. 4-7).

Этот метод - один из наиболее точных в определении положения ствола сква­жины.

 

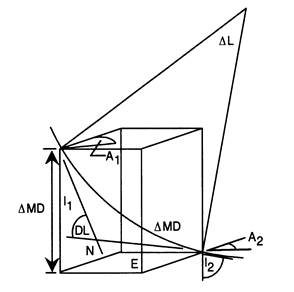Рисунок 4-7

Кривизна (Dog-leg) DL = cos-1[cos(I2-I1) - sinI1sinI2(1 - cos(A2-A1)]   Фактор отношения (RF) Курсовая длина MD измеряется вдоль кривой, в то время как I и А определяют направ­ления прямых линий в пространстве. Необходимо совместить эти прямые с сегментами кривой при помощи фактора отношения, определяемого как: RF = 360 tan (DL/2) [ DL/p ]-1

 

или

RF = 360*(1 - cosDL) *[ DL*p *sinDL ]^-1

Где DL выражается в градусах. Для маленьких углов (DL <.0001), RF полагают равным 1. Затем мы можем определить увеличение по трем осям для определения следующей точки замера

DTVD = (DMD/2) (cosI₁+cosI₂) RF

DNorth = (DMD/2) (sinI₁cosA₁+sinI₂cosA₂) RF

DEast = (DMD/2) (sinI₁sinA₂+SinI₂sinA₂) RF

На сегодняшний день метод минимальной кривизны - наиболее точный. Именно его Анадрилл выбрал в качестве расчетного.

 

Метод Меркюри

Свое название он получил по месту первого применения в Меркюри, Невада, при бурении шахты для испытания атомной бомбы. В нем скомбинированы тангенци­альный и сбалансированный тангенциальный методы и учитывается длина измеритель­ного прибора. (STL). В нем, та часть измеряемой кривой, где находится измерительный прибор, рассматривается как отрезок прямой линии, а остальная часть кривой рассчи­тывается сбалансированным тангенциальным методом

DTVD = [ (DMD - STL)/2 ] *(cosI₁+cosI₂) + STL*cosI₂

DNorth = [(DMD-STL)/2](sinI₁cosA₁+sinI₂cosA₂) + STL sinI₂cosA₂

DEast = [(DMD-STL)/2](sinI₁sinA₁ + sinI₂sinA₂) + STL sinI₂sinA₂

Относительная точность различных методов

Предположим, что существует скважина, пробуренная в направлении на север длиной 2000’ MD cо скоростью набора угла 3/100’ и расстояниями между замерами параметров в 100’. Можно вычислить относительную точность различных методов. Сравнивая с “действительной” TVD, равной 1653,99’ и отходом на север в 954,93’ мы находим следующее.

Ясно, что это лишь показатель относительной точности и наиболее предпочти­тельным оказывается тот метод, который представляет ствол скважины в виде серии сегментов длин окружностей. Действительный профиль скважины может не совпадать с вычисленным.

Необходимо отметить, что в приведенном примере не рассматривалось измене­ние азимутального угла, хотя его следовало бы учесть при оценке точности расчетов. Однако, совершенно очевидно, что учет и этого параметра только лишь еще больше увеличит расхождения в вычислениях трехразмерного случая.

 

Интенсивность

Интенсивность является мерой изменения величины наклона и/или направления ствола скважины. Обычно она выражается в градусах на 100 футов или в градусах на 10 или 30 метров.

Для вычисления суммарного эффекта как изменения направления, так и наклона между точками замера применимы несколько формул:

d = DLS интервал

I₁ = Наклон в 1 точке замера

A₁ = Азимут в 1 точке

I₂ = Наклон во 2 точке

A₂ = Азимут во 2 точке

формула, применимая во всех случаях:

1. DLS = (d/DMD)2sin^-1{[(sinDI/2)² + (sinDA/2)² * sinI₁sinI₂]}^1/2

для тангенциального метода.

2. DLS = (d/DMD)cos^-1 [(sinI₁sinI₂)(sinA₁sinA₂+cosA₁cosA₂)+(cosI₁cosI₂)]

для модели минимальной кривизны.

3. DLS = (d/DMD)cos^-1[cosDI - (sinI₁sinI₂)(1 - cosDA)]

Все три уравнения идентичны тригонометрически и можно пользоваться любым из них. Необходимо только иметь в виду, что вычисление косинусов при малых углах значительно труднее, чем синусов если нет специальных вычислительных средств.

Таблица 4-1

Метод вычисления	Ошибка по TVD (ft)	Ошибка в отходе (ft)
Тангенциальный Сбалансированный танген­циальный	-25,38   -0,38	+43,09   -0,21
Метод среднего угла	+0,19	+0,11
Радиус кривизны	0,00	0,00
Минимальной кривизны	0,00	0,00
Меркюри (STL=15’)	-0,37	-0,04