Поскольку все реакции опорных связей уже определены (см. п. 2), приступаем к построению многоугольника внешних сил. Эта процедура основана на понятии «внешнего поля».
Внешние поля (рис. 14) делят плоскость чертежа вне расчетной схемы на части, границами между которыми являются векторы внешних сил. Каждое поле получает свое имя в виде буквы, благодаря чему при пересечении границы полей возникает возможность именования соответствующих векторов сил двумя буквами: одна буква соответствует началу вектора, а вторая – его концу.
Рис. 14
Начало вектора силы определяется той буквой, поле которой названо первым при пересечении границы смежных полей в выбранном направлении обхода.
Многоугольник внешних сил в данном примере строится путем обхода внешних полей против часовой стрелки, начиная с поля «А», как это показано на
рис. 14. По мере пересечения границ внешних полей соответствующая внешняя сила в назначенном масштабе наносится на поле диаграммы усилий (рис. 15).
Поскольку равновесие расчетной схемы соответствует нулевым значениям главного вектора и главного момента внешних сил, постольку многоугольник внешних сил должен получиться замкнутым. Если это реализуется в ходе построения, то можно утверждать, что реакции в расчетной схеме найдены верно.
|
|
Рис. 15
Дальнейшие построения связаны с определением внутренних сил (усилий) в стержнях фермы. В основе этой процедуры лежит построенный многоугольник внешних сил (см. рис. 15), а приведенные выше приемы рассуждений применяются к полям, окружающим каждый узел.
Важно помнить, что выбор узла при построении многоугольника сил, в нем сходящихся, определяется тем, что в узле может сходиться не более двух неизвестных усилий. При этом направление обхода полей узла должно соответствовать направлению обхода, использованному при построении многоугольника внешних сил, т. е. против часовой стрелки.
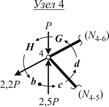
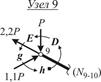
На рис. 16-24 последовательно отображены результаты построения многоугольников сил в узлах заданной расчетной схемы. Для пояснения совершаемых действий используются следующие обозначения:
«
» – означает, что проводится линия по направлению, параллельному пересекаемому стержню фермы, обозначенному парой букв;
«через...» – точка вектора, через которую проводится параллельная прямая, упоминаемая выше;
«■» – поле, с которого начинается обход полей, расположенных вокруг узла;
«
» – вектор силы, участвующей в создании многоугольника равновесных сил, сходящихся в текущем узле.
Рис. 16
| 
|
Рис. 17
| 
|
Рис. 18
| 
|
Рис. 19
| 
|
Рис. 20
| 
|
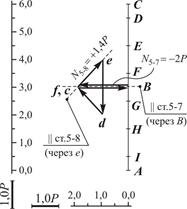Рис. 21
| 
|
Рис. 22
| 
|
Рис. 23
| 
|
Рис. 24
| 
|
В данном примере реализуется последовательность узлов, основанная на результатах текущих построений (каждый последующий узел превращается в узел с двумя неизвестными усилиями вследствие решения задачи о равновесии предыдущего узла) и включает узлы 1, 2, 3, 4.
Однако узел 5 уже не может рассматриваться вслед за узлом 4, поскольку к этому моменту содержит три неизвестных усилия (
, 
и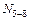 
). Поэтому далее выбирается узел 6 с двумя неизвестными усилиям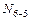и (
и 
), а за ним становится возможным перейти к узлу 5 с неизвестными к этому моменту усилиями и 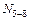. Далее аналогично рассматриваются узлы 8, 7 и, наконец, построения в узле 9 с единственным неизвестным усилием 
завершают решение задачи.
Определение величины усилия проводится измерением длины построенного вектора, а знак усилия определяется тем, как вектор направлен по отношению к рассматриваемому узлу: если направление «от узла», то в соответствии с «инженерным» правилом знаков это означает «положительность» искомого усилия; если же направление «к узлу» – «отрицательность» усилия.
Решение задачи в окончательном виде представлено на рис. 25 и табл. 4. Следует подчеркнуть, что данные табл. 4 получены измерением усилий на рис. 16-24(рис. 25) с использованием выбранного масштаба построений.Рис. 25 носит название «диаграммы Максвелла-Кремоны» или «диаграммы усилий».
|
Таблица 4
| Номер стержня | 1–2 | 1–3 | 2–3 | 2–4 | 3–4 | 3–5 | 4–5 | 4–6 | 6–5 |
| 9–10 | 7–10 | 7–9 | 8–9 | 7–8 | 5–7 | 5–8 | 6–8 | ||
| Знак усилия | + | – | – | + | – | – | + | + | – |
Усилие  , P
| 1,1 | 1,1 | 2,2 | 2,5 | 1,4 | 1,1 |
При соблюдении правил построения диаграмма усилий позволяет быстро и достаточно точно решить задачу об определении усилий в статически определимой расчетной схеме типа «ферма». Поэтому графический способ определения усилий рекомендуется всегда, когда допустимая погрешность определения усилий находится в пределах 10 %.
Так как продольные усилия в стержнях заданной фермы, вычисленные аналитическим и графическим способами (соответственно табл. 3 и табл. 4) имеют схожие значения, то можно утверждать, что оба расчета были сделаны верно.
Подставляя заданное в кН значение нагрузки P, окончательно будем иметь:
ü 
кН;
ü 
кН;
ü 
кН;
ü 
кН;
ü 
кН;
ü 
кН;
ü 
кН;
ü 
кН;
ü 
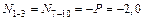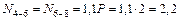кН.
ЛИТЕРАТУРА
1. Яблонский А.А., Никифорова В.М. Курс теоретической механики, ч. I, – М., 1971 и последующие издания.
2. Сборник заданий для курсовых работ по теоретической механике / Под ред. Яблонского А.А. – М.: Интеграл-Пресс, 2003. – 384 с.
3. Теличко Г.Н. Основы строительной механики плоских стержневых систем: Учебник. – Тула: ТулГУ, 1999. – 440 с.
