Лабораторная работа № 1
Определение фокусного расстояния
Собирающей и рассеивающей линз
Цель работы: приобретение практических навыков по экспериментальному определению фокусного расстояния собирающей и рассеивающей линз.
Теоретические основы эксперимента
Линзой называется тело с определённым показателем преломления n, ограниченное двумя сферическими поверхностями. Тонкой линзой называется линза, у которой расстояние между ограничивающими поверхностями мало по сравнению с диаметром линзы. Линзы бывают двух видов: собирающая и рассеивающая линзы.
Типы собирающих линз (рис.1):
1) двояковыпуклые линзы,
2) плоско - выпуклые линзы,
3) выпукло - вогнутые линзы.
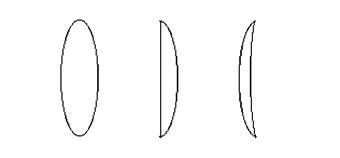
1 2 3
Рис.1
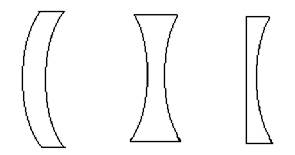
Типы рассеивающих линз (рис.2):
1)вогнуто – выпуклые линзы,
2) двояковогнутые линзы,
3) плоско – вогнутые линзы.
1 2 3
Рис. 2
Линия, проходящая через центры кривизны обеих поверхностей, называется главной оптической осью линзы.
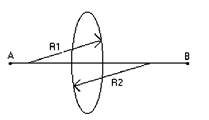
Рис.3.
На рис.3 АВ - главная оптическая ось, R1, R2 - радиусы кривизны линзы.
Точка F (рис.4) на главной оптической оси, в которой пересекаются после преломления лучи, параллельные этой оси, называется главным фокусом. У собирающей линзы фокусы действительные, у рассеивающей - мнимые. ОF -фокусное расстояние линзы.
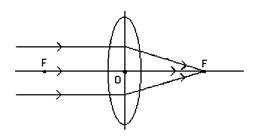
Рис.4.
Соответственно для рассеивающей линзы:
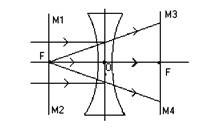
Рис.5
Плоскость, которая перпендикулярна главной оптической оси линзы, а также проходит через её главный фокус, называется фокальной. М1М2, М3М4 -фокальные плоскости. Побочный фокус F1 - это точка на фокальной плоскости М3М4, в которой собираются лучи падающие на линзу параллельно побочной оси (рис.6).
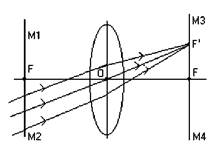
Рис.6.
Часто возникает необходимость знания фокусных расстояний линз, используемых в сложных оптических системах. Элементарная теория тонких линз приводит к простым соотношениям между фокусным расстоянием тонкой линзы с одной стороны и расстоянием от линзы до предмета и изображения, с другой стороны. Простой оказывается также связь между размерами объекта и его изображением, даваемого линзой, и их расстоянием до линзы. Методами геометрической оптики найдём связь между фокусным расстоянием линзы, расстоянием от предмета до линзы и расстоянием от линзы до изображения предмета.
На рис.7 изображена тонкая двояковыпуклая линза, у которой радиусы кривизны R1, R2 поверхностей положительны. Расчёт будем вести в общем виде, пригодном для линз любой формы (выпукло - вогнутая, плоско - вогнутая).
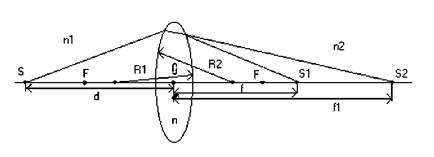
Рис.7.
Так как линза тонкая, то отсчёт расстояний до предмета d и до изображения f можно вести практически от одной точки О - оптического центра линзы. Показатели преломления сред, расположенных перед и после линзы, обозначим соответственно через n1 и n2.
Лучи, исходящие от источника света S, лежащего на главной оптической оси, преломившись на передней поверхности линзы, пересекутся в некоторой точке S 2, расположенной на расстоянии f 1от оптического центра. Запишем для такой системы инвариант Аббе:
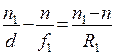(1)
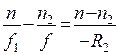(2)
Вычитая почленно равенства (1) и (2) и исключая тем самым величину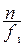 
,
характеризующую положение промежуточного изображения S2, получаем окончательно
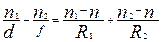(3)
Это уравнение позволяет найти расстояние до изображения f, если известно расстояние до предмета d, радиусы кривизны обеих поверхностей линзы R1 и R2 показатель преломления вещества линзы n и показатели преломления сред, расположенных до и после линзы n1 и n2.
Для линзы, расположенной в однородной среде (например, в воздухе), п 2 = n1 и соотношение (3) упрощается:
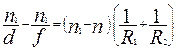(4)
Вводя относительный показатель преломления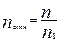 
, можно привести формулу линзы к окончательному виду
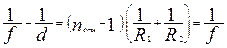(5)
Величина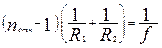 
(6)
называется оптической силой линзы, а обратная ей величина f - главным фокусным расстоянием.
Если измерять фокусное расстояние f в метрах, то оптическая сила линзы будет измеряться в диоптриях:
1диоптрия=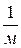 
.
Вводится ещё одна величина (характеризующая линзу) которая называется линейное увеличение:
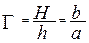, (7)
где h - высота предмета, Н - высота соответствующего изображения (рис.8).
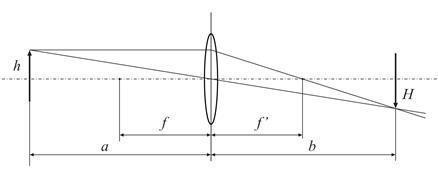
Рис.8.
Ниже описаны способы, позволяющие экспериментально определить величину фокусного расстояния собирающей линзы и способ, позволяющий определить фокусное расстояние рассеивающей линзы [1].
Способ 1, основанный на определении расстояния от линзы до предмета и до его изображения.
Помещая предмет перед тонкой собирающей линзой, получают его действительное изображение на экране (рис.8).
Измеряя расстояние от линзы до предмета ОВ = a и до изображения ОВ 1= b, по формуле линзы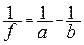 
вычисляют (с учетом правила расстановки знаков) ее фокусное расстояние F:
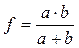(1)
При выводе этой формулы предполагалось, что толщина линзы достаточно мала по сравнению с a и b.
Способ 2, основанный на определении величины предмета и его изображения, и измерении расстояния последнего от линзы.
Обозначим величину предмета буквой h, величину изображения Н и расстояния от линзы соответственно a и b (рис. 8).
Эти величины связаны между собой соотношением
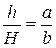; из этого следует 
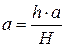(2)
Подставив (2) в формулу (1) легко получить следующую формулу для вычисления фокусного расстояния линзы:
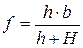(3)
Способ 3 (Бесселя). Определение фокусного расстояния по величине перемещения линзы.
Это один из самых точных методов измерения фокусного расстояния линзы. Если расстояние от предмета до изображения более 4f, то всегда найдутся два таких положения линзы, при которых на экране получится отчетливое изображение предмета. На рис.9 показаны положение 1 линзы, при котором получается увеличенное изображение С/В/ и положение 2 линзы, при котором получается уменьшенное изображение С//В//. Здесь А - расстояние от предмета до изображения, l - величина перемещения линзы из 1 в 2.
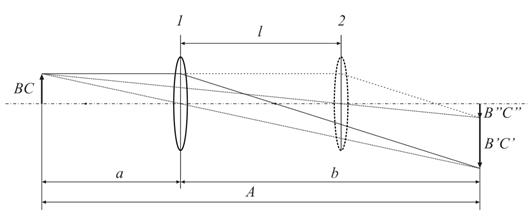
Рис.9 Измерение фокусного расстояние методом Бесселя.
Можно заметить, что при обеих положениях линза будет симметрична относительно середины расстояния между предметом и изображением. Действительно, воспользовавшись уравнением (1), можно записать для первого и второго положения линзы:
f = (А – l – х) (х + l)/А и f = (А – х) х / А
Приравнивая, правые части этих уравнений, найдем х. Подставляя значение х в выражение А-l-х, найдем что А-l-х = (А-l)/2. То есть действительно оба положения линзы находятся на равных расстояниях от предмета и изображения и, следовательно, симметричны относительно середины расстояния между ними.
Чтобы получить выражение для фокусного расстояния, рассмотрим одно из расположений линзы, например, когда расстояние от предмета до линзы a=А-l/2, а расстояние от линзы до изображения b=(А+l)/2. Подставив эти величины в формулу (1), найдем:
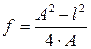(4)
Этот способ является принципиально более общим и пригодным как для толстых, так и для тонких линз. Действительно, когда в предыдущих случаях пользовались для расчетов величинами отрезков, измеренных от центра линзы, на самом же деле следовало эти величины измерять от соответствующих главных плоскостей линзы, определение которых довольно затруднительно. В описанном способе эта ошибка исключается, благодаря тому, что в нем используются не расстояния от линзы, а лишь величина перемещения.
