Теперь для интерполяции множеств можно использовать формулу (1). Она примет вид:
 . (2)
. (2)
Чтобы осуществить построение переходного множества при некотором значении t,нужно сначала построить множества  и
и  , далее найти их сумму.
, далее найти их сумму.
Пример 4. Пусть  – круг радиуса
– круг радиуса  с центром в точке
с центром в точке  =
=  (0;0),
(0;0),  – круг радиуса
– круг радиуса  с центром в некоторой точке
с центром в некоторой точке  . Тогда интерполяционное множество
. Тогда интерполяционное множество  (
( ) – это круг с центром в точке
) – это круг с центром в точке  , расположенной на отрезке
, расположенной на отрезке  /
/ 
 /, радиуса
/, радиуса  (рис.9).
(рис.9).

Рис.9. Интерполяция двух кругов
Действительно, зафиксировав некоторое значение t ( ), построим множества
), построим множества  и
и  . Окажемся в условиях примера 2. Переписав его результат в текущих обозначениях, получаем нужное утверждение. Видим, что в этом случае переходные изображения (круги) примыкают к общим касательным, проведённым к двум исходным кругам, т.е. результаты интерполяции очень хорошо согласуются с нашими наглядными представлениями о переходных изображениях.
. Окажемся в условиях примера 2. Переписав его результат в текущих обозначениях, получаем нужное утверждение. Видим, что в этом случае переходные изображения (круги) примыкают к общим касательным, проведённым к двум исходным кругам, т.е. результаты интерполяции очень хорошо согласуются с нашими наглядными представлениями о переходных изображениях.
Замечание. Из свойств арифметических операций над множествами следует, что аналогичная картина получится при интерполяции двух любых кругов. Действительно, круг  радиуса
радиуса  с центром в произвольной точке
с центром в произвольной точке  может быть представлен в виде суммы круга
может быть представлен в виде суммы круга  радиуса
радиуса  с центром в точке
с центром в точке  (0;0) и множества, состоящего из одной точки
(0;0) и множества, состоящего из одной точки  (равносильно вектора
(равносильно вектора  ):
):  =
=  +
+ 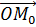 . Тогда интерполяционная формула даёт:
. Тогда интерполяционная формула даёт:
 =
= 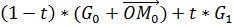 =
=  +
+ 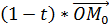 .
.
Остаётся заметить, что семейство векторов  ,
,  , является переходным от вектора
, является переходным от вектора 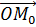 к нулевому вектору.
к нулевому вектору.
Таким образом, для удобства осуществления интерполяции (выполнения арифметических операций) можно всегда брать множества (фигуры), примыкающие к началу координат, поскольку произвольные заданные множества сводятся к такой ситуации сдвигом на определённые векторы. Эти векторы затем нужно тоже проинтерполировать (с тем же значением параметра t).
Среди важных особенностей метода отметим факт, что при интерполяции двух многоугольников, вершины интерполяционного многоугольника получаются интерполяцией (с тем же значением t) вершин исходных многоугольников. Это следует из того, что арифметические операции над множествами определяются через арифметические операции над отдельными их векторами. Получить «экстремальный» вектор в переходном множестве можно лишь, складывая соответствующие «экстремальные» векторы в исходных множествах.
Пример 5. Пусть  – квадрат 2 x 2 с правой нижней вершиной в начале координат,
– квадрат 2 x 2 с правой нижней вершиной в начале координат,  – прямоугольник 4 x 5 с левой нижней вершиной в начале координат (стороны обеих фигур параллельны осям координат) (рис. 10). Построим интерполяционное множество
– прямоугольник 4 x 5 с левой нижней вершиной в начале координат (стороны обеих фигур параллельны осям координат) (рис. 10). Построим интерполяционное множество  .
.
1 способ. Воспользуемся формулой (2) при  . Построив множества
. Построив множества
 и
и  (их границы на рисунке 10 проведены пунктирными линиями), находим их сумму. Получим прямоугольник
(их границы на рисунке 10 проведены пунктирными линиями), находим их сумму. Получим прямоугольник  .
.

Рис.10. Интерполяция прямоугольников на основе арифметических операций
2 способ. Сопоставим соответствующие вершины исходных прямоугольников (в данном случае их соответствие очевидно, на рис. 11 оно показано отрезками); проинтерполировав каждую из этих пар точек (векторов) с заданным  , получим вершины интерполяционного множества (прямоугольника).
, получим вершины интерполяционного множества (прямоугольника).

Рис.11. Интерполяция прямоугольников путём интерполяции вершин
Снова обсуждаемый метод интерполяции даёт такой результат, какой мы ожидали бы увидеть.
Пример 6. Пусть  – прямоугольные равнобедренные треугольники с гипотенузой h =100 и общей вершиной в начале координат. Тогда в результате интерполяции по Минковскому при
– прямоугольные равнобедренные треугольники с гипотенузой h =100 и общей вершиной в начале координат. Тогда в результате интерполяции по Минковскому при  получим шестиугольник (интерполяционное множество
получим шестиугольник (интерполяционное множество  ) (рис. 12).
) (рис. 12).

Рис.12. Интерполяция симметричных треугольников
Вычисления по интерполяционной формуле (2) сразу приводят к указанному итогу. В отличие от предыдущего примера, в случае данных треугольников сопоставление вершин, осуществляемое методом Минковского, как и сам результат, оказывается несколько неожиданным. Действительно, попарная интерполяция «верхних» и «нижних» вершин треугольников при даёт соответственно «верхнюю» и «нижнюю» вершины шестиугольника. А вот вершины прямых углов треугольников «интерполируются» с каждой из «верхней» и «нижней» вершин другого треугольника.
Результат примера 6, конечно, оставляет вопросы. Однако если вдуматься, то вряд ли мы сможем предложить «логичный» вариант переходного множества. Изначально предполагалось интерполировать «близкие», сходные изображения. См. также ниже замечание об особенностях интерполяции противоположных векторов.
Ещё более удивителен следующий случай.
Пример 7. Пусть  – отрезки на осях координат:
– отрезки на осях координат: 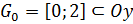 ,
,
 . Тогда
. Тогда  – квадрат со стороной единица, нижние вершины которого расположены в точках (1;0) и (2;0) (рис. 13).
– квадрат со стороной единица, нижние вершины которого расположены в точках (1;0) и (2;0) (рис. 13).

Рис.13. Интерполяция отрезков
Множества  и
и  представляют собой соответственно отрезки
представляют собой соответственно отрезки  и
и  . Складывая их /прибавляя к каждой точке (вектору) отрезка
. Складывая их /прибавляя к каждой точке (вектору) отрезка  отрезок
отрезок  (всевозможные векторы из него)/, получаем квадрат. В условиях примера 7 по наглядным представлениям переходным множеством, очевидно, должен бы быть отрезок, но особенности метода интерполяции приводят к прямоугольнику.
(всевозможные векторы из него)/, получаем квадрат. В условиях примера 7 по наглядным представлениям переходным множеством, очевидно, должен бы быть отрезок, но особенности метода интерполяции приводят к прямоугольнику.
Анализируя разобранные примеры, можно увидеть, что алгоритм Минковского даёт блестящие результаты в случаях, когда:
1)  ,
,
2)  получено из
получено из  параллельным переносом,
параллельным переносом,
3) Когда пункты 1 и 2 выполняются одновременно.
 В других случаях работа алгоритма может быть неудовлетворительной. В частности, когда множества
В других случаях работа алгоритма может быть неудовлетворительной. В частности, когда множества  и
и  получаются поворотом друг из друга. Корни такого положения вещей кроются в самом подходе: уже для векторов, между которыми значительный угол, результат интерполяции получается плохой (рис. 14).
получаются поворотом друг из друга. Корни такого положения вещей кроются в самом подходе: уже для векторов, между которыми значительный угол, результат интерполяции получается плохой (рис. 14).
Рис.14. Интерполяция векторов, образующих большой угол
Важным моментом в представленном методе является то, что на его «фундаменте» можно строить новые, более совершенные алгоритмы. Они имеют важный прикладной характер и активно используются в современной технике.
В заключение параграфа отметим, что изображения (множества точек) с введёнными на них операциями по Минковскому не образуют линейное пространство, поскольку не все соответствующие аксиомы сложения и умножения имеют место.
Пример 8. Пусть задано множество  , симметричное относительно начала координат. Тогда
, симметричное относительно начала координат. Тогда  = –
= – 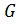 , но понятно, что это множество не обязано быть нейтральным элементом относительно сложения (нулём). Кроме того,
, но понятно, что это множество не обязано быть нейтральным элементом относительно сложения (нулём). Кроме того,
 –
–  =
=  +(–
+(–  ) =
) =  +
+  = 2
= 2 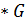 .
.
С этим связаны дополнительные ограничения на применение арифметических операций над множествами в алгоритмах.
Тем не менее, если использовать только положительные числа, всё выполняется. Такая структура в математике называется «конусом». Т.е. изображения с заданными на них операциями по Минковскому образуют «конус».




