ЛЕКЦИЯ №2
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Дискретная и непрерывная случайные величины.
Понятие случайной величины.
Наряду со случайными событиями одним из основных понятий теории вероятностей является понятие случайной величины.
Случайной величиной называется переменная, принимающая в результате испытания одно из возможного множества некоторое, наперед неизвестное значение, которое может изменяться от испытания к испытанию.
Случайные величины принято обозначать 
, их возможные значения - 
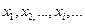
Случайные величины могут классифицироваться следующим образом:
· Величины количественные и качественные. Количественные величины называются также числовыми.
· Величины одномерные и многомерные.
· Величины дискретные и непрерывные (для числовых величин).
Дискретной случайной величиной называется случайная величина, принимающая отдельные, изолированные друг от друга значения. (ДСВ).
Возможные значения дискретной случайной величины образуют конечное или счетное множество.
Непрерывной (НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.
Примеры случайных величин:
1) число родившихся детей в течение суток в г.Москве;
2) количество бракованных изделий в данной партии;
3) число произведенных выстрелов до первого попадания;
4) число выпавших очков при бросании игральной кости;
5) дальность полета артиллерийского снаряда;
6) расход электроэнергии на предприятии за месяц.
Для задания случайной величины недостаточно знать только ее возможные значения. Две случайные величины могут иметь одинаковые значения, но принимать их с различными вероятностями (например, оценки на экзамене у сильных и слабых студентов). Поэтому необходимо указать и возможные значения, и их вероятности.
Закон распределения дискретной случайной величины.
Законом распределения дискретной случайной величины называется соответствие между возможными значениями это величины и их вероятностями.
Способы задания закона распределения:
1) Табличный способ – в первой строке таблице в порядке возрастания перечисляются возможные значения случайной величины, во второй – их вероятности.
| X | x1 
| x2 | … | xi | … | xn |
| P | p1 | p2 | … | pi | … | pn |
В данной таблице pi – вероятность того, что случайная величина X приняла значение xi (
), причем сумма вероятностей в нижней строке должна быть равна единице: 
. Такую таблицу называют рядом распределения вероятностей дискретной случайной величины.
2) Графический способ – по оси абсцисс откладываются возможные значения случайной величины, по оси ординат – их вероятности. Полученные точки соединяются отрезками. Такой график называют многоугольником (полигоном) распределения.
3) Аналитический способ – соответствие между значениями случайной величины и их вероятностями задается с помощью формулы:
