Лекция 2
Нормативные условия состояния ТС
Нормальные физические условия, которые характеризуются следующими параметрами состояния: абсолютноедавление Р = Р 0 = 760 мм рт. ст. = 1 атм = 101325 Па, температура Т = Т 0 = 273,15 К (t0 = 0 0С).
Стандартные физические условия, которые близки к условиям физических лабораторий и характеризуются следующими параметрами состояния: абсолютное давление Р = 1 атм, температура t = 20 0С.
Нормальные технические условия, которые характеризуются следующими параметрами состояния: абсолютноедавление Р = 1 ат = 98066,5 Па, температура t = 15 0С.
Стандартные термодинамические условия (условия стандартного состояния веществ). Это условия наиболее стабильного состояния веществ. Если нет специальногоуказания, то стандартные термодинамические условия характеризуются следующими параметрами: абсолютное давление Р = 1 атм, температура Т = 298,15 К (t = 25 0С).
В технической литературе для оценки объёмных характеристик газов при нормальных физических условиях иногда используется условное обозначение «нор. м3», которая читается как «нормальный метр кубический» и указывает на то, что рассматриваемый газ отнесён к нормальным физическим условиям, то есть к Р = Р0 и Т = Т0.
Молярный объём идеального газа - физическая константа: 
Уравнения состояния идеального газа
При использовании данных полученных в опытах с газами был сформулирован для идеальных газов объединённый газовый закон (объединённый закон Бойля-Мариотта и Гей-Люссака):
При 
он превращается в закон Бойля-Мариотта - 
При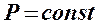 
- в закон Гей-Люсака - 
а при 
в закон Шарля - 
Взяв за основу
объединённый газовый закон Б.П.Э. Клапейрон в 1834 г. термическое уравнение состояние идеального газа (уравнение Клапейрона):
(2.2.5)
или 
, (2.2.6)
где [ R ] = [ Pv/T ] = Дж/(кг×К).
или 
. (2.2.7)
. (2.2.8)
Взяв за основу уравнение Клапейрона, Менделеев Д. И. получил универсальное уравнение состояния идеального газа (Уравненеи Клапеёрона-Менделеева):
Pvm = mRT (2.2.14)
Учитывая, что vm = Vm получаем:
PVm= mRT. (2.2.15)
PVm= RmT, (2.2.17)
где [ Rm ] = [ mR ] = Дж/(моль×К).
PVmnm = nm RmT, ® PV = nm RmT, 
. (2.2.18)
и 
. (2.2.26)
. (2.2.27)
Учитывая, что v = 1/ r из(2.2.27)получаем:
Составы многокомпонентных веществ (смесей)
Составы: массовый, объёмный, молярный.
Массовый состав измеряется в массовых долях.
Массовая доля mд,i i-го компонента в смеси – отношениемассы этого компонента Мi к массе всей смеси Мсм:
. (3.2.1)
Вполне очевидно, что:
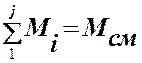, а 
, (3.2.2)
где j – количество компонентов в смеси; [ mд,i ] = дол. ед. (см. 3.2.1) или % по массе (мас. %).
Объёмный состав измеряется в объёмных долях.
Объёмная доля vд,i i-гокомпонента в смеси– отношение объёмаi-готвёрдого или жидкого компонента,а для смесейгазов и паров жидкостей отношениепарциального (приведённого) объёма VП,i этого газообразного компонента к объёму всей смеси Vсм.
Таким образом:
для жидких и твёрдых смесей:
для газообразных смесей:
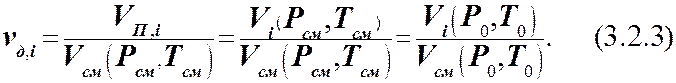
где 
.
Использование парциального объёмаVП,i (в ряде литературных источников он назван приведённым объёмом) при определении величин vд,i в смесях газов и паров жидкостей обусловлено тем, что каждый газовый компонент в этих смесях занимает объём равный объёму всей смеси, то есть Vсм. Это открыто около 2-х веков назад известным английским учёным Д. Дальтоном. Сформулированный им закон гласит: если смесь состоит из газов, которые не вступают между собой в химические реакции, то каждый газ ведёт себя так, как будто он один занимает весь объём сосуда, в котором находится газовая смесь и производит соответствующее давление на стенки этого сосуда. Подтверждение этого закона следует, например, из того факта, что человек может дышать кислородом воздуха в каждой точке комнаты, где он только может находиться. Следовательно, кислород занимает весь объём комнаты. Однако если при определении объёмной доли кислорода в воздухе комнаты будет учитываться этот объём, то получится, что содержание кислорода в воздухе должно равняться, согласно (3.2.3), 100 % по объёму. Но этого принципиально быть не может, так как воздух содержит ещё и другие газы, объём которых также равен объёму комнаты.
Чтобы устранить возникший парадокс, и было введено понятие парциального (приведённого) объёма газового компонента в смеси. Как известно, каждый i -й газовый компонент находится в смеси при температуре
Тi = Тсм, где Тсм – температура газовой смеси. Если теперь мысленно из смеси убрать все газовые компоненты за исключением рассматриваемого компонента, то последний, занимая весь объём смеси Vсм, соответственно будет находиться в разряжённом состоянии под давлением РП,i более низким, чем то, под которым находилась газовая смесь, то есть РП,i < Рсм, где Рсм – абсолютное давление рассматриваемой газовой смеси. Это давление РП,i получило название парциального давления. Таким образом, парциальное давление газового компонентаРП,i – это часть абсолютного давления газовой смеси Рсм, под которым будет находиться данный компонент при условии, что объём и температура этого компонента будут равны объёму и температуре газовой смеси. Если теперь мысленно изотермически увеличить давление газового компонента РП,i до абсолютного давления газовой смеси, то есть до Рсм, то рассматриваемый газовый компонент уменьшит свой объём с Vсм до некоторой величины VП,i. Этот объём VП,i и будет парциальным или приведённым объёмом. Таким образом, парциальный (приведённый) объём газового компонента VП,i – это часть объёма газовой смеси Vсм, которую будет занимать этот компонент при условии, что его абсолютное давление и температура будут равны абсолютному давлению и температуре смеси, то есть Рсм и Тсм. Первое уравнение (3.2.4) для газовых смесей называется законом Амага.
Вполне очевидно, что:
, а 
. (3.2.4)
[ vд,i ] = дол. ед. или % по объёму (об. %).
Величины VП,i можно легко определить из закона Бойля - Мариотта. Учитывая, что если газовый компонент при постоянной температуре находится под парциальным давлением РП,i, то он занимает объём Vсм, а если он при этой же температуре находиться под давлением Рсм, то он занимает парциальный объём VП,i получаем:
Для смесей с ненарушенной сплошностью (газовые смеси, жидкие растворы, металлические сплавы): Мi = Vi(Рсм,Тсм)ri(Рсм,Тсм) и
Мсм = Vсм × (Рсм ,Тсм)rсм(Рсм ,Тсм), где Рсм, Тсм – абсолютное давление, Па, под которым находится смесь и абсолютная температура, К, этой смеси. Учитывая это, а также (2.2.27) получим взаимосвязь между mд,i и vд,i в следующем виде:
(3.2.7)
где 
плотность i-го компонента и смеси при текущих, кг/м3, и нормальных, кг/нор. м3, физических условиях.
Если воспользоваться понятием молярной массы газовой смеси 
, то, уравнение (3.2.7) для смеси идеальных газов, которая сама является идеальным газом, можно преобразовать к виду:
, (3.2.10)
где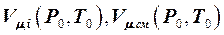 
-молярный объём i-го идеального газа и смеси идеальных газов при нормальных физических условиях, 
молярная масса i-го идеального газа и молярнаямасса смеси идеальных газов, кг/кмоль.
Молярный состав определяется в молярных долях.
Молярная доля mд,i i-го компонента в смеси - отношение количества вещества nm , i этого компонента к общему количеству вещества смеси nm , см:
. (3.2.11)
Вполне очевидно, что:
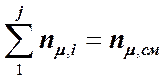, и 
. (3.2.12)
[ mд,i ] = дол. ед. или мол. %.
Количество вещества может быть определено как отношение объёма вещества (для газовых смесей парциального объёма) к его молярному объёму или массы вещества к его молярной массе, то есть:
и 
. (3.2.13)
где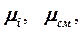 
-молярная масса, кг/кмоль, имолярный объём, м3/кмоль, соответственно i -гокомпонента и смеси.
Учитывая (3.2.11) и (3.2.13), получим взаимосвязи между молярными, объёмными и массовыми долями:
и 
. (3.2.14)
Для смеси идеальных газов 
. Поэтому
mд,i = vд,i, то есть в смесях идеальных газов молярные и объёмные доли численно равны. Следовательно,имеем 
.
Помимо рассмотренных выше показателей, численно характеризующих составы смесей, в технической литературе встречаются и другие показатели.
Закон Дальтона для газовых смесей
Доказывается элементарно. Учитывая, что , получаем:
Плотность, удельный объём и молярная масса смесей
и 
. (3.4.1)
Но 
. Заменив в левой и правой частях этого уравнения Мсм и Мi на произведения соответственно rсмVсм и riVi и разделив обе эти части на Vсм, получим:
где vi(Рсм, Тсм)=1/ri(Рсм, Тсм) – удельный объём i -го компонента, м3/кг.
При известном составе смеси в массовых долях rсм определяется следующим образом:
Соответственно:
. (3.4.5)
Выражения для расчёта величин mсм:
. (3.4.7)
Как показано выше, в газовых смесях 
. Поэтому для них:
(3.4.8)
Величину mсм для газовых смесей можно также определять их термического уравнения состояния идеального газа для произвольной массы газа:
, (3.4.9)
где 
- абсолютное давление, Па, и температура, К, газовой смеси.
Тогда:
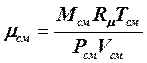. (3.4.10)
Удельная газовая постоянная газовых смесей
Напишем систему уравнений Клапейрона в виде (2.2.8) для всех газовых компонентов при Т = Тсм и Р = Рсм. При этом учтём, что при Т = Тсм и Р = Рсм каждый газовый компонент занимает в смеси парциальный объём VП,i:
(3.5.1)
где 
- парциальные объёмы, м3, массы, кг, и удельные газовые постоянные, Дж/(кг×К), газовых компонентов.
Суммируя левые и правые части всех уравнений этой системы, получим:
, (3.5.2)
или:
. (3.5.3)
Учитывая, что смесь идеальных газов сама является идеальным газом, запишем для газовой смеси уравнение Клапейрона в виде:
. (3.5.4)
Приравняв правые части (3.5.3) и (3.5.4), получим:
. (3.5.5)
Приведённые плотность и удельный объём
компонентов в смеси
По определению приведённая плотность (для газовых смесей чаще используется термин парциальная плотность) i -го компонента rпр,i в смеси есть масса этого компонента Мi, отнесённая к единице объёма смеси Vсм(Рсм,Тсм), а его приведённый (парциальный) удельный объёмvпр,i - объём смеси, отнесённый к единице массы i -го компонента:
. (3.6.1)
Учитывая, что 
и разделив левую и правую части этого уравнения на Vсм(Рсм,Тсм), получим:
или 
(3.6.2)
и далее:
. (3.6.3)
Учитывая, что объём i -го компонента в газовой смеси равен объёму смеси Vсм, когда он находится под парциальным давлением РП,i, получаем, что rпр,i (Рсм,Тсм) и vпр,i (Рсм,Тсм) будут плотностью и удельным объёмом этого компонента при Р = РП,i. и Т = Тсм, то есть в газовых смесях
rпр,i (Рсм,Тсм) = ri (РП,i,Тсм) и vпр,i (Рсм,Тсм) = vi (РП,i,Тсм). Поэтому приведённые (парциальные) плотности и удельные объёмы газовых компонентов можно легко найти, используя уравнение Клапейрона:
.
