Теплопередача. Основные уравнения теплопередачи. Передачи тепла через плоскую стенку.

Лекция №11

Плоская стенка

Рассмотрим сложный процесс передачи тепла через плоскую стенку от горячего теплоносителя к холодному. Характер изменения температур показан на рис. 11-2. В слое горячего теплоносителя температура изменяется от Т до 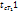по толщине стенки — от t cт1. до t cт.2, и в слое холод­ного теплоносителя от tст2. до t.

Напишем уравнения передачи тепла конвекцией от горячего теплоносителя к стенке, путем теплопроводности через стенку и конвекцией от стен­ки к холодному теплоносителю:

 

где — коэффициенты теплоотдачи от горячего теплоносителя к стенке и от F стенкн к холодному теплоносителю.

Поверхность теплообмена F равна поверхности стенки и при плоской стенке является постоянной величиной.

При установившемся процессе количества тепла, передаваемые от горячего теплоносителя к стенке Q1, через стенку Q cт и от стенки к холодному теплоносителю Q2, должны быть равны между собой, т. е.

Q1=Qcт=Q1=Q

Определим из уравнений (А) частные температурные на­поры:

(Б)

=

=

=

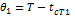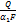
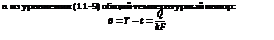Отношение представляющее собой количество тепла, передаваемое в единицу времени через единицу поверхности, на­зывают удельной тепловой нагрузкой, или плотностью теплового потока (размерность — вт/м'^г).

Величины и/ 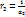-,обратные коэффициентам теплоотдачи, называют тепловыми (термическими) сопротивлениями при переходе тепла через пограничный слой теплоносителя.

Аналогично 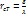- будет тепловым сопротивлением стенки,

а общим тепловым сопротивлением при переходе тепла от одного теплоносителя к другому. Размерность теплового сопротивления — м ² • град/вт.

Вводя удельную тепловую нагрузку и тепловые сопротивления, уравнения (Б) можно написать в виде

(Г)

а уравнение (В) в форме

(Д)

Так как общий температурный напор равен, очевидно, сумме частных температурных напоров (см. рнс. 11-2):

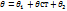
то, подставляя значения нз уравнений (П и (Д), после сокращения на q получим:

(Е)

т. е. общее тепловое сопротивление равно сумме всех частных тепловых сопротивлений.

Подставляя приведенные выше значения тепловых сопротивлений в уравнение (Е), находим

+

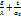
Или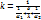

( 11 - 12 )

Это уравнение является весьма важным, так как позволяет вычислить значение коэффициента теплопередачи к, если известны коэффициенты теплоотдачи н обоих теплоносителей, а также толщина и теплопроводность разделяющей их стенки.

Если стенка состоит из нескольких слоев

В этом случае уравнение (11-12) примет следующий вид:

11-13)

Обратимся снова к уравнению (Е). Из него видно, что полное тепловое сопротивление всегда больше каждого из слагаемых:

 

 

Подставляя значения тепловых сопротивлений, получим:

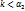
Соответственно для обратных величин имеем:

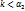
т. е. коэффициент теплопередачи k всегда меньше любого из коэффициентов теплоотдачи

(11-14)