Пример. Число 
перевести в двоичную систему счисления.
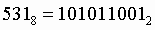
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число 
перевести в двоичную систему счисления.
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1. Число 
перевести в восьмеричную систему счисления.
Пример 2. Число 
перевести в шестнадцатеричную систему счисления.
Перевод дробной части
При переводе дробной части, в отличие от перевода целой части - нужно не делить, а умножать на основание той системы счисления, в которую мы переводим. При этом каждый раз отбрасываются целые части, а дробные части - снова умножаются. Собрав целые части в том порядке, как они были получены - получается дробная часть числа в нужной системе счисления.
Одна операция умножения даёт ровно один дополнительный знак в системе счисления, в которую осуществляется перевод.
При этом существует два условия завершения процесса:
1) в результате очередного умножения Вы получили ноль в дробной части. Понятно, что дальше этот ноль сколько ни умножай - он всё равно останется нулём. Это означает, что число перевелось из десятичной системы счисления в нужную точно.
2) не все числа возможно перевести точно. В таком случае обычно переводят с некоторой точностью. При этом сначала определяют, сколько знаков после запятой будет нужно - именно такое количество раз и нужно будет выполнить операцию умножения.
Вот пример перевода числа 0.3910 в двоичную систему счисления. Точность - 8 разрядов (в данном случае точность перевода выбрана произвольно):
Если выписать целые части в прямом порядке, то получим 0.3910=0.011000112.
Самый первый ноль (на рисунке перечёркнут синим) выписывать не нужно - так как он относится не к дробной части, а к целой. Некоторые по ошибке записывают этот ноль после запятой, когда выписывают результат.
Вот так будет выглядеть перевод числа 0.3910 в шестнадцатеричную систему счисления. Точность - 8 разрядов в данном случае точность снова выбрана произвольно:
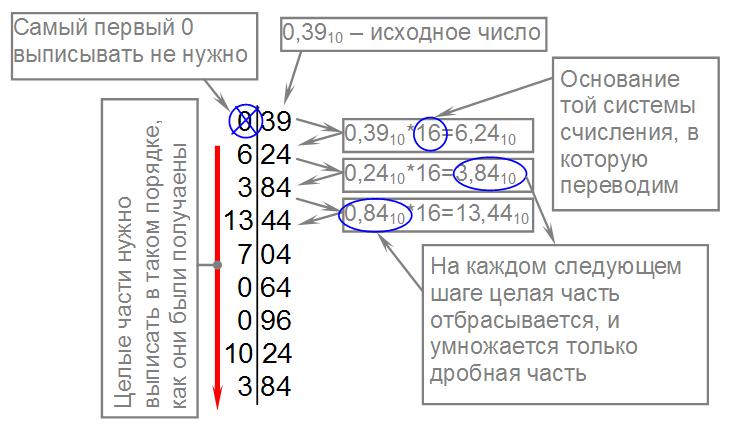
Если выписать целые части в прямом порядке, то получим 0.3910=0.63D700A316.
При этом Вы, наверное, заметили, что целые части при умножении получаются в десятичной системе счисления. Эти целые части, полученные при переводе дробной части числа следует интерпретировать точно так же, как и остатки при переводе целой части числа. То есть, если при переводе в шестнадцатеричную систему счисления целые части получились в таком порядке: 3, 13, 7, 10, то соответствующее число будет равно 0.3D7A16.
Контрольные вопросы:
1. Что такое система счисления?
2. Чем отличается позиционная от непозиционной системы счисления?
3. Приведите пример позиционной системы счисления.
4. Что такое основание позиционной системы счисления?
5. Какие системы счисления используются в ЭВМ?
