от отношения b = Р2/Р1
При 
результаты опытов полностью совпадают с результатами расчётов по уравнению (8.3.19). При Р 2 = Р 1, естественно Мt, г = 0. С уменьшением абсолютного давления среды Рср, а соответственно и Р 2, расход газа увеличивается и достигает максимального значения Мt,г , max при Р 2/ Р 1= bкр. При дальнейшем уменьшении Р 2/ Р 1= b значение Мt, г, рассчитанное по уравнению (8.3.19), убывает и в конечном итоге становится равным нулю. В действительности же Мt, г при Р 2/ Р 1 < b кр остаётся постоянным (прямая КД).
Для объяснения противоречия между выводами теории и опытными данными А. Сен-Венан в 1839 г. выдвинул следующую гипотезу.
Для значений b кр < Р 2/ Р 1 < 1 абсолютное давление в устье суживающегося сопла Р 2 равно абсолютному давлению среды Рср, куда происходит истечение газа, Р 2 = Р ср. Поэтому теория совпадает с опытными данными. Этот режим истечения газа назвали докритическим режимом истечения. Соответственно при этом режиме используется весь перепад давления от Р 1 до Р 2 = Рср и происходит полное расширение газа непосредственно в суживающемся сопле. В этом случае в процессе истечения газа реализуется вся потенциальная энергия сжатого газа (располагаемая работа) на обеспечения скорости истечения. Соответственно расчёт величины w2 осуществляется по формулам: (8.3.1), (8.3.2), (8.3.3), (8.3.5), (8.3.6), (8.3.14), (8.3.15), а Мt, г по формулам (8.3.18) или (8.3.19)
При 0 < Р 2/ Р 1 < bкр абсолютное давление в устье суживающегося сопла перестаёт быть равным давлению среды и даже при понижении Р ср до нуля (полный вакуум) Р 2 остаётся постоянным. Этот режим назвали критическим режимом истечения, а параметры, при которых он возникает, назвали критическими параметрами (Внимание! Не путать эти параметры с критическими параметрами, критические абсолютная температура Т кр и абсолютное давление Р кр , при которых газы и пары жидкостей находятся в критическом состоянии). При этом режиме используется уже не весь перепад давления от Р 1 до Р 2, а только часть его от Р 1 до Р ¢кр > Р 2, то есть происходит неполное расширение газа непосредственно в сопле. Величина Р¢кр соответственно определяется следующим образов Р¢кр = bкрР 1.
Чтобы найти b кр, при котором Мt, г = Мt, г , max, необходимо продифференцировать (8.3.19) по переменной b и приравнять к нулю полученную первую производную:
. (8.4.1)
Анализ (8.4.1) показывает, что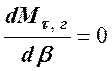 
только при
.
Найдём последнюю производную и приравняем её к нулю:
. (8.4.2)
Разделив уменьшаемое и вычитаемое полученной производной на 
и произведя соответствующие преобразования, получим:
(8.4.3)
Отношение b, определяемое по формуле (8.4.3), называется критическим отношением абсолютных давлений газа на выходе из сопла и на входе в него обозначается как b кр. Абсолютное давление на выходе (срезе) из сопла, которому соответствует это отношение, называется критическим давлением Р¢ кр:
(8.4.4)
Анализ (8.4.4) показывает, что величина bкр зависит только от показателя адиабаты k (показателя изоэнтропы пиз), то есть от природы газа.
Таким образом, максимальная скорость истечения газа в окружающую среду будет тогда, когда абсолютное давление на срезе простого сопла (суживающегося, цилиндрического, расширяющегося) будет равно абсолютному давлению этой среды, то есть Р 2 = Рср. При равенстве этих давлений докритический режим истечения газа переходит в критический и параметры истечения уже необходимо рассчитывать по другим формулам
Уравнение (8.4.4) даёт абсолютное давление в выходном сечении сопла Р¢кр, обеспечивающее теоретический максимальный расход Мt, г , а соответственно и теоретическую максимальную скорость истечения газа из суживающегося сопла wmax. Это критическое давление есть наименьшее абсолютное давление, которое устанавливается в выходном сечении суживающегося сопла.
Величину Мt, г , max можно определить из уравнения (8.3.19), заменив в них отношение Р 2/ Р 1 на bкр из (8.4.4). При bкр имеет место максимально возможная скорость истечения газа (ниже будет показано, что она численно равняется wзв). Она одинакова и при w 1 = 0, и при w 1 > 0. Поэтому при расчётах
Мt, г , max начальную скорость газа учитывать не надо. При очень большой w 1 уже на начальных участках суживающегося сопла скорость истечения газа в принципе может достигнуть величины wз в. Однако в этом случае следующие участки суживающегося сопла становятся диффузором и соответственно будут способствовать уменьшению скорости движения газа. Соответственно получаем:
Если пренебречь влиянием температуры на величину k, то, подставляя в эту формулу значение k, получаем для двухатомных газов (k » 1,40) формулу для приближённых расчётов величины Мt, г ,max следующего вида:
(8.4.6)
Для трёхатомных газов (k » 1,33) эта формула принимает вид:
(8.4.7)
Анализ (8.4.5) показывает, что Мt, г , max определяется только начальным состоянием газа, то есть его Р 1 и v 1, а также величиной S 2 и природой газа, то есть показателем адиабаты k (показателем изоэнтропы пиз).
Скорость газа, которая устанавливается в выходном сечении суживающегося сопла при истечении газа в окружающую среду с абсолютным давлением Рср, равным или ниже Р¢кр, называется критической скоростью wкр.
Величину wкр можно определить из уравнения (8.3.15), заменив в нём отношение Р 2/ Р 1 на b кр из (8.4.4).
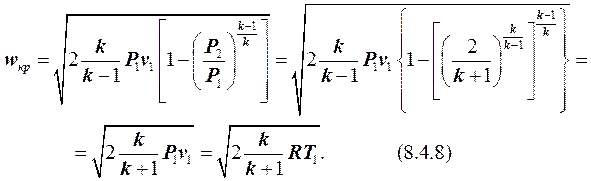
Анализ (8.4.8) показывает, что величина wкр определяется также только начальными параметрами газа Р 1, v 1, Т 1 и его природой k или пиз. Согласно опытным данным, ориентировочно можно считать, что для получения wкр достаточно иметь Р 1, в два раза большее, чем Р ср.
Пренебрегая влиянием температуры на величину k, можно получить следующие формулы для приближённых расчётов величин wкр:
для двухатомных газов: 
для трёхатомных газов: 
Критическая скорость истечения газа из суживающегося сопла wкр равна местной скорости звука в газе при критических параметрах Р¢ кр и v¢ кр, где v¢ кр – удельный объём газа при критической скорости истечения, м3/кг.
Из уравнения адиабатного процесса следует:
. (8.4.9)
Из уравнения (8.4.4) получим:
(8.4.10)
Подставив (8.4.10) в (8.4.9), получаем:
(8.4.11)
Перемножив почленно (8.4.10) и (8.4.11), получим:
Заменив в (8.4.8) Р 1 v 1 на правую часть (8.4.12), получим:
где Т¢ кр – абсолютная температура газа при критической скорости истечения, К.
Величину Т¢ кр определим из уравнения адиабаты, учитывая уравнение (8.4.4):
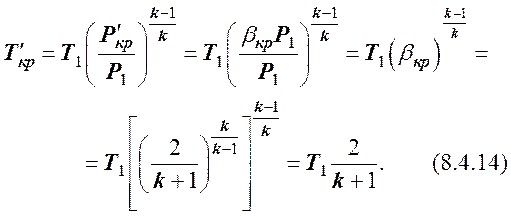
Анализ формулы (8.4.13) показывает, что местная скорость звука в газе wзв для параметров газа, имеющих место в выходном сечении суживающего сопла, действительно равна критической скорости wкр истечения газа из этого сопла. Таким образом, в выходном сечении суживающего сопла при изоэнтропном истечении газа с Р 2 = Р¢кр устанавливается критическая скорость истечения газа, равная местной скорости звука в этом газе при Р = Р¢ кр и v = v¢ кр.
Наличие в выходном сечении суживающегося сопла равенства w кр.= wзв позволяет объяснить, почему в этом сопле газ не может расширяться до абсолютного давления меньше критического Р¢ кр и иметь w кр.> wзв. Из физики известно, что импульсы давления (упругие колебания) распространяются в материальной среде со скоростью звука. Поэтому, когда скорость истечения газа w 2 меньше скорости звука, уменьшение внешнего абсолютного давления среды Р ср, в которую истекает газ, передаётся по потоку газа внутрь сопла с относительной скоростью (wзв. - w 2) и приводит к перераспределению абсолютного давления в сопле. В результате в выходном сечении суживающегося сопла устанавливается давление равное давлению среды (Р 2 = Р ср) и при уменьшении Р ср разность (Р 1 - Р 2) увеличивается, что приводит к росту w 2. Для того чтобы полностью расширить газ до абсолютного давления среды, чтобы
Р 2 = Р ср (так называемый расчётный режим работы сопла), нужно при
Р 2 > Р кр сопло делать суживающимся. Если же в суживающемся сопле будет Р' кр > Р 2, то газ в конечном итоге всё равно будет расширяться от Р' кр до Р ср, однако это произойдёт за пределами сопла (нерасчётный режим работы сопла) и кинетическая энергия газа E к уже полностью не может быть использована для получения полезной работы.
Если же скорость истечения w 2 достигает местной скорости звука wзв, то есть критической скорости истечения wкр, то в этом случае волна разряжения, которая возникает при уменьшении абсолютного давления среды Р ср, не может распространиться против течения потока газа в сопле, так как в этом относительная скорость [ wзв, - (w 2 = wкр)] = 0. Поэтому никакого перераспределения абсолютного давления в сопле не происходит и в его выходном сечении всегда Р 2 остаётся постоянным, независимо от величины Р ср. Таким образом, в этом случае при любом Рср. £ Р'кр. имеет место (Р 2 = Р' кр) – Р 1 = const и
w 2 = wкр = const.
Таким образом, режим истечения газа в окружающую среду, а соответственно и расчётные формулы, определяется из соотношения величин b и b кр, которые определяются как:
и 
.
При b < bкр, то есть 
, то расчёт параметров истечения осуществляется по основным формулам (8.4.5) и (8.4.8), а соответственно и другим, полученным на их основе.
Получение сверхзвуковых скоростей истечения газов
При наличии достаточно большого перепада давлений в сопле, то есть при достаточно малых отношениях 
, можно получить скорость истечения газа w 2, превышающую скорость звука wзв. Однако для этого нужно применять сопла особой конфигурации.
Для достижения в сопле сверхзвуковой скорости его сечение должно изменяться (по ходу газа) следующим образом. Вначале, когда скорость газа нарастает от некоторого минимального значения, сечение сопла должно уменьшатся, то есть канал должен быть суживающимся (dS с < 0). В том месте, где достигается wзв, сопло должно иметь минимальное постоянное сечение
(dS с = 0). Как только wзв будет достигнута, дляполучения сверхзвуковой скорости последующая часть канала должна быть расширяющаяся. Чтобы получить на выходе из расширяющейся части канала сверхзвуковую скорость, нужно получить на выходе из него давление меньше критического, то есть Р 2 < Р кр. В идеале необходимо обеспечить равенство Р 2 = Р ср, что обеспечит так называемый расчётный режим работы сопла, при котором будут минимальные потери энергии.
Наиболее простое сопло, в котором возможно получение сверхзвуковой скорости истечения газа, есть комбинированное сопло Лаваля простой конической формы (часто называют просто соплом Лаваля). Оно названо в честь шведского инженера, предложившего это сопло для получения сверхзвуковых скоростей истечения водяного пара, направляемого в паровую турбину. Форма этого сопла положена в основу сопел применяющихся в ракетных и реактивных двигателях, что обеспечивает сверхзвуковые скорости движения ракет и самолётов. Соответственно сопло Лаваля состоит из конических сужающейся и расширяющейся частей.
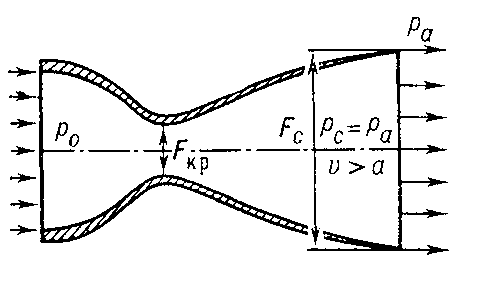
Схема сверхзвукового сопла (сопла Лаваля)
Поток газа в расширяющейся части сопла находится в особых условиях, связанных с тем, что здесь скорость частиц газа больше, чем скорость распространения в газе волны давления, вызванной действием абсолютного давления во внешней среде Р ср. Поскольку влияние Р ср не может распространиться вверх по потоку, то это давление не оказывает влияния на движение газа в расширяющейся части сопла. Оно оказывает влияние лишь в начале движения газа; если это давление больше критического, то поток не станет сверхзвуковым, если же меньше, то после узкого сечения поток становится сверхзвуковым и «выходит из-под контроля» Р ср.
Увеличение сечения канала соответственно приводит к уменьшению абсолютного давления в газе и к его расширению, вследствие чего скорость газа увеличивается. Начиная от минимального сечения сопла, параметры газа во всех последующих сечениях, в том числе и в выходном, зависят только от значения параметров в этом минимальном сечении и от степени расширения сопла, то есть от отношения площади выходного сечения S 2 к площади минимального сечения.
Увеличивая площадь S 2 при постоянных начальных параметрах газа, можно осуществить более глубокое расширение газа и увеличить скорость истечения w 2. Однако при этом абсолютное давление в выходном сечении Р 2 не должно быть меньше Р ср, так как в этом случае возникает так называемый нерасчётный режим работы сопла, характеризующийся увеличением неравновесности процесса истечения газа из сопла.
Таким образом, при истечении газа через сопло Лаваля в окружающую среду с давлением Р ср меньше критического Р кр в суживающей части этого сопла скорость газа w увеличивается от w 1 = 0 (истечение газа из сосуда неограниченной ёмкости) или от w 1 > 0 (истечение газа из сосуда ограниченной ёмкости) до критической скорости w кр, равной местной скорости звука w зв. Равенство выполняется в самой узкой части сопла Лаваля, которое называется критическим сечением этого сопла. Соответственно параметры газа, которые имеют место в этом сечении, называется критическими. Методы их расчёта рассмотрены выше.
В расширяющейся части сопла Лаваля происходит дальнейшее увеличение w газа и падение его абсолютного давления. В выходном сечении сопла w 2 > w зв и абсолютное давление газа Р 2 = Р ср (расчётный режим работы сопла).
Таким образом, расширяющаяся часть сопла Лаваля создаёт условия для получения сверхзвукового потока, которые не могут быть созданы только понижением абсолютного давления в среде Р ср, куда происходит истечение газа.
Профилированием проточной части сопла Лаваля достигается лишь различное распределение абсолютного давления газа внутри сопла, но его массовый расход при этом в выходном сечении всегда остаётся постоянным.
Расчёты скорости истечения газа на выходе из сопла Лаваля и массового расхода газа осуществляются по формулам (8.4.8) и (8.4.5), рассмотренным выше.
