Электрические цепи трехфазного тока.
Трехфазная система
Многофазной системой называется совокупность, состоящая из ” n ” отдельных одинаковых электрических цепей или электрических схем, режимные параметры в которых (е, u, i) сдвинуты во времени на равные отрезки 
или по фазе 
.
Отдельные части системы называются фазами. Термин ”фаза” в электротехнике имеет два смысловых значения: первое - как момент времени для синусоидальной функции тока или напряжения, второе - как часть многофазной системы. В технике нашли применение 2-х, 3-х, 6-и и более фазные системы. В электроэнергетике наибольшее распространение получила трехфазная система, обладающая рядом преимуществ перед системами с другим числом фаз.
Трехфазная система состоит из трех электрических цепей или электрических схем (фаз), параметры режима (u,i) в которых сдвинуты во времени на 
. Отдельные фазы трехфазной системы согласно ГОСТ обозначаются (именуются) заглавными латинскими буквами А, В, С (основное обозначение), или цифрами 1, 2, 3 (допустимое обозначение), или заглавными латинскими буквами R, S, T (международное обозначение).
 |
Не имеет значения, какую из трех фаз именовать какой буквой А, В или С, существенным является их порядок следования друг за другом во времени. Прямым порядком следования фаз называется А 
В С А, при котором параметры режима (u, i) в фазе В отстают от аналогичных параметров в фазе А на 120o, а в фазе С - опережают на 120o. При обратном порядке следования фаз А С В А параметры режима в фазе С отстают от аналогичных параметров в фазе А на 120o, а в фазе В - опережают на 120o. 
Если отдельные фазы системы работают изолировано и независимо друг от друга, то система называется несвязанной. Рассмотрим работу простейшей несвязанной трехфазной системы (рис. 85). Мгновенные значения фазных ЭДС генератора сдвинуты во времени на 120o в порядке следования фаз A ® B ® C ® A:
;
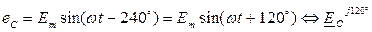
Графические диаграммы этих функций показаны на рис. 86, а векторные - на рис. 87.
 |
 |
Основное свойство любых переменных функций (е, u, i) в симметричной трехфазной системе состоит в том, что сумма их мгновенных значений в любой момент времени равна нулю, например, еА + еВ + еС = 0. Найдем эту сумму для разных моментов времени:
, 
;
, 
;
, 
.
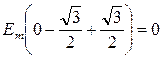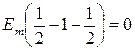Как следует из векторной диаграммы рис. 87, геометрическая сумма векторов фазных ЭДС также равна нулю:
.
Если нагрузка отдельных фаз равна между собой, т.е. 
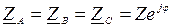, то фазные токи будут равны по модулю и сдвинуты по фазе относительно своих ЭДС (напряжений) на один и тот же угол φ, а между собой, как и ЭДС, будут сдвинуты по фазе на 120о. Следовательно, фазные токи iА, iВ, iС образуют симметричную трехфазную систему и для них будут справедливы полученные ранее выводы: iА + iВ + iС = 0; I А + I В + I С = 0.
Преобразуем несвязанную трехфазную систему рис. 1 в связанную путем объединения трех обратных приводов в один общий привод. Согласно 1-ому закону Кирхгофа в общем проводе должен протекать суммарный ток iN = iА + iВ + iC = 0. Это означает, что потребность в обратном проводе вообще отпадает, благодаря чему достигается значительная экономия проводов при передаче энергии от трехфазного генератора к приемнику.
Достоинства трехфазной системы:
1) Передача энергии от генератора к потребителям трехфазным током наиболее выгодна экономически, чем при любом другом числе фаз. Например, по сравнению с двухпроводной системой достигается экономия проводов в два раза (3 провода вместо 6), соответственно уменьшаются потери энергии в проводах линии.
2) Трехфазная система позволяет технически просто получить круговое вращающееся поле, которое лежит в основе работы всех трехфазных машин (генераторов и двигателей).
3) Элементы трехфазной системы (генераторы, трансформаторы, двигатели) просты по конструкции, надежны в работе, имеют хорошие массогабаритные показатели, сравнительно дешевы, долговечны.
4) На выходе трехфазных генераторов имеется два уровня выходного напряжения – линейное и фазное, отличающиеся в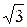 
раз (U л / U ф = 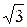), что позволяет подключать к такому генератору приемники с различными номинальными напряжениями.
Благодаря своим достоинствам трехфазная система применяется в электроэнергетике для производства, передачи, распределения и потребления электрической энергии.
Трехфазная система и ее основные звенья – генератор, трансформатор, линия электропередачи, двигатель – были разработаны в 1889 году инженером Доливо-Добровольским (фирма Сименс и Шукерт). Создание этой системы явилось важным событием в истории развития теоретической и прикладной электротехники.
Способы соединения обмоток трехфазных генераторов
В обмотках трехфазного генератора индуктируются синусоидальные ЭДС, сдвинутые по фазе на 1200:
,
,
,
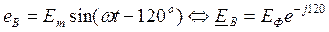Между собой фазные обмотки генератора могут соединяться по двум различным схемам: звездой (
) и треугольником (
).
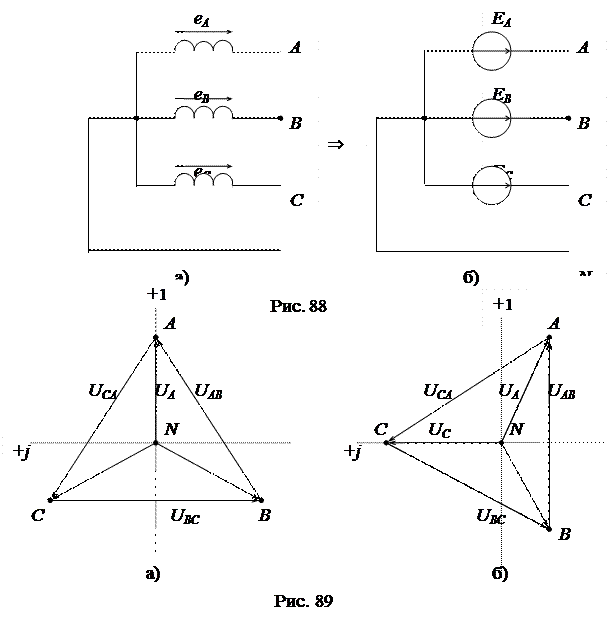
При соединении в звезду концы фазных обмоток (фаз) генератора соединяются в общую точку N, которая называется нулевой или нейтральной, а начала обмоток служат линейными выводами генератора А, В, С (рис. 88).
Векторная диаграмма напряжений трехфазного генератора при соединении его фазных обмоток в звезду показана на рис. 89а, б.
В трехфазном генераторе различают фазные и линейные напряжения. Фазными называются напряжения между началами и концами фазных обмоток или между одним из линейных выводов А, В, С и нулевым выводом N. Фазные напряжения равны фазным ЭДС: U А= Е А, U В= Е В, U С= Е С (индекс N при фазных напряжениях опускается, так как φN = 0). Линейными называются напряжения между двумя линейными выводами А, В, С. Линейные напряжения равны векторной разности двух фазных напряжений: U АВ = U А - U В; U ВС = U В - U С; U СА = U С - U А.
 |
При расчете трехфазных цепей комплексным методом фазные и линейные напряжения генератора представляются в комплексной форме, при этом один из векторов системы принимают за начальный и совмещают его с вещественной осью, а остальные вектора получают начальные фазы согласно их углам сдвига по отношению к начальному вектору. На рис. 89а показан вариант представления напряжений трехфазного генератора в комплексной форме, когда за начальный вектор принимается фазное напряжение фазы А. В этом случае фазные напряжения генератора в комплексной форме получат вид: 
, 
, 
, линейные напряжения: 
, 
, 
.
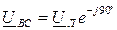На рис. 89б показан другой вариант представления напряжений трехфазного генератора в комплексной форме, когда за начальный вектор принимается линейное напряжение U AB. В этом случае фазные напряжения генератора в комплексной форме получат вид: 
, 
, 
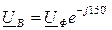, линейные напряжения: 
, 
, 
.
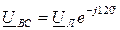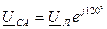Из геометрии рис. 5 получаем соотношение между модулями линейного и фазного напряжений: UЛ = 2 UФ cos 300 =2 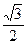UФ 
= 
UФ.
Обмотки трехфазного генератора теоретически можно включать по схеме треугольника. В такой схеме конец каждой предыдущей фазы соединяется с началом последующей, а точки соединения служат линейными выводами генератора (рис. 90).
 |
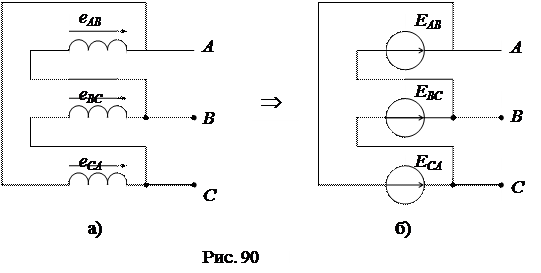При соединении фаз в треугольник в его контуре действует сумма фазных ЭДС: 
= еАВ + еВС + еСА. В реальных трехфазных генераторах технически невозможно обеспечить равенство нулю для суммарной ЭДС. Так как собственные сопротивления обмоток генератора малы, то даже незначительная по величине суммарная ЭДС 
0 может вызвать в контуре треугольника уравнительный ток, соизмеримый с номинальным током генератора, что привело бы к дополнительным потерям энергии и снижению КПД генератора. По этой причине обмотки трехфазных генераторов запрещается соединять по схеме треугольника.
Номинальным напряжением в трехфазной системе называется линейное напряжение. Номинальное напряжение принято выражать в киловольтах (кВ). Шкала номинальных трехфазных напряжений, применяемых на практике, имеет вид: 0,4; 1,1; 3,5; 6,3; 10,5; 22; 35; 63; 110; 220; 330; 500; 750. На потребительском уровне номинальное трехфазное напряжение может указываться в виде отношения U Л ⁄ U Ф, например: U Л ⁄ U Ф = 380 ⁄ 220 В.
