Лекция №6
Представление чисел в компьютере: естественная и нормальная формы. Алгебраическое представление двоичных чисел: прямой, обратный и дополнительный коды.
План
1. Естественная и нормальная формы.
2. Прямой, обратный и дополнительный коды.
1. Представление чисел в компьютере: естественная и нормальная формы.
В ЭВМ применяются две формы представления чисел:
• естественная форма, или форма с фиксированной запятой (точкой) — ФЗ (ФТ);
• нормальная форма, или форма с плавающей запятой (точкой) - ПЗ (ПТ).
Фиксированная запятая (точка). В форме представления с фиксированной запятой (точкой) числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.
Например, пусть числа представлены в десятичной системе счисления и имеют пять разрядов в целой части числа (до запятой) и пять в дробной части (после запятой). Числа, записанные в такую разрядную сетку, имеют вид:
+00721.35500.
+00000.00328.
-10301.20260.
Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому чаще всего неприемлема при вычислениях.
В компьютерах естественная форма представления используется как вспомогательная и только для целых чисел.
В памяти ЭВМ числа с фиксированной точкой хранятся в трех форматах:
а) полуслово — это обычно 16 бит, или 2 байта;
б) слово — 32 бита, или 4 байта;
в) двойное слово — 64 бита, или 8 байтов.
Отрицательные числа с ФТ записываются в разрядную сетку в дополнительных кодах, которые образуются прибавлением единицы к младшему разряду обратного кода. Обратный код получается заменой единиц на нули, а нулей на единицы в прямом двоичном коде.
Плавающая запятая (точка). В форме представления с плавающей запятой (точкой) число изображается в виде двух групп цифр:
• мантисса;
• порядок.
При этом абсолютная величина мантиссы должна быть меньше 1, а порядок должен быть целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:
N=±M*P±r,
где М — мантисса числа (| М\ < 1); r — порядок числа (целое число); Р — основание системы счисления.
Например, приведенные ранее числа в нормальной форме запишутся следующим образом:
+0,721355 *103;
+0,328 * 10-3;
-0,103012026 * 105.
Нормальная форма представления обеспечивает большой диапазон отображения чисел и является основной в современных компьютерах.
Следует заметить, что все числа с плавающей запятой хранятся в машине в так называемом нормализованном виде.
Нормализованным называют такое число, старший разряд мантиссы которого больше нуля. У нормализованных двоичных чисел, следовательно, 0,5 < | М\ < 1.
Нормализованные, т. е. приведенные к правильной дроби, числа:
10,3510= 0,103510 *10+2;
0,000072458=0,72458*8-4;
F5C,9B16=0,F5C9B,6*16+3;
В памяти ЭВМ числа с ПТ хранятся в двух форматах:
• слово — 32 бита, или 4 байта;
• двойное слово — 64 бита, или 8 байт.
Разрядная сетка для чисел с ПТ имеет следующую структуру:
• нулевой разряд — это знак числа (0 — «минус», 1 — «плюс»);
• с 1 по 7 разряд записывается порядок в прямом двоичном коде, пустые разряды заполняются нулями. В первом разряде указывается знак порядка (1 — «плюс» или 0 — «минус»);
• с 8 по 31 (63) указывается мантисса, слева направо без нуля целых в прямом двоичном коде и для отрицательных чисел и пустые разряды заполняются нулями.
2. Алгебраическое представление двоичных чисел: прямой, обратный и дополнительный коды.
При хранении информации в памяти ЭВМ каждый вид хранится в одном разряде памяти, а разряды объединяются в ячейки памяти фиксированного размера. При записи цифр с фиксированной точкой, положение точки фиксируется в определенном месте относительно к разрядам числа. При приставлении числа со знаком для кода, выделяется знаковый разряд (обычно крайний слева) «+» = 0 и «-» = 1 – кодируется.
Прямой код числа.
а = +0101  = 0.0101
= 0.0101
в = -1010  = 1.1010
= 1.1010
Прямой код числа совпадает с записью положительного числа.
Пример:
Рассмотрим однобайтовое представление двоичного числа. Пусть это будет 28(10). В двоичном формате - 0011100(2) (при однобайтовом формате под величину числа отведено 7 разрядов). Двоичное число со знаком будет выглядеть так, как показано на рис. 2.1.

Рис. 2.1. Формат двоичного числа со знаком в прямом коде
а - положительное число; б - отрицательное
Сложение в прямом коде чисел, имеющих одинаковые знаки, достаточно просто: числа складываются, и сумме присваивается знак слагаемых. Значительно более сложным является алгебраическое сложение в прямом коде чисел с разными знаками. В этом случае приходится определять большее по модулю число, производить вычитание модулей и присваивать разности знак большего по модулю числа. Такую операцию значительно проще выполнять, используя обратный и дополнительный коды.
Обратный код числа.
а = +0101  = 0.0101
= 0.0101
Обратный код положительного числа совпадает с прямым кодом.
в = -1010 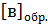 = 1.0101
= 1.0101
Обратный код отрицательного числа образуется так:
1. В знаковом разряде 1.
2. В цифровых разрядах 1 заменяется на 0, а 0 на 1.
Пример:
Вычислить выражение -3(10) -2(10).

Пример:
Вычислить 7(10) -3(10).

Указанные трудности привели к тому, что в современных ЭВМ абсолютное большинство операций выполняется в дополнительном коде.
Дополнительный код числа.
а = +0101  = 0.0101
= 0.0101
Дополнительный код положительного числа совпадает с прямым кодом.
в = -1010  =
= 
Дополнительный код отрицательного числа образуется так:
1. В знаковом разряде 1.
2. В цифровом разряде 1 заменяется на 0, а 0 на 1.
3. К последнему разряду прибавляется 1.
Модифицированный код числа.
Отличается тем, что для изображения знака числа в нем отводится два разряда (положительная кодировка 00, отрицательная 11). Такие коды оказались удобны (с точки зрения построения АЛУ) для выявления переполнения разрядной сетки. Если знаковые разряды результата принимают значение 00 и 11, то переполнения разрядной сетки не было, а если 01 или 10 - то было переполнение.
а = -11001 в = +11001
 = 11.00110
= 11.00110  = 00.11001
= 00.11001
 =
= 
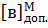 = 00.11001
= 00.11001
Пример:

Контрольные вопросы:
1. Какие две формы представления чисел применяются в ЭВМ?
2. Как изображаются числа в форме с фиксированной запятой (точкой)?
3. Как изображаются числа в форме с плавающей запятой (точкой)?
4. Что такое нормализованное число?
5. В каких двух форматах хранятся числа с плавающей запятой (точкой) в памяти ЭВМ?
6. Приведите примеры записи прямого кода числа для положительных и отрицательных чисел.
7. Как образуется обратный код отрицательного числа?
8. Как образуется дополнительный код отрицательного числа?
9. Чем отличается модифицированный код числа от остальных кодов?






