
Данные:
1.Папортные данные синхронного двигателя шаровой мельницы типа ДМН244-60
| № пп | НАИМЕНОВАНИЕ | Значение | Единица измерения | |
| Мощность | кВт | |||
| Частота вращения | мин –1 | |||
| Напряжение статора | В | |||
| Ток статора | А | |||
| Напряжения на кольцах ротора | В | |||
| Ток возбуждения | А | |||
| Коэффициент мощности | 0,9 | о.е. | ||
| К.П.Д. | 93,3 | % | ||
| Сопротивление фазы обмотки статора при 20 ºС | 0,452 | Ом | 
| |
| Сопротивление обмотки ротора при 20 ºС | 0,582 | Ом | ||
| Система вентиляции | Радиальная | |||
| Предельная допустимая температура охлаждающей среды | ºС | |||
| Предельная допустимая температура обмотки статора | ºС | |||
| Предельная допустимая температура обмотки ротора | ºС |
2.Иммитационная модель СД:
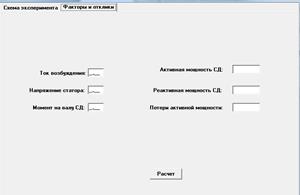
| 2.1«Схема эксперимента» | 2.2«Факторы и отклики» |
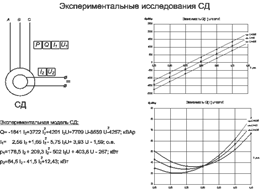
| 
|
3.Данные по варианту №5
| № пп | Количество уровней факторов | Напряжение статора, o.e. | Ток возбуждения, o.e. | Загрузка по активной мощности, о.е. | ||
| Нижнее значение | Верхнее значение | Нижнее значение | Верхнее значение | |||
| 0,96 | 1,04 | 0,5 | 1,1 | 0,5 |
Ход работы:
Зная количество уровней факторов(4 уровня) и имея нижние и верхние значения тока возбуждения(от 0,5 до 1,1(о.е.)) и напряжения статора(от0,96до1,04(о.е.)) найдем факторный шаг для тока и напряжения
1. 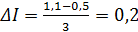

2. 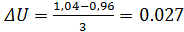

Посчитав колличество экспериментов:
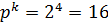 ,
,
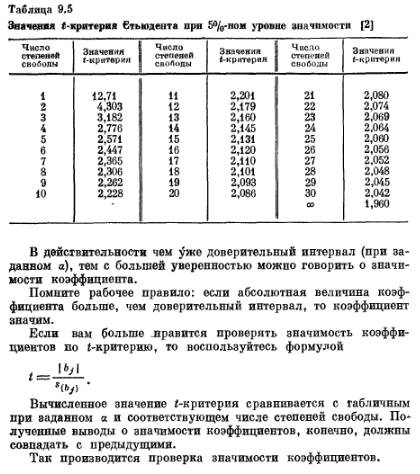
составляем матрицу плана эксперимента(рис.1), проводим эксперименты, и получаем отклики(рис. 2)
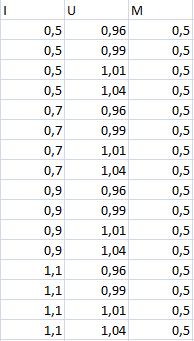
| 
|
| Рисунок 1 – Факторы: I- Ток возбуждения, U - Напряжение статора, M - Загрузка по активной мощности | Рисунок 2 – отклики: P – Активная мощность CД, Q-Реактивная мощность СД, p – Потери активной мощности |
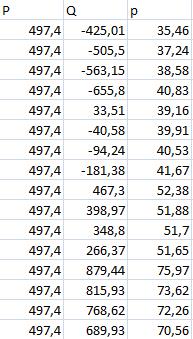
Далее построим график зависимости Реактивной мощности Q от Тока возбуждения I и Напряжения статора U, для этого воспользуемся MS Excel, немного перестроив таблицы факторов и откликов, для того чтобы U было константой.(Рис.3)
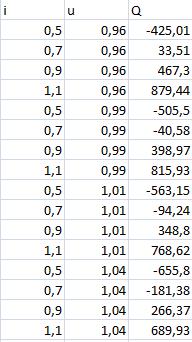
Рисунок 3 - Факторы: i- Ток возбуждения, u - Напряжение статора, Q-Реактивная мощность СД
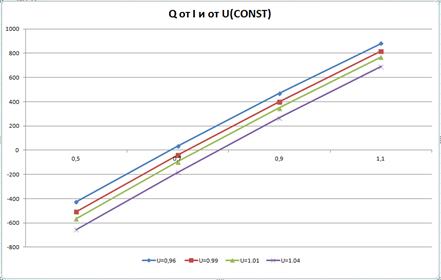
Рисунок 4 – 4 зависимости Q от I, и от U(const)
Получившие зависимости имеют вид «практически» прямых.
Следовательно можем описать их с помощью линейной функции, которая в общем виде записывается:
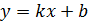 .
.
Для нашего случая нам необходимо как минимум два «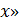 (т.к. нам необходима зависимость Q от I и от U), запишем линейную функцию немного в другом виде:
(т.к. нам необходима зависимость Q от I и от U), запишем линейную функцию немного в другом виде:
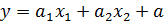 , (1)
, (1)
Где: y - Q-Реактивная мощность СД; 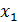 - I- Ток возбуждения;
- I- Ток возбуждения; 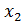 - U - Напряжение статора;
- U - Напряжение статора; 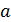 ,
, 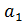 и
и 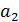 - коэффициенты.
- коэффициенты.
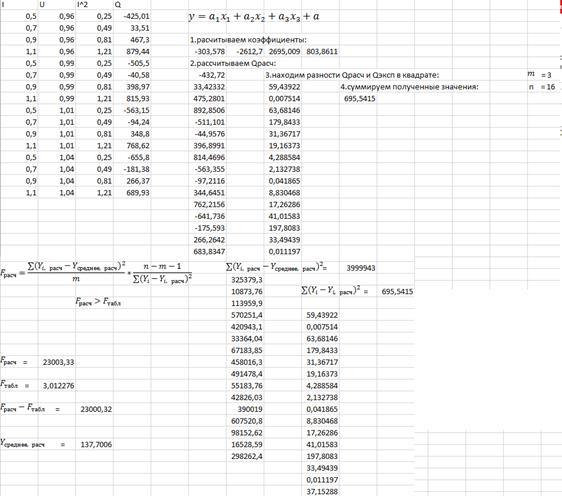
В MS Excel найдем коэффициенты 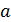 ,
, 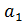 и
и 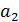 (рис. 5), с помощью функции «ЛИНЕЙН»(она возвращает параметры линейного приближения по методу наименьших квадратов)
(рис. 5), с помощью функции «ЛИНЕЙН»(она возвращает параметры линейного приближения по методу наименьших квадратов)
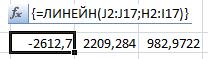
Рисунок 5 - коэффициенты 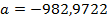 ,
, 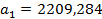 ,
, 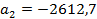
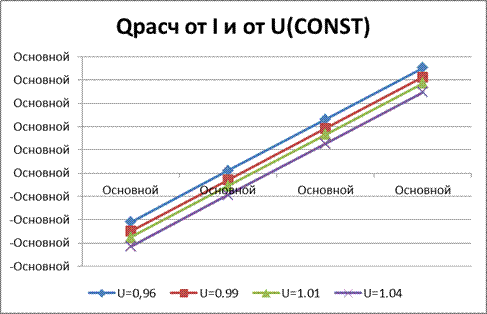
По формуле(1),с помощью найденныйх коэффициентов, в MS Excel рассчитываем Q-Реактивная мощность СД(Рис. 6), и строим полученные зависимости.

| 
|
а) 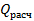
| б) 4 зависимости Qрасч от I, и от U(const) |
Рисунок 6 – а) 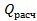 ; б) 4 зависимости Qрасч от I, и от U(const) ; б) 4 зависимости Qрасч от I, и от U(const)
|
Нам нужно проверить адекватность выбраноой функции:
Для начала просто совместим точки полученые эксперементально и расчетные точки, не соединяя их для большей наглядности.
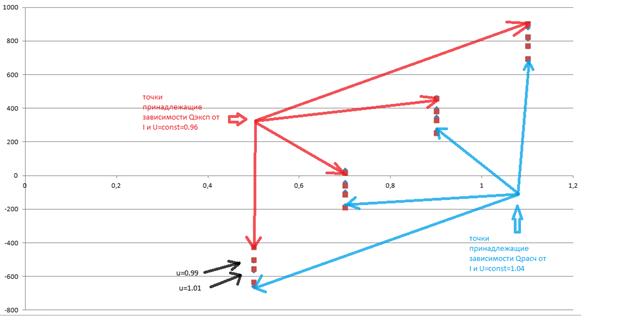
Рисунок 7 – красные точки лежащие на одних диагональных прямых – зависимости Qэксп от I и от U(const), cиние точки лежащие на одних диагональных прямых – зависимости Qрасч от I и от U(const)
Теперь проверим адекватность критерием Фишера:
В общем виде он выглядит вот так:
Модель считается адекватной при условии:
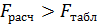 ,
,
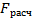 - рассчитывается следующим образом:
- рассчитывается следующим образом:
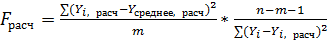 ,
,
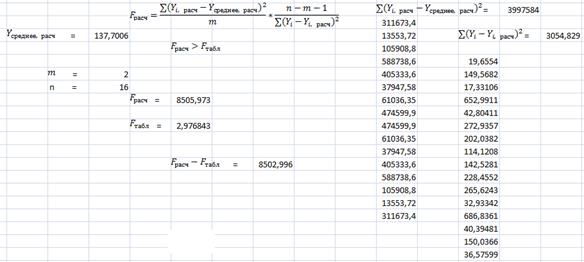
Как мы видим, нашу модель можно назвать адекватной, в связи с тем, что выполняется условие 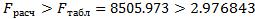
преобразуем формулу (1) в (2), в (3) и в (4) добавив новые переменные, и посмотрим, как будет меняться 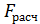 .
.
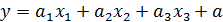 , (2)
, (2)
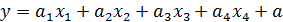 , (3)
, (3)
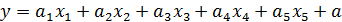 , (4)
, (4)
Где: y = Q-Реактивная мощность СД; 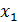 =I- Ток возбуждения;
=I- Ток возбуждения; 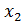 =U - Напряжение статора;
=U - Напряжение статора;  =
= 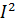 ;
; 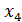 =
= 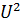 ;
; 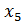 =
= 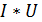 ;
; 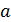 ,
, 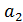 ,
, 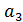 ,
, 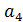 и
и 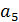 - коэффициенты.
- коэффициенты.
Проделаем все действия приведенные выше:
1)для 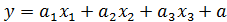 :
:
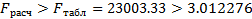 , модель адекватна.
, модель адекватна.
2)для 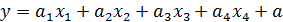

 , модель адекватна
, модель адекватна
3)для 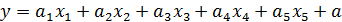

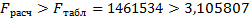 , модель адекватна
, модель адекватна

красные точки лежащие на одних диагональных прямых – зависимости Qэксп от I и от U(const), cиние точки лежащие на одних диагональных прямых – зависимости Qрасч от I и от U(const)
С добавлением новых переменных, уменьшалось отдаление расчетных значений от экспериментальных, на столько, что на представленном(рис. 8) графике, в представленном масштабе, красные и сини точки сливаются.
Вывод: Проверив 4 выше представленные модели на адекватность, выяснили, что все модели с вероятностью 99% адекватны.
Проанализировав модели, выяснили, что Сумма квадратов разности экспериментальной и рассчитанной реактивной мощности синхронного двигателя уменьшалась, по ходу введения в функцию прямой новых переменных (рассчитаная зависимость (Qрасч от I и от U) практически полностью повторяет зависимость (Qэкс от I и от U), полученную экспериментально).




