В данной формуле стоит 2, так как система Малафеева-Порро 1-го рода содержит две призмы!
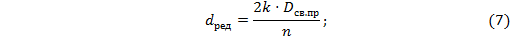
Световой диаметр призмы равен удвоенной высоте верхнего полевого луча, как видно из рисунка:
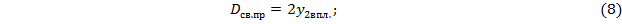
В результате, на основании формул (3),(4),(5),(7) и (8) для определения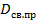 
, имеем выражение:
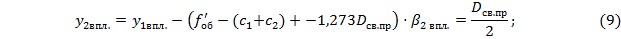
Решим уравнение (9) и определим световой диаметр призмы:
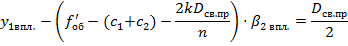
Определив световой диаметр призмы, рассчитаем расстояние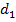 
от главной плоскости объектива до первой входной грани призмы, с учётом формул (5) и (7) имеем:
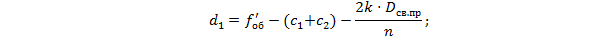
Для уверенности в правильности расчёта 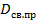, выполним контроль вычислений таким образом, чтобы 
:
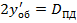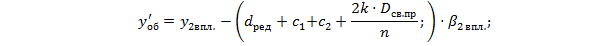
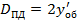, следовательно, 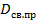вычислен верно.
Расчет светового диаметра призмы для призмы Пехана с крышей и призмы Аббе с крышей:
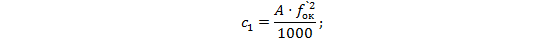
Рассчитаем ход верхнего полевого луча при 50% виньетировании:
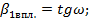
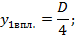
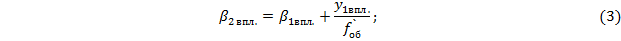
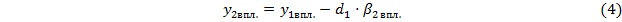
Расстояние 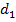от главной плоскости объектива до первой входной грани призмы:
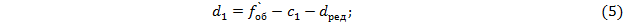
При габаритном расчёте призмы заменяют редуцированными ППП толщиной 
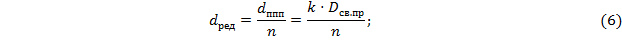
, где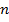 
- показатель преломления стекла призмы(в данном случае это стекло БК10, показатель преломления 
), 
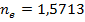- коэффициент призмы (для призмы Пехана с крышей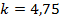 
).
Подставив в формулу (6) значения показателя преломления и коэффициента призмы получим:
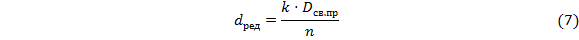
Световой диаметр призмы равен удвоенной высоте верхнего полевого луча, как видно из рисунка:
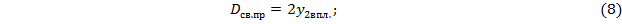
В результате, на основании формул (3),(4),(5),(7) и (8) для определения 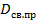, имеем выражение:
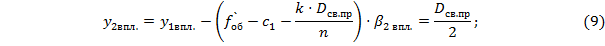
Решим уравнение (9) и определим световой диаметр призмы:
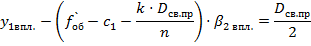
Определив световой диаметр призмы, рассчитаем расстояние 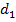от главной плоскости объектива до первой входной грани призмы, с учётом формул (5) и (7) имеем:
Для уверенности в правильности расчёта 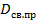, выполним контроль вычислений таким образом, чтобы :
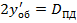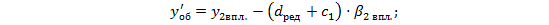
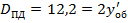, следовательно, 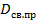вычислен верно
Вопрос: габаритный расчет одной ветви призменного бинокля
Габаритный расчет состоит из двух частей – на первом этапе определяются оптические характеристики объектива и окуляра без призмы;
затем, на втором этапе, рассчитывается световой диаметр призы (призму помещаем на отрезок c1 от ПД) исходя из начальных условий (больше диаметр вх зр или ПД).
Вначале нам необходимо провести габаритный расчёт объектива и окуляра, а затем призмы, представив её в виде ППП толщиной
Габаритный расчет зрительной трубы без призмы.
Сделаем рисунок, на котором представим ход апертурного луча и полевого пучка лучей в системе, состоящей из объектива и окуляра:
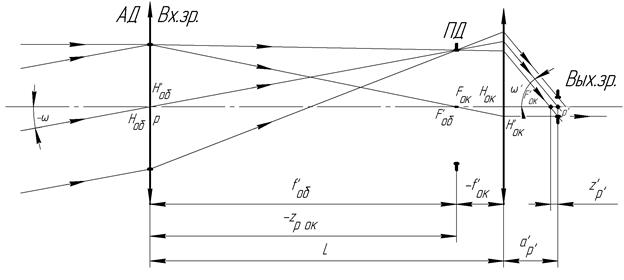
Рисунок 8 – Оптическая схема зрительной трубы Кеплера.
По заданным значениям видимого увеличения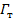 
и длины трубы 
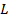определим фокусные расстояния первого и второго компонентов. Для этого запишем и совместно решим два уравнения:
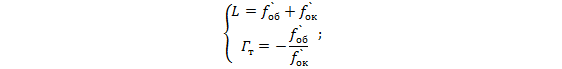
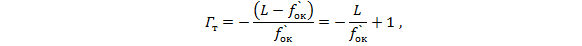
Определим диаметр полевой диафрагмы:
Из рис. 1 видно, что угловое поле окуляра определяет размер полевой диафрагмы:
Диаметр входного зрачка:
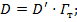
Определим угловое поле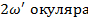 
:
Видимое увеличение 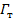определяется по формуле:
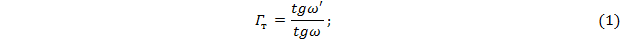
Определим световые диаметры объектива и окуляра
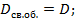
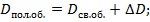
Для вычисления светового диаметра окуляра необходимо определить расстояние от задней главной точки до осевой точки выходного зрачка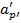 
и расстояние от задней точки фокуса окуляра до осевой точки выходного зрачка 
.
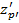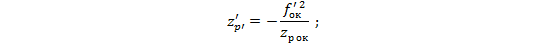
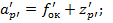
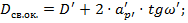
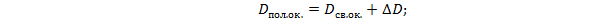
Вопрос: Какое виньетирование в системе призменного бинокля? (см. Рисунок)
Несимметричное виньетирование (это видно из рисунка, лучи неравномерно заполняют плоскость ВД)
Избавиться от него можно, поставив на фронтальную линзу окуляра еще одну ВД.
Вопрос: аберрационный расчет системы, вывод формул для основных аберрационных параметров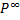 
, 
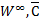
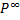- основной аберрационный параметр P, характеризующий сферическую аберрацию
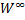- основной аберрационный параметр W(даблвэ!), характеризующий меридиональную кому
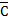– основной хроматический параметр (характеризует хроматизм положения)
В задачу аберрационного расчета входит расчет объектива вместе с призмой. Аберрации системы «объектив + ППП» должны полностью или частично компенсировать аберрации окуляра. В таких системах обычно исправляют сферическую аберрацию, хроматизм положения и меридиональную кому.
Запишем аберрационные уравнения для исправления в зрительной трубе хроматизма положения, сферической аберрации и меридиональной комы:
Уравнение исправления хроматизма положения:
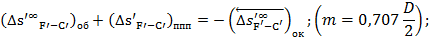
Уравнение исправления сферической аберрации:
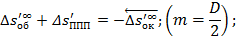
Уравнение исправления меридиональной комы:
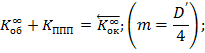
Из распечаток выпишем значения аберраций:
Хроматизм положения:
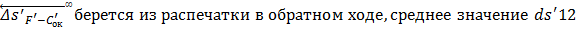
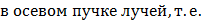
Осевой пучок ____Л0____ ____Л1____ ____Л2____
== M = 100tg б'== dS'=== dY'=== dS'=== dY'=== dS'=== dY'= dS'12 = Eta %=
2.000 13.46 -0.1474-0.0198-0.1390-0.0187-0.1402-0.0188 0.0012 0.0587
1.732 11.63 -0.1103-0.0128-0.1022-0.0119-0.1029-0.0119 0.0007 0.0437
1.414 9.47 -0.0734-0.0070-0.0656-0.0062-0.0657-0.0062 0.0001 0.0289
1.000 6.68 -0.0367-0.0024-0.0291-0.0020-0.0287-0.0019-0.0004 0.0143
0.000 0.00 -0.0000 0.0000 0.0072 0.0000 0.0082 0.0000-0.0009
Продольная сферическая аберрация:
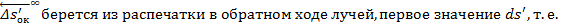
Осевой пучок ____Л0____ ____Л1____ ____Л2____
== M = 100tg б'== dS'=== dY'=== dS'=== dY'=== dS'=== dY'= dS'12 = Eta %=
2.000 13.46 -0.1474 -0.0198-0.1390-0.0187-0.1402-0.0188 0.0012 0.0587
1.732 11.63 -0.1103-0.0128-0.1022-0.0119-0.1029-0.0119 0.0007 0.0437
1.414 9.47 -0.0734-0.0070-0.0656-0.0062-0.0657-0.0062 0.0001 0.0289
1.000 6.68 -0.0367-0.0024-0.0291-0.0020-0.0287-0.0019-0.0004 0.0143
0.000 0.00 -0.0000 0.0000 0.0072 0.0000 0.0082 0.0000-0.0009
Меридиональная кома:
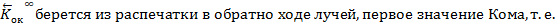
Осевой пучок ____Л0____ ____Л1____ ____Л2____
== M = 100tg б'== dS'=== dY'=== dS'=== dY'=== dS'=== dY'= dS'12 = Eta %=
2.000 13.46 -0.1474-0.0198-0.1390-0.0187-0.1402-0.0188 0.0012 0.0587
1.732 11.63 -0.1103-0.0128-0.1022-0.0119-0.1029-0.0119 0.0007 0.0437
1.414 9.47 -0.0734-0.0070-0.0656-0.0062-0.0657-0.0062 0.0001 0.0289
1.000 6.68 -0.0367-0.0024-0.0291-0.0020-0.0287-0.0019-0.0004 0.0143
0.000 0.00 -0.0000 0.0000 0.0072 0.0000 0.0082 0.0000-0.0009
Аберрации главного луча: астигматизм,дисторсия и сф.аберрация в зрачках
Предм. 100tg W'= Y' == dY'== dY'12 = Z'm == Z's =Z'm-Z's= Sp === Sp' =
22~21' 55.52 6.5683 0.4009 0.0120-5.1243-2.1357-2.9886 9.170-2.6565
15~48' 36.14 4.3537 0.1086 0.0156-2.5141-1.0550-1.4591 9.170-2.8752
Аберрации широких наклонных пучков
Зона предмета: 1.000 Меридиональное сечение
========= M d100tgб' dY(Л0) dY(Л1) dY(Л2) =Кома==================
1.000 2.000 25.676 -1.4966-1.5051-1.4831 -0.4313
0.866 1.732 21.553 -1.2139-1.2192-1.2040-0.3176
0.707 1.414 17.003 -0.9191-0.9211-0.9129-0.2079
0.500 1.000 11.544 -0.5911-0.5897-0.5889-0.1022
0.000 0.000 -0.000 0.0000 0.0072-0.0048
-0.500 -1.000 -9.910 0.3867 0.3974 0.3775
-0.707 -1.414-13.670 0.5033 0.5148 0.4927
-0.866 -1.732-16.450 0.5788 0.5909 0.5673
-1.000 -2.000-18.728 0.6340 0.6465 0.6219
Важно отметить, что значение комы берем с виньетированного пучка (для этого в RAYS надо написать не D’ [диаметр выходного зрачка, обычно в пределах 4-5 мм], а половину D, тогда пучок будет усечен на 50 % и она будет виньетирован).
Формулы для расчета аберраций I и III порядка для ППП:
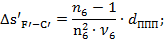
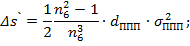
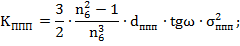
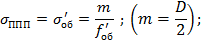
Исправление хроматизма положения для объектива и ППП:
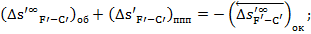
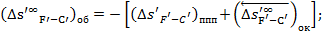
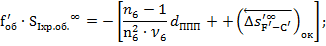
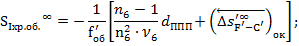
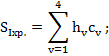
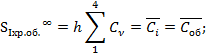
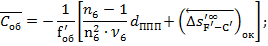
Исправление сферической аберрации III-го порядка:
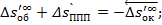
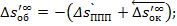
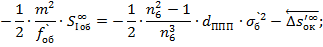
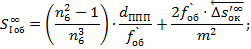
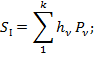
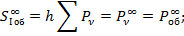
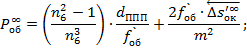
Исправление меридиональной комы 3-го порядка:
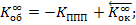
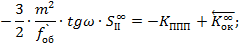
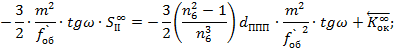
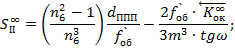
С учётом нормировки начальных координат:
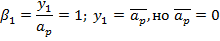
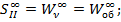
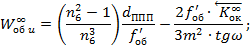
Полученные формулы:
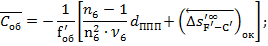
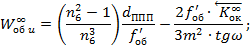
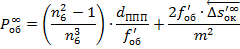
Важное примечание!
Если дело касается бинокля с оборачивающей системой Малафеева-Порро 1-го рода, то в формулы к члену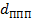 
добавится двойка, так как призм в этой оборачивающей системе две!
