Задача 10
Найти: 1) длину стороны АВ; 2) уравнение стороны АВ; 3) уравнение высоты CD и его длину; 4) уравнение окружности, для которой высота CD является диаметром.
А (-2;2) B (10;-7) С (8;7)
Решение:

Длина стороны АВ.
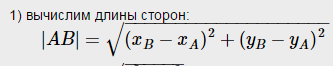
АВ=√(2-(-7))²+(10-(-2))² = √(81+144)=√225= 15
Уравнения стороны АВ.
Уравнение прямой Y=kX+b.
Уравнение прямой АВ
k =dY/dX = - 9/12 = -3/4
b = Ay - k*Ax = 2 -(-3/4)*(-2) = 0.5
Окончательно уравнение прямой Y(AB) = -3/4*X + 0.5
4.Уравнение высоты CD и её длину.
Высота CD - перпендикуляр к прямой АВ и наклон по формуле
k = - 1/k(AB) = - 1 /(-3/4) = 4/3.
Сдвиг В по точке С(8;7).
b = Cy - k*Cx = 7 - 4/3*8 = - 3, 2/3
Окончательно уравнение высоты CD - Y(CD) = 4/3*X – 3, 2/3
Дополнительно находим точку пересечения D решая систему уравнений из параметрических уравнений прямых AB и CD.
4*Y+3*X = 2 - уравнение AB
3*Y - 4*X = -11 - уравнение СD.
Решаем быстро методом Крамера - det D = -25, detY= 25, detX= 50.
Dx = 2 Dy= - 1.
Длина высоты CD - по теореме Пифагора.
CD = √(8² + 6²)= √100 = 10 - длина высоты - диаметр окружности -
5. Уравнение окружности с центром O на высоте CD.
Центр окружности - середина отрезка AD -
Ox = (Cx+Dx)/2 = (8+2)/2 = 5
Oy = *Cy+Dy)/2) = (7+(-1))/2 = 3.
Уравнение окружности со смещенным центром в т. О(5;3) и радиусом R=5.
(x-5)² + (y-3)² = 25
Задача 20
Найти производную данной функции:
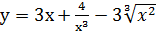 ;
;
Решение:

Задача 30
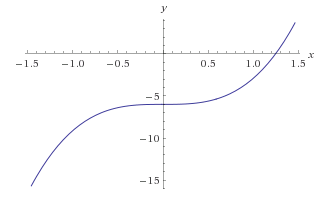
Исследовать функцию методами дифференциального исчисления и построить их графики. При исследовании функции нужно найти интервалы возрастания и убывания и точки экстремума функции, интервалы выпуклости и вогнутости и точки перегиба графика функции.

Решение:
1. Находим интервалы возрастания и убывания. Первая производная.

Решение ищем по формуле:
(xn)' = n xn-1

(x)' = 1
Ответ:


Находим нули функции. Для этого приравниваем производную к нулю
75 • x2 = 0
Откуда:x1 = 0
| (-∞;0) | (0; +∞) |
| f'(x) > 0 | f'(x) > 0 |
| функция возрастает | функция возрастает |
3. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

Откуда точки перегиба:x1 = 0
| (-∞;0) | (0; +∞) |
| f''(x) < 0 | f''(x) > 0 |
| функция выпукла | функция вогнута |
Задача 40
Вычислить указанные неопределенные интегралы:

Решение:

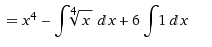
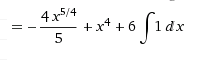
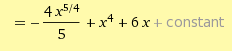
Задача 50
Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной указанными линиями. Сделать чертеж
у = sinx , х=0, х=  , у=0.
, у=0.
Решение
Объем тела вращения, образованного вращением графика y=f(x) вокруг оси Ox, может быть вычислен по формуле

a=0, b=  , f(x)=sinx, подставляем в формулу, получаем
, f(x)=sinx, подставляем в формулу, получаем


Задача 60
Найти частное решение дифференциального уравнения, удовлетворяющее указанному начальному условию
 , у(0) = 1.
, у(0) = 1.
Решение
y'-y=exp(2*x)
Представим в виде:
-y+y' = e2 • x
Это неоднородное уравнение. Рассмотрим соответствующее однородное уравнение:
-y+y'= 0
1. Решая его, получаем:
y' = y

Интегрируя, получаем:
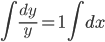
ln(y) = x
y = ex
Ищем теперь решение исходного уравнения в виде:
y(x) = C(x)(ex), y'(x) = C(x)'(ex) + C(x)(ex)'
C(x) • ex+C(x)' • ex-y=e2 • x
C(x)' • ex = e2 • x
или
C(x)' = ex
Интегрируя, получаем:

Из условия y(x)=C(x)•y, получаем:
y(x) = C(x)•y = (C+ex) • ex
или
y = C • ex+e2 • x
Найдем частное решение при условии: y(0) = 1
y(0) = C+1 = 1
Откуда:
c1 = 0
Таким образом, частное решение имеет вид:
y(0) = e2 • x
Задача 70 
Найти общее решение дифференциальных уравнений второго порядка.

Решение:
Вычислим корни характеристического уравнения:
x=(-b±√D)/2a, D=b²-4ac
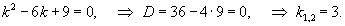
Как видно, характеристическое уравнение имеет один корень второго порядка: k1 = 3.
Поэтому общее решение дифференциального уравнения определяется формулой
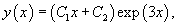
где C1, C2 − произвольные действительные числа.
Задача 80
Бросаются две игральные кости. Найти вероятность того, что суммам выпавших очков равна восьми
Решение:
2 броска, значит, количество возможных вариантов равно 6*6=36.
Чтобы получилось в сумме 8 при 2 бросках, должны выпасть следующие комбинации в первом и втором броске.
4+4 =8;
3+5 =8;
5+3=8;
2+6 =8;
6+2 =8.
Благоприятных вариантов, (которые дают в сумме 8 очков), всего 5. А всего возможных вариантов события 36. Отношение количества благоприятных исходов к общему числу исходов 5/36=0,138888888. В ответе запишем 0, 139 (округлили до тысячных)
Задача 90
Вычислить выборочный коэффициент корреляции двух случайных величин X и Y и найти выборочное уравнение прямой регрессии Y на X.
| x | ||||||||||
| y |
Решение:
| Rx,y | = |
| , (1.4) где: |
| Mx | = |
|
| xk, | My | = |
|
| yk, | Mxy | = |
|
| (1,5)xkyk |
| Sx2 | = |
|
| xk2 - Mx2, | Sy2 | = |
|
| yk2 - My2 (1,6) |
Вычислим коэффициент корреляции по формуле (1.4), для этого вычислим значения xk2, yk2 и xkyk и занесем их в таблицу 1.
Таблица 1
| k | xk | yk | хk 2 | yk 2 | хkyk |
| 484.00000 | 625.00000 | 550.00000 | |||
| 529.00000 | 900.00000 | 690.00000 | |||
| 576.00000 | 900.00000 | 720.00000 | |||
| 625.00000 | 900.00000 | 750.00000 | |||
| 625.00000 | 1225.00000 | 875.00000 | |||
| 529.00000 | 625.00000 | 575.00000 | |||
| 324.00000 | 625.00000 | 450.00000 | |||
| 441.00000 | 400.00000 | 420.00000 | |||
| 361.00000 | 100.00000 | 190.00000 | |||
| 400.00000 | 100.00000 | 200.00000 |
Вычислим Mx по формуле
Сложим последовательно все элементы xk
x1 + x2 + … + x10 = 22.00000 + 23.00000 +... + 20.00000 = 220.000000
Разделим полученную сумму на число элементов
220.00000 / 10 = 22.00000
Mx = 22.000000
Аналогичным образом вычислим My.
Сложим последовательно все элементы yk
y1 + y2 + … + y10 = 25.00000 + 30.00000 +... + 10.00000 = 240.000000
Разделим полученную сумму на число элементов выборки
240.00000 / 10 = 24.00000
My = 24.000000
Аналогичным образом вычислим Mxy.
Сложим последовательно все элементы 6-го столбца таблицы 1
550.00000 + 690.00000 +... + 200.00000 = 5420.000000
Разделим полученную сумму на число элементов
5420.00000 / 10 = 542.00000
Mxy = 542.000000
Вычислим значение Sx2
Сложим последовательно все элементы 4-го столбца таблицы 1
484.00000 + 529.00000 +... + 400.00000 = 4894.000000
Разделим полученную сумму на число элементов
4894.00000 / 10 = 489.40000
Вычтем из последнего числа квадрат величины Mx получим значение для Sx2
Sx2 = 489.40000 - 22.000002 = 489.40000 -484.00000 = 5.40000
Вычислим значение Sy2
Сложим последовательно все элементы 5-го столбца таблицы 1
625.00000 + 900.00000 +... + 100.00000 = 6400.000000
Разделим полученную сумму на число элементов
6400.00000 / 10 = 640.00000
Вычтем из последнего числа квадрат величины My получим значение для Sy2
Sy2 = 640.00000 - 24.000002 = 640.00000 -576.00000 = 64.00000
Вычислим произведение величин Sx2 и Sy2.
Sx2Sy2 = 5.40000 • 64.00000 = 345.600000
Извлечем и последнего числа квадратный корень, получим значение SxSy.
SxSy = 18.59032
Вычислим значение коэффициента корреляции
R = (542.00000 - 22.00000 • 24.00000) / 18.59032 = (542.00000 –
528.00000) / 18.59032 = 0.75308
ОТВЕТ: Rx,y = 0.753080
4. Вычисляем коэффициенты уравнения регрессии.
Уравнение линейной регрессии представляет собой уравнение прямой, аппроксимирующей (приблизительно описывающей) зависимость между случайными величинами X и Y. Если считать, что величина X свободная, а Y зависимая от Х, то уравнение регрессии запишется следующим образом
Y = a + b•X (2.1), где:
| b = | Rx,y |
| = | Rx,y |
|
a = My - b•Mx
Рассчитанный коэффициент b называют коэффициентом линейной регрессии. В некоторых источниках a называют постоянным коэффициентом регрессии и b соответственно переменным.
Погрешности предсказания Y по заданному значению X вычисляются по формулам:
| σy/x = σy |
| = Sy |
| - абсолютная погрешность, |
| δy/x = |
| 100% - относительная погрешность |
Величину σy/x еще называют остаточным средним квадратическим отклонением, оно характеризует уход величины Y от линии регрессии, описываемой уравнением при фиксированном (заданном) значении X.
| Вычислим отношение |
| . |
Sy2 / Sx2 = 64.00000 / 5.40000 = 11.85185
| Вычислим отношение |
| . |
Извлечем из последнего числа квадратный корень - получим:
Sy / Sx = 3.44265
Вычислим коэффициент b
b = 0.75308 • 3.44265 = 2.59259
Вычислим коэффициент a
a = 24.00000 - 2.59259 • 22.00000 = -33.03704
Оценим погрешности уравнения регрессии.
Извлечем из Sy2 квадратный корень получим:
| Sy = |
| = 8.00000; | ||||
Возведем в квадрат Rx,y получим:
R2x,y = 0.753082 = 0.56713
Вычислим абсолютную погрешность (остаточное среднее квадратическое отклонение)
| σy/x = 8.00000 |
| = 5.26343 |
Вычислим относительную погрешность
δy/x = (5.26343 / 24.00000)100% = 21.93096%
| ОТВЕТ: | Уравнение линейной регрессии имеет вид: Y = 2.59259 X -33.03704 (2.6) |
| Погрешности уравнения: σy/x = 5.26343; δy/x = 21.93096% |






