I. Цели и задачи занятия
1. Выработать навыки исследования функций на монотонность и экстремумы с помощью первой производной.
2. Показать обучающимся важность данной темы в курсе изучаемой дисциплины.
3. Воспитывать у обучающихся настойчивость в достижении поставленной цели.
II. План проведения и расчет учебного времени
| Содержание и порядок проведения занятия | Время, мин |
| ВВОДНАЯ ЧАСТЬ | |
| ОСНОВНАЯ ЧАСТЬ Учебные вопросы: | |
| 1. Монотонность и экстремумы. | |
| 2. Исследование функций. | |
| ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ | |
| ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ |
III. Учебно-материальное обеспечение
Классная доска, раздаточный материал, планшет, видеопроектор, экран.
IV. Методические материалы
К проведению практического занятия
Во вводной части занятия (5 мин.) после объявления темы и целей практического занятия целесообразно изложить последовательность обсуждения учебных вопросов.
Первый учебный вопрос (10 мин).
Монотонность и экстремумы.
При изложении первого учебного вопроса следует напомнить обучающимся понятие монотонной функции, необходимое и достаточное условия существования экстремума в точке.
Функция  называется возрастающей в некотором интервале, если большему значению аргумента соответствует большее значение функции, т.е. если
называется возрастающей в некотором интервале, если большему значению аргумента соответствует большее значение функции, т.е. если  =>
=>  (если
(если  =>
=> 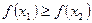 – неубывающая).
– неубывающая).
Функция  называется убывающей в некотором интервале, если большему значению аргумента соответствует меньшее значение функции, т.е. если
называется убывающей в некотором интервале, если большему значению аргумента соответствует меньшее значение функции, т.е. если  =>
=>  (если
(если  =>
=>  – невозрастающая).
– невозрастающая).
Возрастающие и убывающие функции называются монотонными (строго монотонными). Интервалы, в которых функция монотонна, называются интервалами монотонности.
Признаки монотонности: Если дифференцируемая на интервале 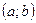 функция
функция  возрастает (убывает), то
возрастает (убывает), то  (
( ) для
) для  .
.
Геометрическое утверждение означает, что касательные к графику возрастающей функции образуют острые углы с  (т.к.
(т.к.  =>
=>  – острый).
– острый).
Точками экстремума функции являются точки максимума и минимума.
Необходимое условие экстремума: Если дифференцируемая функция  имеет экстремум в точке
имеет экстремум в точке  , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю:  .
.
Достаточные условия возрастания и убывания функции: Если функция  дифференцируема на интервале
дифференцируема на интервале 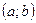 и
и 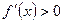 (
( ) для
) для  , то эта функция возрастает (убывает) на интервале
, то эта функция возрастает (убывает) на интервале 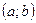 .
.
Точки, в которых производная равна нулю или не существует, называются критическими точками (т.е. подозрительными на экстремум, в них возможен экстремум, но может и не быть).
Первое достаточное условие существование экстремума: Если непрерывная функция  дифференцируема в некоторой окрестности критической точки
дифференцируема в некоторой окрестности критической точки  и при переходе через нее (слева направо) производная
и при переходе через нее (слева направо) производная  меняет знак с «+» на «–», то
меняет знак с «+» на «–», то  – точка максимума, с «–» на «+», то
– точка максимума, с «–» на «+», то  – точка минимума (если знак не меняется – экстремума нет).
– точка минимума (если знак не меняется – экстремума нет).
Схема исследования функции на монотонность и экстремумы:
1. Найти производную функции  .
.
2. Найти все критические точки из области определения функции, для этого:
а)  – найти корни, которые являются внутренними точками области определения;
– найти корни, которые являются внутренними точками области определения;
б) найти значения аргумента, при которых производная не существует.
3. Установить знаки производной функции при переходе через критические точки и выписать точки экстремума.
4. Вычислить значения функции в точках экстремума.
Второе достаточное условие существование экстремума: Если в точке  первая производная функции
первая производная функции  равна нулю (
равна нулю ( ), а вторая производная в точке
), а вторая производная в точке  существует и отлична от нуля (
существует и отлична от нуля ( ), то при
), то при  в точке
в точке  функция имеет максимум и минимум – при
функция имеет максимум и минимум – при  .
.
Правило исследования функции на экстремум с помощью второй производной:
1. Найти первую производную  .
.
2 Приравняв ее к нулю, найти критические точки.
3. Найти вторую производную  .
.
4. Найти значения  в критических точках:
в критических точках:
если она окажется <0, то критическая точка – точка максимума;
если она окажется >0, то критическая точка – точка минимума.
Вопросы, задаваемые обучающимся:
- Какая функция называется возрастающей (неубывающей)?
- Какая функция называется убывающей (невозрастающей)?
- Что такое интервалы монотонности функции?




