Пользуясь данными таблицы 2.1, необходимо определить коэффициенты проницаемости для зоны 1 (L4 + L5 + L6) и зоны 2 (L1 + L2 + L3) по формуле
 (2.9)
(2.9)
где
k - коэффициент проницаемости отдельной секции модели пласта,мкм2;
μ - динамическая вязкость воды, Па·с;
ΔР - перепад давления между концами секций модели пласта, Па;
F - площадь сечения трубы с пористой средой, 28,26·10-4, м2 (d = 0,06 м).
Q - расход жидкости, m3/c.
| Номер режима | V,M3 | t,c | Q, м3/с | Pк, Па | Рс, Па | (Рк-Рс), Па | Кт, м3/(Па·с) |
Здесь ρн = 1 000 кг/м3.
По данным таблицы 3.2 следует построить индикаторные диаграммы скважины, как показано на рисунках 3.5 и 3.6.
По графику на рисунке 3.5 при Q = 0 следует определить значение давления на контуре питания Рк и сопоставить с фактическим его значением по пьезометру П1.
По индикаторной диаграмме (рисунок 3.6) определяется коэффициент продуктивности скважин.


Рисунок 3.5 Рисунок 3.6
Примеры построения индикаторных диаграмм скважины
Коэффициентом продуктивности добывающей скважины называется прирост (снижение) дебита жидкости при увеличении (снижении) депрессии на пласт на единицу, т.е.
 =
=  (3.14)
(3.14)
Вопросы для самоподготовки
1. Какие различают типы неоднородности пластов?
2. Какие причины приводят к неоднородности строения пластов?
3.Каковы особенности фильтрации жидкостей в неоднородных пластах?
4.Рассказать об основных элементах экспериментальной установки, предназначенной для изучения фильтрации жидкости в неоднородном пласте.
5.Как распределяется давление и градиент давления в пласте, проницаемость которого изменяется скачкообразно?
6.Какие задачи решаются в лабораторной работе?
7.Какие существуют соотношения между градиентом давления и коэффициентом проницаемости при зональной неоднородности пласта?
8.Как рассчитываются средние значения проницаемости пласта по значениям коэффициентов проницаемости отдельных зон?
Список использованных источников
1) Басниев К.С. Подземная гидравлика /К.С. Басниев, А.М. Власов, И.Н. Кочина.М.: Недра.1986. - С. 69-78.
2) Пыхачев Г.В. Подземная гидравлика /Г.В. Пыхачев, Р.Г. Исаев. - М.: Недра, 1973.-С. 94-100.
Рисунок 3.4 - Распределение давления по радиусу кругового пласта
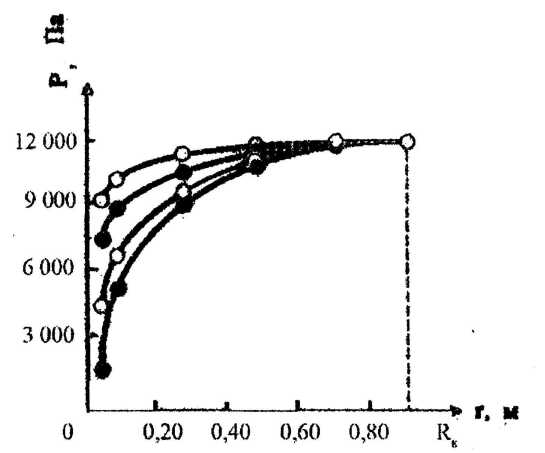
| По результатам расчётов необходимо построить график распределения давления в залежи круговой формы в координатах "Р-r" как показано на рисунке 3.4. Графики выполняются в масштабах, рассчитанных на всю страницу. |

Дифференциальное уравнение установившейся фильтрации для случая плоскофильтрационного потока (уравнение Лапласа) имеет вид:
 = 0 (3.1)
= 0 (3.1)
Если уравнение Лапласа представить в цилиндрических координатах, то для плоскорадиального потока, вследствие осевой симметрии, характеристики потока не зависят от угла j, а являются функциями только координаты r, и уравнение имеет вид:
За начало отсчета уровней в пьезометрах принято положение статического уровня. Поэтому фактическое значение динамического уровня жидкости от устья "скважин-пьезометров" рассчитывается по формуле
hд = h ст + h1 д (3.10)
где
h1 д - расстояние до динамического уровня жидкости в скважинах-пьезометрах, м.
Переход от динамических уровней к высоте столба жидкости в скважинах-пьезометрах производится по формуле
 (3.11)
(3.11)
а к давлению - по формуле
 (3.12)
(3.12)
где
Н - высота столба воды в скважине-пьезометре, м;
ρ- плотность воды (1000 кг/м3);
g - ускорение силы тяжести (9,81 м/с2).
Градиент давления вдоль радиуса r залежи круговой формы меняется по следующей зависимости:
 =
=  (3.6)
(3.6)
Скорость фильтрации жидкости в любой точке залежи на радиусе г от скважины можно определить по формуле
 (3.7)
(3.7)
где
к - коэффициент проницаемости пласта;
μ - динамическая вязкость фильтрующейся жидкости.
Градиент давления и скорость фильтрации носят гиперболический характер, причем при приближении к скважине их величины резко возрастают. Дебит определяется по формуле Дюпюи:
 (3.8)
(3.8)
где h - толщина пласта.
Важной характерной особенностью формулы Дюпюи является слабая зависимость дебита Q от радиуса Rк контура питания для достаточно больших значений Rk/rс как радиусы Rk и rс входят в нее под знаком логарифма.
Исследование особенностей плоскорадиальной фильтрации имеет весьма большое значение для понимания законов притока жидкости или газа к скважинам. В случае гидродинамической совершенной скважины плоскорадиальным потоком следует считать тот, который возникает в призабойной зоне пласта, т.е. в ближайшей к скважине зоне пласта.




