, 
. (4)
Для определения их вида необходимо найти корни характеристического уравнения
, (5)
где 1 – единичная матрица. В результате получаем
. (6)
Корни характеристического уравнения
, (7)
где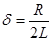 
- показатель затухания, (8)
- резонансная частота LС контура. (9)
Корни характеристического уравнения позволяют оценить продолжительность переходного процесса. Временем переходного процесса обычно считают промежуток, в течение которого свободная составляющая уменьшается в 
… 
раз. Для оценки длительности или скорости протекания переходного процесса вводится понятие постоянной времени 
, (10)
за это время свободная составляющая тока или напряжения контура уменьшается в 
раз. С помощью постоянной времени можно оценить длительность переходного процесса:
. (11)
Характер свободного процесса зависит от вида корней 
, которые зависят от параметров цепи и может быть:
1) Апериодическим при отрицательных вещественных разных корнях, если 
, корни определяются по формуле (7).
В этом случае напряжение монотонно уменьшается, ток, возрастая по модулю от нуля, достигает максимума, а затем также уменьшается (рис. 12.2), перезарядки конденсатора не происходит. В этом случае общее решение системы дифференциальных уравнений имеет вид:
, (12)
, (13)
где 
, 
, 
, 
- постоянные интегрирования, определяемые из начальных условий (законов коммутации).
Постоянная времени апериодического переходного процесса приближенно может быть оценена по формуле:
.
При расчете постоянных интегрирования используют независимые начальные условия. К независимым начальным условиям относятся напряжение на конденсаторе и ток через катушку. По законам коммутации эти величины сохраняют свои значения в момент коммутации.
Для расчета двух постоянных интегрирования , необходимо два уравнения, в которых присутствуют значение функции и ее производной в момент коммутации. Например, для апериодического колебательного процесса:
, 
. (14)
При 
получаем
, 
. (15)
Учитывая начальные условия, что 
(рис. 12.4), а 
, получаем
и 
. (16)
2) Колебательным при комплексно сопряженных с отрицательной вещественной частью корнях, если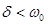 
, корни характеристического уравнения можно записать в виде:
, (17)
где 
- мнимая единица, а 
- угловая частота свободных (собственных) затухающих колебаний контура:
. (18)
В этом случае напряжение и ток элементов цепи изменяются по закону затухающей синусоиды, а реактивные элементы цепи многократно обмениваются энергией между собой. Решение уравнений цепи удобно записать в виде:
,
, (19)
где 
- аргумент комплексного корня, 
, 
; (20)
, 
. (21)
Период свободных колебаний контура равен 
. (22)
Постоянная времени колебательного переходного процесса может быть определена по формуле:
.
Кривые напряжения и тока (рис. 12.3) представляют затухающие синусоидальные колебания, их амплитуды уменьшаются по экспоненциальному закону 
. Быстроту затухания характеризуют декрементом затухания 
, который определяется как отношение двух значений напряжения (или тока), отстоящих друг от друга на один период свободных колебаний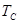 
:
; (23)
3) Критическим при отрицательными вещественных равных корнях, если 
. Это соответствует предельному случаю апериодического процесса и активное сопротивление цепи
- называется критическим, а (24)
- характеристическим сопротивлением контура. (25)
Решение уравнений цепи имеет вид
,
. (26)
Ток достигает максимума 
в момент времени 
. (27)
Такой переходной процесс имеет самую малую продолжительность для данных параметров реактивных элементов.
Зависимости токов и напряжений показаны на рис. 12.2 для апериодического и на рис. 12.3 для колебательного переходного процесса.
Рис. 12.2. Зависимости токов и напряжений для апериодического переходного процесса.
|
Рис. 12.3. Зависимости токов и напряжений для колебательного переходного процесса
|
Некоторые параметры переходного процесса можно определить по снятой экспериментально временной диаграмме.
Для определения постоянной времени 
апериодического переходного процесса достаточно построить касательную к любой точке диаграммы. Постоянная времени будет численно равна отрезку времени от точки касания до пересечения касательной с осью времени (рис. 12.4).
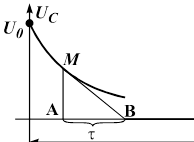
Рис. 12.4. Определение постоянной времени.
Период свободных колебаний 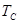при колебательном переходном процессе может быть определен непосредственно по временной диаграмме (рис. 12.5).
Декремент затухания свободных колебаний при колебательном переходном процессе можно определить как отношение амплитуд двух соседних периодов (рис. 12.5):
. (27)
Рис. 12.5. Определение периода и декремента затухания колебаний.
Содержание и порядок выполнения работы
Процесс разряда конденсатора С на цепь RL в лабораторной работе исследуют в цепи по схеме, приведенной на рис. 12.6.
Рис. 12.6. Функциональная схема цепи.
В лабораторной работе используют модули ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР, НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ. Для наблюдения зависимостей от времени используют ОСЦИЛЛОГРАФ. Пассивные элементы электрической схемы выбирают из блоков МОДУЛЬ РЕАКТИВНЫХ ЭЛЕМЕНТОВ и МОДУЛЬ РЕЗИСТОРОВ. Рекомендуемые параметры элементов приведены в таблице 12.1.
Таблица 12.1
| Вариант | ||||||||||
 ,мГн
| ||||||||||
 ,мкФ
| 6.8 | 6.8 | 6.8 | 6.8 | 6.8 | 6.8 |
Активное сопротивление R к катушки измеряют МУЛЬТИМЕТРОМ.
Конденсатор С в интервале времени от 0 до Т /2 заряжается через диод VD1 модуля НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ и катушку до напряжения 
с выхода модуля ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР. В момент времени t = Т /2 напряжение на выходе модуля становится равным 
и диод VD1 закрывается. Емкость С разряжается на цепь R 1- R к- L (рис. 12.7). Далее процесс повторяется, что дает возможность наблюдать временные зависимости на экране осциллографа.
Рис. 12.7. Осциллограмма напряжения на конденсаторе.
Подготовительный этап.
• Собрать электрическую цепь по схеме, показанной на рис. 1П. Конденсатор С и индуктивность L взять из блоков МОДУЛЬ РЕАКТИВНЫХ ЭЛЕМЕНТОВ, резистор R 1, – из блока МОДУЛЬ РЕЗИСТОРОВ, диод VD1 – из блока НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ.
• Установить в модуле РЕАКТИВНЫЕ ЭЛЕМЕНТЫ заданные преподавателем значения. Записать значения в протокол измерений.
• Измерить мультиметром активное сопротивление R к катушки. При измерении следует отключить катушку от собранной цепи и подключить отдельными проводами к мультиметру. Записать результат в протокол измерений.
• Проверить собранную электрическую цепь в присутствии преподавателя.
Без проверки преподавателем включать цепь категорически запрещается.
• Включить автоматический выключатель QF блока МОДУЛЬ ПИТАНИЯ и тумблер Сеть модуля ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР. Переключатель Форма включить в положение 
. Регулятором Частота установить на выходе модуля ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР частоту f = 40-50 Гц. Регулятором Амплитуда установить амплитуду (совпадает с действующим значением для сигнала прямоугольной формы) напряжения U = 4-5 В. Значение U записать в протокол измерений.
• Включить ОСЦИЛЛОГРАФ. Настроить нулевое значение сигнала, повернуть ручки регулятора вертикальной развертки («усиление плавно») и регулятора горизонтальной развертки («развертка плавно») до упора по ходу часовой стрелки.
• Подключить Вход 1 осциллографа к источнику. Настроить ручки горизонтальной развертки осциллографа таким образом, чтобы на экране полностью укладывался один период колебаний. Настроить переключатель усиления по напряжению так, чтобы максимально использовалась площадь экрана. Используя масштаб 
на переключателе усиления по напряжению убедиться, что амплитуда входного напряжения 
В.
В остальных опытах использовать указанный порядок настройки осциллографа.
Апериодический разряд емкости С на цепь R-L
• Установить значение сопротивления R 1 = 100 Ом в блоке МОДУЛЬ РЕЗИСТОРОВ. Рассчитать в протоколе измерений величину сопротивления R кр.
Убедиться, что R 1 + R к > R кр.
• Подключить Вход 1 осциллографа к конденсатору С. Срисовать на кальку с экрана ОСЦИЛЛОГРАФА кривую зависимости 
. На рисунке написать масштабы , 
.
• Подключить Вход 1 осциллографа к резистору R 1. Срисовать на кальку с экрана ОСЦИЛЛОГРАФА кривую зависимости 
. На рисунке написать масштабы , .
