Свободное движение жидкости (свободная конвекция) происходит под влиянием разности плотностей нагретых и холодных частиц. Эта разность плотностей зависит от разности температур твердого тела и жидкости. Форма твердого тела имеет второстепенное значение, и поэтому уравнение подобия теплоотдачи имеет вид:
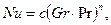(1)
где с и n- константы, численные значения которых зависят от режима движения жидкости, т.е. от произведения GrPr:
| Режим | с | n |
Ламинарный (GrPr  )
| 1,18 | 0,125 |
Пререходный (GrPr  )
| 0,54 | 0,25 |
Турбулентный (GrPr  )
| 0,135 | 0,33 |
В качестве определяющих геометрических размеров при вычислении числа Грасгофа в формуле (1) приняты: для цилиндрических или сферических тел- диаметр, для плоских плит- их высота. В качестве определяющей температуры, т.е. температуры, по которой определяются значения физических параметров, входящих в числа подобия, здесь принята средняя температура пограничного слоя 
, где 
- температура стенки и 
- температура жидкости в ядре. Значение разности температур в числе Грасгофа 
.
Теплоотдача при вынужденном движении жидкостей. Интенсивность теплоотдачи при вынужденном движении жидкостей зависит в первую очередь от характера движения. Соответственно этому в дальнейшем рассматриваются теплоотдача в условиях установившегося турбулентного движения, теплоотдача в условиях ламинарного движения и теплоотдача в условиях неустойчивого турбулентного движения.
В условиях установившегося турбулентного движения (Re>10000) теплоотдача зависит практически только от характера движения и свойств жидкости; наиболее точные результаты для этого случая теплоотдачи дает зависимость
. (2)
Физические параметры в числах Nu, Re и Pr определены при средней температуре жидкости, а в числе 
при температуре стенки. Отношение 
в степени 0,25 учитывается влияние на теплоотдачу направления теплового потока и температурного перепада. Определяющим геометрическим размером принят эквивалентный диаметр канала, равный учетверенной площади поперечного сечения канала, деленной на смоченный периметр. Зависимость (2) справедлива для случаев движения жидкости по прямым каналам любой формы поперечного сечения.
В коротких каналах и трубах коэффициент теплоотдачи больше, чем в длинных. Практически он заметно уменьшается с увеличением отношения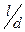 
от 1 до 50. Дальнейшее увеличения 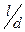не приводит к уменьшению коэффициента теплоотдачи. Если отношение 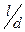меньше чем 50, в равенство (2) вводится поправочный коэффициент 
, численные значения которого приведены в табл.1.
При движении жидкости по изогнутой трубе или каналу теплообмен интенсивнее, чем при движении по прямому каналу. Увеличение интенсивности теплообмена в этом случае учитывается поправочным коэффициентом, который вводится в формулу (2): 
, (3)
где диметр трубы или канала; R- радиус кривизны трубы или канала.
Соотношение (2) справедливо для труб и каналов, имеющих гладкие стенки. Для шероховатых стенок увеличивается коэффициент теплоотдачи, однако это обстоятельство обычно не учитывается в практических расчетах.
В условиях ламинарного движения (Re≤2300) теплоотдача определяется как вынужденным, так и свободным движением жидкости. Для расчета теплоотдачи при ламинарном движении наиболее точной является формула
. (4)
Эта формула справедлива при 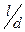>50. В качестве определяющего размера принят эквивалентный диаметр канала. Физические параметры в числах Nu, Re, Рг и Gr определены при средней температуре жидкости, а в числе при температуре стенки.
В условиях неустойчивого турбулентного движения, т.е. переходном режиме (2З00<Re<10000), теплоотдача может быть рассчитана с помощью функции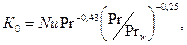 
значения которой для различных чисел Rе приведены ниже:
| 2,3 | 2,5 | 3,0 | 3,5 | 4,0 | ||||||
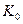
| 3,6 | 4,9 | 7,5 | 12,2 | 16,5 |
В условиях вынужденного поперечного потока жидкости теплоотдача от стенки одиночной трубы определяется режимом движения я может быть рассчитана по следующим формулам: при 
(5)
При 
(6)
При вынужденном потоке жидкости теплоотдача пучка труб имеет ту особенность, что интенсивность теплообмена во втором и третьем по ходу газа рядах пучка возрастает по сравнению с интенсивностью в первом ряду. Этот рост интенсивности обусловливается турбулизацией потока при прохождении через пучок труб. Начиная с третьего ряда турбулизация стабилизируется и вместе с этим стабилизируется теплоотдача. Для третьего и последующих рядов пучка труб (при ) теплоотдача может быть рассчитана при шахматном расположении труб по формуле (7), а при коридорном по (8):
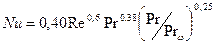(7)
(8)
Коэффициент теплоотдачи для первого ряда пучка труб принимают равным 60%, для второго ряда при шахматном расположении 7О%, а при коридорном 90% от значения, найденного по формуле соответственно (7) и (8) для третьего ряда.
В формулах (4), (5), (6) в качестве определяющего размера принят диаметр трубы. Физические параметры в числах Nu, Rе и Рг определены при средней температуре жидкости, а в числе при температуре стенки. В качестве определяющей скорости принята скорость в самом узком сечении ряда.
