РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ ЭЛЕКТРОННОЙ ТАБЛИЦЫ EXCEL
Для решения нашей задачи в ячейку E1 вводится значение расхода входного потока G01.
В ячейки E5, E6 задаются начальные значения для поисковых переменных
G34, G12.
В ячейках E11-E18 осуществляется расчет ХТС в соответствии с установленной последовательностью.
В ячейках F21,F22 вычисляются рассогласования по расходам в местах разрыва потоков в виде квадратов разностей.
В ячейку E26 заносится суммарное рассогласование по расходу разорванных потоков. Далее с помощью поиска решения минимизируем квадрат суммы по G34 и G12. Результаты решения представлены на рисунке- 4.4.
Рисунок 4.4 - Результаты решения задачи декомпозиционного расчета ХТС
с помощью EXCEL
4.3.2 РЕШЕНИЕ ЗАДАЧИ В MATHCAD МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ С ПОМОЩЬЮ
ЭЛЕМЕНТОВ ПРОГРАММИРОВАНИЯ
Рисунок 4.5 - Результаты решения задачи декомпозиционного расчета ХТС с помощью MATHCAD
4 .3.3 РЕШЕНИЕ ЗАДАЧИ В MATHCAD МЕТОДОМ ВЕГСТЕЙНА
С ПОМОЩЬЮ ЭЛЕМЕНТОВ ПРОГРАММИРОВАНИЯ
Рисунок 4.6-Протокол решения задачи (начало)
Рисунок 4.7- Протокол решения задачи (окончание)
РЕШЕНИЕ ЗАДАЧИ В MATHCAD С ПОМОЩЬЮ ПРОЦЕДУРЫ МИНИМИЗАЦИИ
Рисунок 4.8 - Результат решения задачи
Ниже представлены результаты декомпозиционного расчета ХТС с использованием метода простой итерации
| Исходные данные | Рассчитанные значения расходов потоков | ||||||||||
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| k |
| 123,4 | 370,2 | 740,4 | 176,5 | 264,7 | 434,8 |
4.4 ИНТЕГРАЛЬНЫЙ МЕТОД РАСЧЕТА
Интегральный метод расчета предполагает совместное решение уравнений математического описания элементов ХТС.
Для рассматриваемого примера эти уравнения имеют вид:
1-й элемент 
,
2-й элемент 
3-й элемент 
4-й элемент 
Неизвестные: 
определяются из решения системы из 8-и уравнений с 8-ю неизвестными. Для данной ХТС эта система уравнений линейная.
Введем следующие обозначения:
|
| 
| 
| 
| 
| 
| 
| 
|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 |
Результат решения задачи представлен на рисунке 4.9.
Рисунок 4.9 - Результат решения задачи интегральным методом
РАЗДЕЛ 2
КОНТРОЛЬНЫЕ ЗАДАНИЯ.
Номера заданий определяются по последней цифре номера зачетной книжки (с номера 1 по номер 8). Задания для номеров 9 -16 определяются как характеристики номеров 1-8 умноженные на 2. Далее характеристики умножаются на 3 и т.д
При выполнении задания следует учитывать, что каждый поток характеризуется только расходом. Варианты заданий приведены ниже (расходы заданы в кг-ч-1).
Порядок выполнения работы
В соответствии с индивидуальным заданием необходимо выполнить следующее.
1. Провести структурный анализ заданной ХТС.
2. Составить математическое описание элементов ХТС.
3. Составить информационную блок-схему расчета ХТС.
4. Составить алгоритм расчета ХТС методом простой итерации.
5. Выполнить расчет ХТС на ПК с использованием электронной таблицы Excel и Mathcad.
Содержание отчета
Отчет по контрольной работе должен содержать:
1. Постановку задачи.
2. Результаты структурного анализа ХТС.
3. Уравнения математического описания ХТС.
4. Информационную блок-схему расчета ХТС.
5. Алгоритм и листинги программ расчета ХТС.
6. Результаты расчета расходов для всех элементов ХТС на ПК.
7. Анализ полученных результатов.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ К КОНТРОЛЬНОЙ РАБОТЕ
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
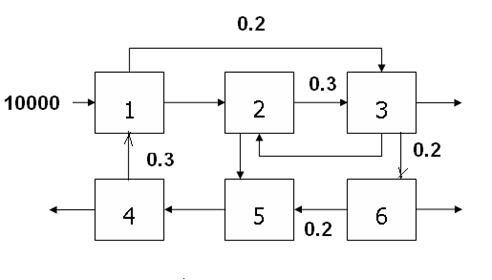
Задание 6
Задание 7
Задание 8
РАЗДЕЛ 3
Приложение
Подготовка задачи для решения в рамках EXCEL проводится в следующей последовательности:
1) выбор ячеек для поисковых переменных,
2) задание в них координат исходной точки поиска,
3) выбор ячейки для значения целевой функции,
4) запись в ней формулы для её вычисления,
5) выбор ячеек для ограничений в виде функциональных неравенств,
6) запись в ячейках формул для их вычисления,
7) выбор ячеек для ограничений в виде функциональных равенств,
8) записи в ячейках формул для их вычисления.
Далее с помощью кнопок “Сервис”, ”Поиск решения” подключается один из двух градиентных методов: метод Ньютона или метод сопряжённых градиентов. Задаются ячейки, значения которых будут варьироваться в процессе поиска, добавляются ограничения на переменные, задаются параметры поиска (число итераций, способ вычисления частных производных и т.д.). По команде “Выполнить “ осуществляется решение задачи.
Примеры решения задач оптимизации. Функция Пауэлла
Найти минимум функции 
.
На рисунке 6.1 показан предварительный этап решения задачи оптимизации.
На первом этапе выбираются произвольные ячейки (например,B1-B4) для поисковых переменных x, y, v, z. В эти ячейки вводятся координаты исходной точки поиска(5, 0.5, 0.1, 0.1).
Далее выбирается произвольная ячейка для значений целевой функции (например, С1) и в неё записывается формула для вычисления этих значений.
Далее с помощью кнопок “Сервис”, ”Поиск решения” подключается один из двух градиентных методов: метод Ньютона или метод сопряжённых градиентов (рисунок 6.2, рисунок 6.3).
После нажатия клавиши ”Добавить” задаются ограничения на переменные (рисунок 6.4).
После задания параметров поиска и нажатия клавиши ВЫПОЛНИТЬ (рисунок 6.5) происходит решение задачи с указанием состояния поиска решения на каждой итерации (рисунок 6.6). Результат решения показан на рисунке 6.7.
Рисунок 6.1 - Решение задачи оптимизации. Функция Пауэлла
Рисунок 6.2 - Подключение одного из двух градиентных методов:
метода Ньютона или метода сопряжённых градиентов
Рисунок 6.3 - Подключение одного из двух градиентных методов:
метода Ньютона или метода сопряжённых градиентов
Рисунок 6.4 - Задание ограничений на переменные
Рисунок 6.5 - Решение задачи
Рисунок 6.6 - Решение задачи с указанием решения на каждой итерации
Рисунок 6.7 - Решение задачи
