Примеры решения задач к контрольной работе № 2

 

Задача № 1

Найти интервалы монотонности и точки экстремума функции .

Решение. Точки, в которых функция определена, а ее производная либо равна нулю, либо не существует, называют критическими точками.

Данная функция определена и непрерывна при всех . Найдем ее производную:

.

Критические точки:

(в этой точке производная обращается в ноль);

(в этой точке производная терпит разрыв).

Эти точки разбивают область определения функции на интервалы (-∞;-1), (-1;0) и (0;+∞), в каждом из которых производная функции сохраняет знак. Поэтому достаточно определить знак производной в произвольной точке каждого интервала.

Для всех и выполняется неравенство . Следовательно, в интервалах и функция возрастает. Для всех выполняется неравенство . Следовательно, в интервале функция убывает.

Для наглядности поместим результаты вычислений в таблицу.

x	(-∞; -1)	-1	(-1; 0)		(0; +∞)
	+		-	Не сущ.	+
y

 

Для отыскания экстремумов функции поступают следующим образом: находят все критические точки, а затем исследуют каждую из них с целью выяснения, есть ли в этой точке минимум или максимум, или же экстремума в ней нет.

Таким образом, при переходе через точку в направлении возрастания переменной x производная меняет знак «плюс» на знак «минус». Следовательно, точка является точкой максимума и . При переходе через точку производная меняет знак «минус» на знак «плюс». Следовательно, точка является точкой минимума и .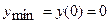

 

Задача №2

Составить уравнение касательной и уравнение нормали к данной кривой в точке с абсциссой

Решение. Уравнение касательной к кривой в точке имеет вид

,

а уравнение нормали

При получим .

Найдем заданной кривой: . Следовательно,

Уравнение касательной

или .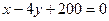

Уравнение нормали: , или .

 

Задача №3

Найти наибольшее и наименьшее значения функции на отрезке .

Решение. Если функция непрерывна на отрезке , то на этом отрезке существует точка, в которой функция принимает наибольшее значение, и точка, в которой функция принимает наименьшее значение. Причем, если функция имеет на отрезке максимумы в точках , то наибольшее значение функции на отрезке равно наибольшему из чисел

.

Аналогично, если функция имеет на отрезке минимумы в точках , то наименьшее значение функции на отрезке равно наименьшему из чисел

.

Найдем максимумы и минимумы функции на отрезке . Вычислим производную функции:

.

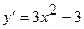Точки, подозрительные на экстремум, найдем из условия

т.е. .

Критические точки: Наличие экстремума в указанных точках определим с помощью достаточного условия экстремума. Найдем вторую производную функции:

.

Так как , а , то в точке имеется максимум, а в точке – минимум. Вычислим значения функции в точках экстремума и на концах заданного отрезка:

Таким образом, наибольшее значение рассматриваемой функции

,

а наименьшее значение функции

.

 

Задача №4

Исследовать методами дифференциального исчисления функцию

и построить ее график.

Решение. Исследование функции будем проводить, придерживаясь следующей схемы:

1) Найдем область определения функции.

Так как функция представляет собой дробь, знаменатель дроби должен быть отличен от нуля.

, .

Таким образом, .

2) Проверим, является ли функция четной, нечетной, периодической.

.

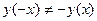Функция не является ни четной, ни нечетной. Функция не является периодической.

3) Найдем точки пересечения с осями координат.

График функции пересекает оси координат в точках и .

4) Исследуем функцию на наличие у ее графика асимптот.

I. Вертикальные асимптоты.

Поскольку функция разрывна в точке и

,

то прямая – вертикальная асимптота графика.

 

II. Наклонные асимптоты.

Наклонные асимптоты будем искать в виде прямых ,

где

.

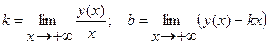
Вычислим пределы:

;

.

 

При 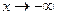значения коэффициентов k и b не изменятся. Следовательно, при график имеет наклонную асимптоту .

5) Найдем интервалы возрастания, убывания функции, точки экстремума. Вычислим первую производную функции.

 

 

.

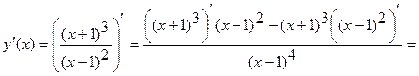
Критические точки: , , .

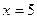Функция возрастает для тех значений переменной, при которых , убывает для тех значений переменной, при которых . Таким образом, функция возрастает на промежутках , убывает на промежутке (1;5).

Точка 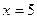является точкой минимума, .

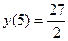6) Найдем промежутки выпуклости вверх или вниз, точки перегиба. Вычислим вторую производную функции.

.

 

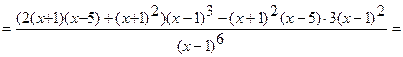
Очевидно, что при , при . Точка является точкой перегиба, .

 

7) Результаты исследования оформим в виде таблицы.

x	(-∞; -1)	-1	(-1; 1)	(1; 5)		(5; +∞)
	-		+	+		+
	+		+	-		+
	-		+	+	+	+
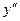
	т. п.

 

8) Строим график функции, нанося предварительно асимптоты, точки пересечения графика с осями координат, точки экстремума, точки перегиба и соединяя их плавной кривой (рис. 1).

 

 

y                   0 1 x

Рис. 1

Задача №5

Найти неопределенный интеграл.

а) Интегрирование по частям.

Для решения примеров данного пункта воспользуемся формулой интегрирования по частям:

.

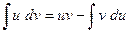Этот метод удобно применять в следующих случаях.

I. Когда подынтегральное выражение содержит в виде множителя функции , , arccos x, arctg x, arcctg x, то в качестве следует выбирать эти функции.

;

Положим , . Тогда , .

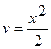Следовательно,

.

II. Подынтегральная функция имеет вид , , , где P (x) – многочлен. Если в качестве u (x) выбрать P (x), то в новом интеграле подынтегральная функция вновь будет принадлежать одному из указанных типов, но степень многочлена будет на единицу меньше.

 

.

Положим , . Тогда , а . Значит

.

К полученному интегралу снова применим формулу интегрирования по частям. Положив 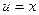, , получим , . Тогда

.

Следовательно,

 

.

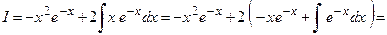
III. Подынтегральная функция имеет вид 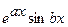, , , cos(ln x). После двукратного применения формулы интегрирования по частям, вновь получается исходный интеграл с некоторым коэффициентом. Полученное равенство является линейным алгебраическим уравнением относительно искомого интеграла.

.

Положим , . Тогда .

Имеем

.

Получили линейное относительно искомого интеграла уравнение:

,

откуда находим

.

б) Интегрирование рациональных дробей.

Напомним, что рациональной называется дробь вида , где - многочлены степеней n и m соответственно. Если 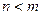, то рациональная дробь называется правильной, если - неправильной. Неправильную рациональную дробь, выделив из нее целую часть, можно представить в виде многочлена и правильной дроби.

Метод интегрирования правильной рациональной дроби состоит в разложении дроби на сумму простейших дробей и последующем интегрировании каждого слагаемого этого разложения.

.

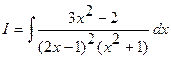Подынтегральная функция представляет собой правильную рациональную дробь. Следовательно, можно сразу производить разложение на простейшие дроби. Разложение имеет вид

,

 

где коэффициенты A, B, C, D могут быть определены методом неопределенных коэффициентов.

Приведем дроби, стоящие в правой части равенства к общему знаменателю:

и приравняем числители получившихся дробей

.

Два многочлена тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x. Приравнивая коэффициенты, получаем систему уравнений для определения A, B, C и D:

при : 2 A + 4 C = 0;

при : - A + B – 4 C + 4 D = 3;

при : 2 A + C – 4 D = 0;

при : - A + B + D = -2.

Решив эту систему, находим коэффициенты A, B, C и D:

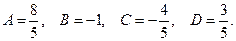
Таким образом, разложение подынтегрального выражения принимает вид:

.

Следовательно,

.

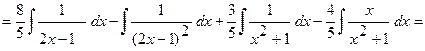
в) И нтегрирование иррациональных выражений.

С помощью подходящей подстановки подобные выражения сводят к рациональным и далее используют уже известные методы интегрирования рациональных выражений.

.

Сделаем подстановку .

Тогда .

.

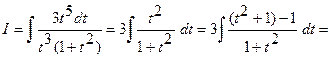
г) Интегрирование тригонометрических выражений.

При вычислении интегралов , где n, m – целые числа рекомендуется использовать следующие приемы:

I. Если оба показателя n и m - неотрицательные четные числа, то применяют формулы понижения степени:

.

 

.

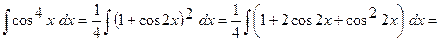
II. Если n и m - натуральные числа такие, что хотя бы одно из них нечетное, то в случае нечетного m полагают 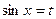, а в случае нечетного n полагают и применяют формулу

.

 

.

 

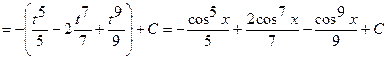Задача №6

Вычислить несобственный интеграл или показать, что он расходится.

Решение. Напомним определение несобственного интеграла. Если существует конечный предел

,

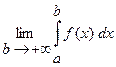то этот предел называют несобственным интегралом от функции f(x) на промежутке [a, +∞) и обозначают

.

Следовательно, по определению

.

В этом случае говорят, что несобственный интеграл сходится, в противном случае – расходится.

1)

2)

Так как полученный предел не существует, то интеграл расходится.

3)

.

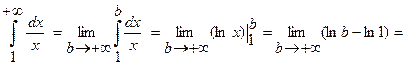
В данном случае интеграл расходится.

Задача №7

Вычислить площадь фигуры, ограниченной линиям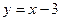и и . Сделать чертеж.

Решение. Если фигура ограничена графиками функций и 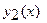и соответствующими отрезками прямых и , то ее площадь вычисляется по формуле

.

В нашем случае и , a и b – абсциссы точек пересечения указанных прямых (рис.2).

y

 

2

 

0 1 3 4

 

 

-2

 

Рис. 2

 

Найдем эти значения.

,

,

.

Найдем площадь фигуры:

.

Задача №8

Вычислить длину дуги кривой, заданной уравнениями:

а) .

б)

Решение. а) Длина дуги кривой, заданной уравнением при , вычисляется по формуле .

В рассматриваемом случае . Поэтому

.

б) Если линия задана параметрическими уравнениями

, то длина дуги этой линии вычисляется по формуле .

В рассматриваемом случае

Поэтому

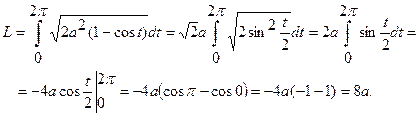
Задача №9

Вычислить объем тела, полученного при вращении вокруг оси фигуры, ограниченной линиями 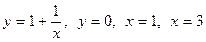. Сделать чертеж.

Решение. Объем V тела, образованного вращением вокруг оси Ox фигуры, ограниченной графиком функции , отрезками прямых и и отрезком оси , равен

.

Изобразим указанную в условии задачи фигуру (рис.3).

По формуле находим:

.

 

y

 

Рис. 3

ПРИЛОЖЕНИЕ 1

Таблица производных простейших элементарных функций.

I. (С)¢ = 0.

II. 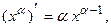в частности

III. (log _а х)¢ = log _а е, в частности (ln х)¢ = .

IV. в частности,

V. (sin х)¢ = cos х.

VI. (cos х)¢ = - sin х.

vii. ()¢ =

VIII. (ctg x)¢=

IX. (arcsin х)¢ = .

X. (arccos x)¢ = .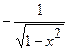

XI.(arctg x)¢ = .

XII. (arcctg x)¢ = .

XIII. (sh х)¢ = ch х.

 

XIV. (ch х)¢ = sh х.

XV. (th x) ¢ =

XVI. (cth x) ¢ =

ПРИЛОЖЕНИЕ 2

Таблица интегралов простейших элементарных функций

I.

II.

III.

IV.

V.

VI.

VII.

VIII.

IX.

X.

XI. .

XII.

XIII.

XIV.

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Пискунов Н. С. Дифференциальное и интегральное исчисления / Н.С. Пискунов.- М.: Наука, 1985. Т.1.

2. Данко П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.: Высш. шк., 1986. Ч. 1.

3. Рябушко А.П. и др. Сборник индивидуальных заданий по высшей математике / А.П. Рябушко. - Минск: Вышэйш. шк., 1990. Ч.1.

4. Каплан И.А. Практические занятия по высшей

математике / И.А. Каплан. – Харьков: ХГУ, 1973. Ч. 1, 2.

5. Кузнецов Л.А. Сборник заданий по высшей математике / Л.А. Кузнецов - М.: Высш. шк., 1994. 172 с.

 

СОДЕРЖАНИЕ

1.	Общие рекомендации студенту-заочнику к изучению курса математики................................
2.	Правила выполнения и оформления контрольных работ
3.	Программа курса “Математика” для студентов- заочников инженерно-технических специальностей....
4.	Вопросы для самопроверки к контрольной работе № 2
5.	Контрольная работа № 2.........................
6.	Примеры решения задач к контрольной работе № 2...
	Приложение 1...................................
	Приложение 2...................................
Библиографический список......................

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к контрольной работе № 2

по математике для студентов

инженерно–технических специальностей

заочной формы обучения

 

 

Составители:

Бырдин Аркадий Петрович

Иохвидов Евгений Иосифович

Сидоренко Александр Алексеевич

Томилов Марк Федорович

 

 

В авторской редакции

 

Компьютерный набор А.А. Сидоренко

Подписано в печать 18.04.2016.

Формат 60´84/16. Бумага для множительных аппаратов.

Усл. печ. л. 3,0. Уч.-изд. л. 2,8. Тираж 150 экз. “C”.

Зак. №

 

ФГБОУ ВО “Воронежский государственный технический университет”

394026 Воронеж, Московский просп., 14