Задание 5. Решить дифференциальные уравнения I порядка. А) Найти общее решение:.
Б) Найти частное решение, удовлетворяющее начальному условию: 
Задание 6. Найти общее решение дифференциального уравнения

Задание 7. Исследовать ряд на сходимость 
Задание 8. Найти область сходимости функционального ряда 
Задание 9. Вычислить приближенно определенный интеграл, используя разложение подынтегральной функции в степенной ряд и почленное интегрирование полученного ряда. Результат должен быть получен с точностью до 0,001.

Задание 10. Разложить функцию в ряд Тейлора по степеням х

Задание 1. Вычислить определенный интеграл:  .
.
Задание 2. Вычислить площадь плоской фигуры, ограниченной заданными кривыми:  .
.
Задание 3. Вычислить двойной интеграл

Задание 4. Найти объем тела, заданного ограничивающими его поверхностями 

Задание 5. Решить дифференциальные уравнения I порядка. А) Найти общее решение:  . Б) Найти частное решение, удовлетворяющее начальному условию:
. Б) Найти частное решение, удовлетворяющее начальному условию: 
Задание 6. Найти общее решение дифференциального уравнения

Задание 7. Исследовать ряд на сходимость 
Задание 8. Найти область сходимости функционального ряда 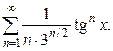
Задание 9. Вычислить приближенно определенный интеграл, используя разложение подынтегральной функции в степенной ряд и почленное интегрирование полученного ряда. Результат должен быть получен с точностью до 0,001.

Задание 10. Разложить функцию в ряд Тейлора по степеням х
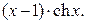
Задание 1. Вычислить определенный интеграл:  .
.
Задание 2. Вычислить площадь плоской фигуры, ограниченной заданными кривыми:  .
.
Задание 3. Вычислить двойной интеграл

Задание 4. Найти объем тела, заданного ограничивающими его поверхностями 

Задание 5. Решить дифференциальные уравнения I порядка. А) Найти общее решение:  . Б) Найти частное решение, удовлетворяющее начальному условию:
. Б) Найти частное решение, удовлетворяющее начальному условию: 
Задание 6. Найти общее решение дифференциального уравнения

Задание 7. Исследовать ряд на сходимость 
Задание 8. Найти область сходимости функционального ряда 
Задание 9. Вычислить приближенно определенный интеграл, используя разложение подынтегральной функции в степенной ряд и почленное интегрирование полученного ряда. Результат должен быть получен с точностью до 0,001.
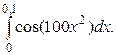
Задание 10. Разложить функцию в ряд Тейлора по степеням х.

Задание 1. Вычислить определенный интеграл:  .
.
Задание 2. Вычислить площадь плоской фигуры, ограниченной заданными кривыми:  .
.
Задание 3. Вычислить двойной интеграл

Задание 4. Найти объем тела, заданного ограничивающими его поверхностями 

Задание 5. Решить дифференциальные уравнения I порядка. А) Найти общее решение:  Б) Найти частное решение, удовлетворяющее начальному условию:
Б) Найти частное решение, удовлетворяющее начальному условию: 
Задание 6. Найти общее решение дифференциального уравнения
y ’’ – 4 y ’ + 3 y = – e 2 x sin 6 x.
Задание 7. Исследовать ряд на сходимость 
Задание 8. Найти область сходимости функционального ряда 
Задание 9. Вычислить приближенно определенный интеграл, используя разложение подынтегральной функции в степенной ряд и почленное интегрирование полученного ряда. Результат должен быть получен с точностью до 0,001.

Задание 10. Разложить функцию в ряд Тейлора по степеням х

литература
 1. Данко П.Е., Попов А.С., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. ч. I. Учеб. пособие для втузов. – М.: Высш. школа, 1996.
1. Данко П.Е., Попов А.С., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. ч. I. Учеб. пособие для втузов. – М.: Высш. школа, 1996.
2. Шипачев В.С. Задачи по высшей математике: Учеб. пособие для вузов. – М.: Высш. школа, 1996.
3. Мироненко Е.С. Высшая математика: Мет. указания и контрольные задания для студентов – заочников инженерных специальностей вузов. –М.: Высш. школа, 2000. – 110 с.
4. Пискунов Н.С. Дифференциальное и интегральное исчисление. Ч. I. – М.: Наука, 1972.
Правила оформления контрольных работ
1. Контрольная работа должна быть выполнена в отдельной ученической тетради в клетку с полями не менее 3 см для замечаний преподавателя.
2. На обложке тетради указываются фамилия, имя, отчество студента, шифр (номер студенческого билета), курс, факультет и специальность, по которой студент обучается, номер контрольной работы, год издания методических указаний, из которых взято контрольное задание.
3. Условия задачи переписываются полностью, без сокращения слов, после чего приводится подробное решение со ссылками на использованные определения, теоремы, формулы; в конце решения записывается ответ; чертежи можно выполнять аккуратно от руки.
4. В работу должны быть включены все задачи, указанные в задании, строго по варианту. Контрольные работы, содержащие не все задачи, а также задачи не своего варианта, не зачитываются.
5. Если в контрольной работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и сдать работу с исправлениями на повторную проверку.
6. Никакие исправления в тексте уже проверенной работы не допускаются, все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой относятся дополнения и исправления.
Каждую контрольную работу студент после проверки предъявляет к защите. На защите студент должен объяснить и, в случае необходимости, защитить свое решение, ответить на поставленные преподавателем вопросы по решенным в работе задачам.
Без предъявления защищенных работ студент к экзамену не допускается.






