Справочный материал.
Упорядоченная система n действительных чисел  называется n-мерным вектором. Обозначение:
называется n-мерным вектором. Обозначение:  или
или  . Числа
. Числа  называются компонентами вектора.
называются компонентами вектора.
Множество всех n -мерных векторов с действительными компонентами, рассматриваемая с определёнными в ней операциями сложения векторов и умножения вектора на число, называется n-мерным векторным пространством  .
.
Число  называется собственным значением (собственным числом) матрицы А порядка n, если существует такой ненулевой вектор
называется собственным значением (собственным числом) матрицы А порядка n, если существует такой ненулевой вектор  , что выполняется равенство
, что выполняется равенство  . При этом вектор
. При этом вектор 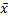 называется собственным вектором матрицы A. Данное в определении уравнение можно переписать в виде
называется собственным вектором матрицы A. Данное в определении уравнение можно переписать в виде  . Полученная однородная система всегда имеет нулевое решение. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы был равен нулю, то есть
. Полученная однородная система всегда имеет нулевое решение. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы был равен нулю, то есть  . Это уравнение называется характеристическим уравнением матрицы A.
. Это уравнение называется характеристическим уравнением матрицы A.
Пример. Найти собственные числа и собственные векторы матрицы  .
.
Решение. Найдём собственные числа матрицы. Для этого составим характеристическое уравнение:  или
или
 , корни которого
, корни которого  являются собственными чисоами матрицы.
являются собственными чисоами матрицы.
Найдём собственный вектор, соответствующий собственному числу  . Для этого значение
. Для этого значение  подставляем в уравнение
подставляем в уравнение  . Откуда получаем
. Откуда получаем  или
или  Одно из уравнений системы можно отбросить и получаем. Система имеет бесконечное множество решений. Придадим переменной
Одно из уравнений системы можно отбросить и получаем. Система имеет бесконечное множество решений. Придадим переменной 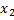 значение
значение  , тогда
, тогда  . Таким образом собственный вектор матрицы, соответствующий собственному числу
. Таким образом собственный вектор матрицы, соответствующий собственному числу  имеет вид:
имеет вид: 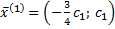 .
.
Найдём собственный вектор, соответствующий собственному числу  . Для этого значение
. Для этого значение  подставляем в уравнение
подставляем в уравнение  . Откуда получаем
. Откуда получаем  или
или  или
или  Одно из уравнений системы можно отбросить и получаем
Одно из уравнений системы можно отбросить и получаем  . Система имеет бесконечное множество решений. Придадим переменной
. Система имеет бесконечное множество решений. Придадим переменной 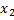 значение
значение  , тогда
, тогда  . Таким образом собственный вектор матрицы, соответствующий собственному числу
. Таким образом собственный вектор матрицы, соответствующий собственному числу  имеет вид:
имеет вид:  .
.
ЗАДАЧА 5.
Квадратичные формы
Справочный материал.
Квадратичной формой  от n переменных называется сумма, каждое слагаемое которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
от n переменных называется сумма, каждое слагаемое которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
 .
.
В матричной записи квадратичная форма имеет вид:  , где
, где  – матрица-столбец переменных, А – матрица квадратичной формы.
– матрица-столбец переменных, А – матрица квадратичной формы.
Квадратичная форма называется канонической, если все её коэффициенты 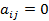 при
при  :
:  .
.
Канонический вид квадратичной формы не является однозначно определённым.
Нормальным видом квадратичной формы называют сумму квадратов нескольких неизвестных с коэффициентами +1 или –1.
Квадратичная форма L от n неизвестных с действительными коэффициентами называется положительно определённой, если она приводится к нормальному виду, состоящему из n положительных квадратов.
Квадратичная форма L от n неизвестных с действительными коэффициентами называется отрицательно определённой, если она приводится к нормальному виду, состоящему из n отрицательных квадратов.
Квадратичная форма  положительно определена тогда и только тогда, когда: все собственные значения матрицы А положительны или все главные миноры матрицы А положительны (Критерий Сильвестра).
положительно определена тогда и только тогда, когда: все собственные значения матрицы А положительны или все главные миноры матрицы А положительны (Критерий Сильвестра).
Квадратичная форма  отрицательно определена тогда и только тогда, когда: все собственные значения матрицы А отрицательны или все главные миноры матрицы А нечётного порядка отрицательны, а матрицы чётного порядка положительны (Критерий Сильвестра).
отрицательно определена тогда и только тогда, когда: все собственные значения матрицы А отрицательны или все главные миноры матрицы А нечётного порядка отрицательны, а матрицы чётного порядка положительны (Критерий Сильвестра).
Пример. Привести квадратичную форму L к каноническому виду:
 .
.
Решение.
Выполним следующие преобразования:
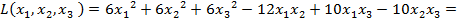


.
Выполним переобозначения:
 ,
,  ,
,  .
.
Полученное линейное преобразование  ,
,  ,
,  приводит квадратичную форму к следующему каноническому виду:
приводит квадратичную форму к следующему каноническому виду:
 .
.
Ответ:  .
.
Вопросы к экзамену (зачету)
- Комплексные числа
- Арифметические действия над комплексными числами
- Модуль и аргумент, тригонометрическая форма комплексного числа
- Возведение в степень комплексного числа и извлечение комплексного корня
- Многочлены. Разложение многочлена на множители
- Комплексные корни многочлена. Разложение многочлена на множители
- Метод Гаусса
- Решение СЛАУ
- Линейная зависимость. Ранг системы векторов
- Базис и разложение вектора по базису
- Фундаментальный набор решений однородной СЛАУ
- Скалярное произведение
- Скалярное произведение, длина вектора, угол между векторами
- Ортогональный базис
- Действия над матрицами
- Арифметические действия над матрицами, транспонирование
- Умножение матриц, возведение матрицы в степень
- Определители
- Вычисление определителя
- Ранг матрицы
- Обратная матрица
- Матричные уравнения
- Формулы Крамера
- Матрица перехода от одного базиса к другому
- Линейные операторы
- Значение линейного оператора на векторе
- Матрица линейного оператора
- Преобразование матрицы линейного оператора при переходе к другому базису
- Спектр линейного оператора
- Собственные значения и собственные векторы матрицы
- Собственные значения и собственные векторы линейного оператора
- Квадратичные формы
- Матрица квадратичной формы
- Ранг квадратичной формы
- Приведение квадратичной формы к нормальному виду
- Приведение квадратичной формы к главным осям
- Знакоопределенность квадратичной формы






