Выполнение письменной контрольной работы является обязательным условием допуска студента до устного экзамена по дисциплине «Прикладная математика».
Задания отражают краткий курс 1 модуля дисциплины и их выполнение считается обязательным при усвоении курса.
Контрольная работа выполняется в школьной тетради от руки и сдается на кафедру ФМН не позднее двух недель после изучения модуля 1. Каждое задание пишется на отдельном листе с соблюдением полей.
Рекомендуется следующий порядок выполнения контрольной работы:
1. Ознакомление с теоретическим материалом, тематику которого предстоит отразить в контрольной работе, чтобы составить представление о предмете исследования, его значении и месте в курсе математики.
2. Тщательное изучение теоретического материала, необходимого для выполнения контрольной работы.
3. Тщательное изучение практического материала, необходимого для выполнения контрольной работы, прорешивание заданий из указанной литературы на заданную тематику.
4. Непосредственное написание работы.
Номер варианта контрольной работы определяется по списку журнала посещаемости.
Работа должна быть написана грамотно и аккуратно.
Контрольная работа может быть направлена на доработку, если она не отвечает предъявленным требованиям: студент выполнил не свой вариант или неправильно решил задачи. После устранения всех соответствующих недостатков контрольная работа должна быть предоставлена на повторную проверку.
Образец ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ работы № 1
Выполнение первого задания
Разложить в ряд Фурье периодическую (с периодом Т = 2π) функцию f (х), заданную на отрезке [-π; π].
Решение.
Функция удовлетворяет условиям Дирихле, а поэтому разлагается в ряд Фурье. Найдём коэффициенты искомого ряда
.
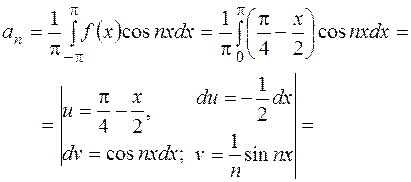
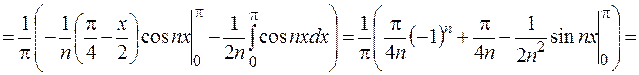
Ответ: искомое разложение функции в ряд Фурье имеет вид
.
Выполнение второго задания
Разложить в ряд Фурье периодическую (с периодом Т = 2) функцию f (х), заданную на отрезке [-1; 1].
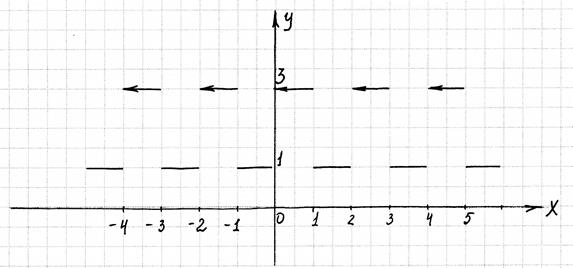
Решение.
Функция удовлетворяет условиям Дирихле, а поэтому разлагается в ряд Фурье, коэффициенты которого вычислим по известным формулам.
,
,
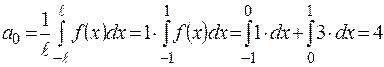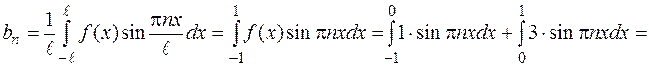
Ответ: 
.
Выполнение третьего задания
Разложить в ряд Фурье периодическую функцию f (х) =│ x │, на отрезке [-2; 2].
Решение.
f (х) =│ x │, непрерывная функция, удовлетворяющая условиям теоремы о разложимости, и, следовательно, разлагается в свой ряд Фурье. Она четная, поэтому разлагается в ряд Фурье только по косинусам, т. е. bn = 0.
Находим коэффициенты а 0 и ап искомого ряда
,
Ответ: искомый ряд Фурье данной функции
.
Выполнение четвертого задания
Разложить в ряд Фурье функцию 
, заданную на полупериоде [0; 2], продолжив (доопределив) её четным и нечетным образом. Построить графики функций.
Решение.
1. Доопределим функцию f (x) на отрезке [-2; 0] четным образом
Для четной функции коэффициенты bn = 0, а коэффициенты an вычисляются по формулам
.
,
Тогда
.
2. Доопределим функцию f (x) на отрезке [-2; 0] нечетным образом
Для нечетной функции коэффициенты a 0 = an = 0, находим коэффициенты bn.
.
Тогда
.
Ответ: 1. .
2. .
Выполнение пятого задания
Разложить в ряд Фурье функцию f (x), с периодом 4; график функции в интервале (-2; 2) изображён на чертеже
Решение.
Заданная функция нечетная с периодом 
, поэтому a0 = an = 0.
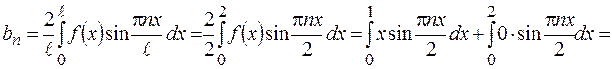
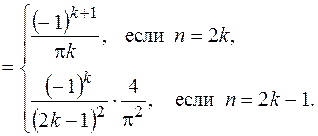
Ответ: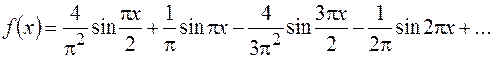 
.
