Однократные измерения физической величины и оценка погрешностей результата однократного измерения

Министерство образования и науки Российской

Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Таганрогский государственный радиотехнический

университет

 

 

 

СБОРНИК РУКОВОДСТВ

 

к лабораторным работам

по курсу

 

МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ

И СЕРТИФИКАЦИЯ

 

Для студентов, обучающихся по направлениям

 

Информатика и вычислительная техника,

Проектирование и технология электронных средств,

Автоматизация и управление, Приборостроение

 

 

 

ТАГАНРОГ 2005

 

УДК 389.1(076.5)+389.6(076.5)+658.562(076.5)

 

Составители: В.Г. Косторниченко, В.Б.Лапшин

 

Сборник руководств к лабораторным работам по курсу «Метрология, стандартизация и сертификация». – Таганрог: Изд-во ТРТУ, 2005. – 52 с.

 

Данный сборник содержит основные термины, понятия и определения метрологии и руководства к выполнению четырех лабораторных работ. Руководства включают основные теоретические сведения, методики выполнения, требования к отчету и контрольные вопросы.

 

 

Рецензент С.В.Кавчук, доцент кафедры АСНИ и Э ТРТУ.

 

 

Основные понятия и определения

 

1.1. Физической величиной называется одно из свойств физического объекта (физической системы, явления, процесса), общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них.

Количественное содержание этого свойства в объекте является размером физической величины, а числовую оценку ее размера называют значением физической величины.

1.2. Физическую величину характеризует ее истинное значение, которое идеальным образом отражает в количественном и качественном отношениях соответствующее свойство объекта. Действительным называют значение физической величины, найденное экспериментально и настолько приближающееся к истинному значению, что для данной измерительной задачи оно может быть использовано вместо него.

1.3. Значение величины, полученное путем ее измерения, называют результатом измерения.

Согласно РМГ 29–99 «Рекомендации по межгосударственной стандартизации», измерение – совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающего нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.

1.4. По способу получения числового значения измеряемой величины (информации) все измерения делят на прямые, косвенные, совокупные и совместные.

Прямым называют измерение, при котором искомое значение величины находят непосредственно из опытных данных. Примерами прямых измерений являются измерения вольтметром напряжения источника, длины тела линейкой и т. д. Таким образом, при прямых измерениях экспериментальным операциям подвергают измеряемую величину, которую сравнивают с мерой непосредственно или с помощью измерительных приборов, градуированных в требуемых единицах с помощью меры.

Косвенным измерением называют измерение, результат которого определяют на основании прямых измерений величин, связанных с измеряемой величиной известной зависимостью.

Уравнение косвенного измерения имеет вид

, (1.1)

где Y – искомая величина, являющаяся функцией аргументов 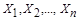, измеряемых прямым методом.

Совокупными называют измерения, при которых проводятся одновременно измерения нескольких одноименных величин с определением искомой величины путем решения системы уравнений. Число уравнений системы не должно быть меньше числа искомых величин.

Совместными называютизмерения, при которых одновременно проводятся измерения не одноименныхфизических величин с целью нахождения зависимости между ними.

1.5. Техническое средство, предназначенное для измерений, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени, имеющее в этих целях нормированные метрологические характеристики, называется средством измерений. При этом под метрологической характеристикой средства измерений понимается характеристика одного из свойств средства измерений, влияющая на результат измерения и на его погрешность.

Метрологические характеристики, устанавливаемые нормативными документами, называют нормируемыми метрологическими характеристиками, а определяемые экспериментально – действительными метрологическими характеристиками.

Средства измерений, предназначенные для получения значений измеряемой физической величины в установленном диапазоне, называются измерительными приборами. Измерительный прибор, показания которого являются непрерывной функцией изменений измеряемой величины, называется аналоговым измерительным прибором. Например, электроизмерительный прибор с отсчётным устройством в виде стрелки и шкалы. Измерительный прибор, автоматически вырабатывающий дискретный (кодированный) сигнал измерительной информации и дающий показания в цифровой форме, называют цифровым измерительным прибором. Измерительные приборы, реализующие метод непосредственной оценки, называют приборами прямого действия (амперметры, вольтметры и др.). Приборы, реализующие метод сравнения с мерой, называют приборами сравнения (мосты, компенсаторы и др.).

1.6. Результат измерения практически всегда отличается от истинного значения физической величины. Это отличие объясняется несовершенством средств измерений, несовершенством способов их использования, влиянием внешних условий, участием человека с ограниченными возможностями и т.д.

Отклонение результата измерения от истинного (действительного) значения измеряемой величины называется погрешностью измерения:

, (1.2)

где X – измеренное значение, – истинное значение, – действительное значение.

1.7. По причинам возникновения погрешности подразделяются на систематические и случайные.

Систематическими () называются погрешности, которые при повторных измерениях одной и той же физической величины остаются постоянными или изменяются закономерно, обычно прогрессируя. Одной из распространенных систематических погрешностей является погрешность градуировки (погрешность нанесения делений на шкалу измерительного прибора), которая легко выявляется и для её устранения составляется таблица поправок. По определению, поправкой называется величина, которую нужно прибавить к показаниям прибора, чтобы получить действительное значение измеряемой величины, т.е. . Очевидно, что . Систематическими погрешностями также являются методические погрешности. Систематические погрешности могут быть в значительной степени исключены или уменьшены устранением источников погрешностей или введением поправок. Следует иметь в виду, что полностью исключить систематические погрешности невозможно, поэтому всегда остаётся неисключенный остаток систематической погрешности (НСП).

Случайными () составляющими погрешности результата измерения называются погрешности, изменяющиеся случайным образом (по значению и знаку) при повторных измерениях, проведенных с одинаковой тщательностью одной и той же физической величины. В процессе любого измерения присутствуют многочисленные влияющие факторы (температура, давление, влажность, наводки от внешних электрических полей), учесть совместное воздействие (случайную комбинацию воздействий) которых невозможно, а результат их влияния на получающуюся погрешность измерения может оказаться значительным. В связи с этим до проведения измерения предсказать значение получающейся случайной погрешности невозможно.

1.8. Погрешности измерений определяются, главным образом, погрешностями средств измерений, но они не тождественны им. По происхождению различают инструментальные и методические погрешности. Инструментальные погрешности возникают вследствие недостаточно высокого качества элементов средств измерений. Следует отметить, что инструментальная погрешность индивидуальна для каждого средства измерений. Причиной возникновения методических погрешностей служит несовершенство избранного метода измерений.

Каждое средство измерений работает в сложных, изменяющихся во времени условиях. Наряду с чувствительностью к измеряемой величине, средство измерений имеет некоторую чувствительность и к не измеряемым, но влияющим на показания величинам, например к температуре, атмосферному давлению, ударам, тряске, электрическим и магнитным полям и т.д. При выполнении измерений в лабораторных условиях, при производстве градуировки или аттестации большинство влияющих величин может поддерживаться в узких пределах их изменения. Условия измерения, характеризуемые совокупностью значений или областей значений влияющих величин, при которых изменением результата измерения пренебрегают вследствие малости, называются нормальными, а суммарная результирующая погрешность, возникающая в этих условиях, – основной погрешностью (D_о). Нормальные условия измерений устанавливаются в нормативных документах на средства измерений конкретного типа.

1.9. При эксплуатации средств измерений на производстве возникают значительные отклонения от нормальных условий, вызывающие дополнительные погрешности (D_доп).

Дополнительные погрешности нормируются указанием коэффициентов влияния изменений отдельных влияющих величин на изменение показаний в виде h _q(%/10⁰C), h_U (%/10% ) и т.д. Часто в выражении для коэффициента влияния изменения показаний указываются в долях основной погрешности, например, h _q = 0,5D₀/10⁰ C, h_U =0,3D₀/10%D U / U и т.д. Хотя фактически эти функции влияния, как правило, нелинейны (на что указывает ГОСТ 8.009–84, который рекомендует указывать функцию влияния влияющих величин на дополнительную погрешность), для простоты вычислений на практике до настоящего времени их приближенно считают линейными, и возникающие дополнительные погрешности определяют как D_доп = h Dq, где h – коэффициент влияния, а Dq – отклонение влияющих факторов от значений, указанных в нормальных условиях. Таким образом определяют дополнительные погрешности для всех влияющих величин.

При технических однократных измерениях параметров производственных процессов дополнительные погрешности могут задаваться своими границами с учетом возможных влияющих величин.

Погрешность прибора в реальных условиях его эксплуатации называется эксплуатационной и складывается из его основной погрешности и всех дополнительных

D _{i доп. (1.3)}

1.10. Абсолютная погрешность прибора D – это разность между показанием прибора и истинным (действительным) значением измеряемой величины, выраженная в ее единицах

, (1.4)

где X _п – показание прибора, X_д – действительное значение измеряемой величины.

1.11. Относительная погрешность измерительного прибора d – это отношение абсолютной погрешности к истинному (действительному) значению измеряемой величины

, (1.5)

так как действительное значение измеряемой величины и показания прибора близки по величине.

1.12. Приведённая погрешность измерительного прибора g – это отношение абсолютной погрешности измерительного прибора к нормирующему значению

. (1.6)

1.13. Нормирующее значение – это условно принятое значение, постоянное во всем диапазоне измерения или в части диапазона, равное или верхнему пределу измерения или длине шкалы и т.д. Правила выбора нормирующего значения приводятся в ГОСТ 8.009-84.

1.14. Для того чтобы ориентироваться в метрологических свойствах конкретного средства измерения, чтобы заранее оценить погрешность, которую внесёт данное средство в результат измерения, пользуются нормируемыми метрологическими характеристиками, под которыми понимается совокупность метрологических характеристик данного типа средств измерений, устанавливаемая нормативными документами на средства измерений, и точностными характеристиками, представляющими совокупность метрологических характеристик средств измерений, влияющих на точность измерения. Номенклатура метрологических характеристик, правила их выбора и отражения для конкретных типов средств измерений в нормативной документации (НД) устанавливает ГОСТ 8.009 – 84 «ГСИ. Нормируемые метрологические характеристики средств измерений».

Основная метрологическая характеристика средства измерения – это класс точности, который является обобщенной характеристикой данного типа средств измерений, как правило, отражающей уровень их точности. Класс точности выражается пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.

Способы установления пределов допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ.8.401-80 “ГСИ. Классы точности средств измерений”. Основная погрешность нормируется четырьмя различными способами, что обусловлено разным соотношением аддитивной и мультипликативной составляющих общей погрешности средств измерений.

1. При чисто мультипликативной полосе погрешностей абсолютная погрешность D_м возрастает прямо пропорционально текущему значению измеряемой величины Х. Поэтому относительная мультипликативная погрешность или погрешность чувствительности такого средства измерений

(1.7)

оказывается величиной постоянной при любом значении Х и используется для нормирования погрешностей и указания класса точности. Класс точности при этом указывается в виде значения _, выраженного в процентах. Абсолютная погрешность определяется по формуле

. (1.8)

Для этого случая, кроме значения , указываются границы рабочего диапазона измеряемой величины, в пределах которых такая оценка оказывается справедливой.

2. При чисто аддитивной полосе погрешностей остаётся неизменной при любых значениях Х граница абсолютной погрешности нуля D_о. Так как нормировать абсолютные значения погрешности неудобно, то нормируют приведённое значение этой погрешности

, (1.9)

где C_N – нормирующее значение. Значение приведённой погрешности , выраженное в процентах, используется для обозначения класса точности таких средств измерений. Текущее значение относительной погрешности

(1.10)

растёт обратно пропорционально Х (рис.1.1) и при Х = D₀ d = 100%.

3. При одновременном присутствии аддитивной и мультипликативной составляющих текущее значение абсолютной погрешности определяется двучленной формулой

, (1.11)

где D₀ – аддитивная, а C – мультипликативная составляющие абсолютной погрешности ( в этом случае указывается в относительных единицах).

 

Рис.1.1

Разделив все члены этого уравнения на верхний предел диапазона измерения , получим приведённую погрешность для этого случая:

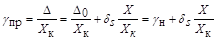, (1.12)

где

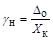(1.13)

называется приведённой аддитивной погрешностью в начале диапазона. Относительное значение погрешности при этом будет равно

. (1.14)

Отсюда следует, что при эта погрешность будет равна

. (1.15)

Класс точности таких приборов обозначается двумя числами, записываемыми через косую черту 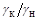, где – приведённая погрешность в конце диапазона, а 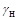– приведённая погрешность в начале диапазона. Обе погрешности выражаются в процентах.

4. ГОСТ 8.401-80 разрешает использовать специальные формулы нормирования погрешностей. Например, в измерительных приборах с очень широким диапазоном измерения полоса погрешностей определяется трехчленной формулой

, (1.16)

где – постоянное значение, присущее данному измерительному прибору, при котором погрешность достигает 100% из-за потери чувствительности к изменению больших значений измеряемой величины.

Предельное значение относительной погрешности будет равно

. (1.17)

Согласно ГОСТ 8.401–80 для указания нормированных значений погрешностей , , 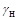не могут использоваться произвольные цифры. Выраженные в процентах они могут выбираться из ряда чисел , где А = 1; 1,5; 2; 2,5; 4; 5 и 6; n = 1; 0; -1; - 2; ….

Если же для указания погрешности используются специальные формулы, то могут использоваться и другие числа.

1.15. Значение класса точности прибора маркируется на его шкале. При этом используются следующие условные обозначения.

1.15.1. Если класс точности прибора установлен по значению погрешности чувствительности d _s (погрешность чисто мультипликативная), то обозначаемое на шкале значение класса точности обводится кружком. Например, обозначает, что d_s = ± 1,5%.

1.15.2. Если полоса погрешностей принята аддитивной и прибор нормируется по приведённой аддитивной погрешности g₀ (таких приборов большинство), то класс точности указывается без каких-либо подчеркиваний. Например, число 1,5 обозначает, что g₀ = ± 1,5%.

1.15.3. При нормировании погрешностей сложных средств измерений двухчленной формулой ГОСТ 8.401-80 предусматривает несколько иное её написание через значения g_н и g_к. Так как = g_к – g_н, то

. (1.18)

В технической литературе часто g_к обозначают через с, а g_н – через d. Тогда эта формула приобретает вид

; (1.19)

например, 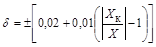означает, что класс точности этого средства измерений 0,02/0,01.

Обозначение класса точности в виде дроби 0,02/0,01 указывает, что погрешность прибора нормирована по двухчленной формуле с g_н = ± 0,01% и g_к = ± 0,02%.

1.15.4. Для трехчленной формулы погрешности в паспорте этого прибора указывают нормированные значения D₀, d _s и C _¥.

Таким образом, обозначение класса точности прибора даёт достаточно полную информацию для вычисления предельной оценки погрешности результатов измерения.

1.16. Результат измерения имеет ценность лишь тогда, когда можно оценить его интервал неопределённости, т.е. степень достоверности. Степень достоверности результата измерения оценивается доверительной вероятностью – вероятностью, с которой истинное значение измеряемой величины находится внутри доверительного интервала.В свою очередь, доверительный интервал – это интервал, который содержит истинное значение измеряемой величины с определенной доверительной вероятностью.

Поэтому согласно МИ 1317 – 86 «ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров» сообщение о любом результате измерений должно сопровождаться указанием его погрешности и доверительной вероятности. Вычисляться должна как абсолютная, так и относительная погрешности результата измерения, так как первая из них нужна для округления результата и его правильной записи, а вторая – для однозначной сравнительной характеристики его точности.

Рассчитывая значения погрешности, особенно при использовании электронного калькулятора, значения погрешностей получают с большим числом знаков. Однако исходными данными для расчета являются нормированные значения погрешности средств измерений, которые указываются с одной или двумя значащими цифрами.

Вследствие этого в окончательном значении рассчитанной погрешности должны быть оставлены только первые одна - две цифры.

Существует три правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения.

Погрешность результата измерения указывается двумя значащими цифрами, если первая из них 1 или 2, и одной, если первая есть 3 и более.

Результат измерения округляют до того же десятичного разряда, которым оканчивается округлённое значение абсолютной погрешности.

Округление производится лишь в окончательном ответе, а все предварительные вычисления производятся с одним-двумя лишними знаками.

 

Лабораторная работа № 1.

Однократные измерения физической величины и оценка погрешностей результата однократного измерения

 

Цель работы. Ознакомление со способами оценки основных и дополнительных погрешностей результата однократного измерения.

 

Методические указания.

 

2.1.1. Однократное измерение – это измерение, выполненное один раз. Во многих случаях на практике выполняются именно однократные измерения. Например, измерение конкретного момента времени по часам обычно производится один раз. При этом велика возможность грубой ошибки (промаха).

Однократные измерения характерны для производственных процессов. Поскольку измерения выполняются без повторных наблюдений, то нельзя отделить случайную погрешность от систематической составляющей (см. п. 1.7). Поэтому для оценки погрешности дают лишь ее границы с учетом возможных влияющих величин. Последние оценивают своими границами, но не измеряют. На практике дополнительные погрешности (см. п. 1.9), как правило, не учитываются, так как измерения осуществляются в основном в нормальных условиях, а субъективные погрешности также весьма малы.

2.1.2. Согласно МИ 1552 – 86 «ГСИ. Измерения прямые однократные. Оценивание погрешностей результатов измерений» однократные измерения достаточны, если неисключенная систематическая погрешность (например, класс точности СИ) заведомо больше случайной. Практически это достигается при . Тогда результат измерения записывается в виде

при вероятности , (2.1)

где – результат, зафиксированный СИ; – суммарная неисключенная систематическая погрешность измерения, определяемая классом точности СИ , методической и дополнительными погрешностями.

2.1.3. Оценка погрешности результата однократного измерения зависит от того, каким образом нормированы предельные погрешности средства измерения, т.е. от его класса точности.

Правила вычисления пределов основной погрешности средств измерений и примеры обозначения для них классов точности приведены в табл. 2.1.

 

Таблица 2.1

Обозначения классов точности средств измерений

 

Формула для вычисления пределов основной погрешности	Пределы допускаемой основной относительной погрешности, %	Примеры обозначения класса точности
Общий вид	Пример
			2,5

 

Для разных способов нормирования погрешностей средства измерений эти вычисления производятся по–разному, поэтому рассмотрим три характерных случая.

1. Класс точности указан в виде числа , заключённого в кружок. Тогда относительная погрешность результата в процентах , а абсолютная погрешность

. (2.2)

2. Класс точности указан одним числом (без кружка). Тогда абсолютная погрешность результата измерения

, (2.3)

где – нормирующее значение, а относительная погрешность определяется как

. (2.4)

В этом случае необходимо зафиксировать значение , иначе впоследствии нельзя будет вычислять погрешность результата.

3. Класс точности прибора указан двумя числами в виде дроби (). В этом случае удобно сначала вычислять относительную погрешность d, а затем найти абсолютную

. (2.5)

2.1.4. Рассмотрим несколько примеров.

Пример 1. Для измерения падения напряжения постоянного тока использовался вольтметр класса точности 0,5 с верхним пределом диапазона измерения = 1,5 В и имеющий сопротивление Ом. Известно, что дополнительные погрешности показаний СИ из-за влияния магнитного поля и температуры не превышают соответственно и .

Показание вольтметра = 0,9 В на сопротивлении R = 4 Ом.

Оценим погрешность результата измерения:

а) класс точности вольтметра указан одним числом 0,5 без кружка. Поэтому предел допускаемой относительной погрешности вольтметра, в соответствии с (2.4), на отметке 0,9 В составляет

;

б) при подсоединении вольтметра изменился ток , протекающий через сопротивление , так как часть тока стала протекать через сопротивление вольтметра . Изменилось и измеряемое падение напряжения на сопротивлении (рис. 2.1), поэтому показание вольтметра составляет

.

Тогда методическая погрешность, обусловленная конечным значением , в относительной форме будет равна

;

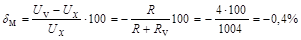в) данная методическая погрешность является систематической составляющей погрешностью измерения и должна быть внесена в результат в виде поправки, равной абсолютной методической погрешности с обратным знаком . На отметке 0,9 В поправка составит

В.

Тогда результат измерения с учетом поправки будет равен

В;

г) поскольку основная и дополнительная погрешности заданы своими граничными значениями, то они могут рассматриваться как неисключенные систематические. Для доверительной вероятности доверительная граница неисключенной систематической составляющей будет

,

а в абсолютной форме

В;

Рис. 2.1

 

д) оставим в результате измерения три цифры после запятой, в соответствии с правилами, и запишем окончательный итог измерения в виде

В; В; .

Пример 2. Для измерения напряжения постоянного тока использовался цифровой универсальный вольтметр В7 – 16А. Его класс точности , входное сопротивление 10 МОм, нормальные температурные условия эксплуатации 20±5 °С.

Показания вольтметра на пределе измерения 10 В и на измеряемом сопротивлении R = 1000 Ом В. Рабочая температура окружающего воздуха .

Оценим погрешности измерения напряжения и запишем итог измерения.

а) класс точности вольтметра указан двумя числами. Поэтому предел допускаемой относительной погрешности вольтметра в точке 8,223 В составляет

;

б) при подсоединении вольтметра измеряемое напряжение (рис. 2.1) изменилось из-за наличия , а показания вольтметра составляют (см. п. 2.1.4 б)

.

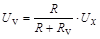Тогда методическая погрешность, обусловленная конечным значением , в относительной форме составит

.

Данная методическая погрешность на порядок меньше основной погрешности, поэтому ею можно пренебречь;

в) дополнительная температурная погрешность отсутствует, так как измерение выполнялось в нормальных температурных условиях эксплуатации 20±5 °С;

г) вычисляем абсолютную основную погрешность измерения

В;

д) округлим значение погрешности до одного значащего разряда, оставим в результате измерения три цифры после запятой в соответствии с правилами и запишем окончательный итог измерения в виде

В; В; .

 

2.2. Порядок выполнения лабораторной работы

 

2.2.1. Соберите схему, показанную на рис. 2.2. На данной схеме источник питания постоянного тока (ИП) типа Б5 – 47 используется в качестве источника тока. Для этого переключатель «V» необходимо установить в положение 25,0 В. Положение переключателя «А» указывается в соответствующем пункте методики.

Генерируемый источником ток протекает через сопротивление R, создавая на нем падение напряжения . Значение сопротивления R задается магазином сопротивлений (МС).

Падение напряжения измеряется вольтметром эталонным (ВЭ) типа РВ7 – 22А. Класс точности вольтметра 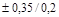. Входное сопротивление на пределе 20 В равно 10 МОм. Нормальные температурные условия эксплуатации 20 °С. Дополнительная температурная погрешность 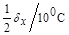, где – предел допускаемой основной относительной погрешности , %.

Для измерения падения напряжения при соответствующем подключении могут использоваться вольтметры рабочие (ВР1) типа Э59 и (ВР2) типа М367. Метрологические характеристики этих вольтметров указаны на циферблатах.

 

Рис.2.2

 

2.2.2. Выполните измерения падения напряжения на сопротивлении R с помощью ВЭ. Для этого проделайте следующее:

а) установите на выходе ИП с помощью переключателя «А» допустимый ток 0,02 А;

б) включите ИП;

в) установите значение № 1 сопротивления R из табл. 2.2;

г) зафиксируйте показание 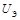ВЭ и занесите его в табл. 2.2;

Таблица 2.2

Измерения с помощью ВЭ (РВ7 – 22А)

 

№	R, Ом	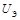, В	Относит. систем. погрешность	Метод. погрешность	Суммарная погрешность ВЭ, В	Результат измерения, В

 

д) повторите пп. 2.2.2, в, г для последующих значений сопротивлений из таблицы 2.2;

е) выключите ИП;

ж) для каждого измеренного значения падения напряжения 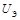вычислите предел допускаемой основной относительной погрешности , дополнительную погрешность, методическую и суммарную погрешности;

з) оформите результаты измерений для каждого значения сопротивления R.

Примечание: пункты 2.2.2, ж, з могут выполняться при домашнем оформлении отчета по лабораторной работе.

2.2.3. Выполните измерения падения напряжения на сопротивлении R с помощью ВЭ и ВР1. Для этого установите с помощью переключателя «А» ток ИП 0,20 А и проделайте следующее:

а) включите ИП;

б) установите значение № 1 сопротивления R из табл. 2.3;

в) зафиксируйте показание 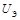ВЭ и занесите его в табл. 2.3;

Таблица 2.3

Измерения с помощью ВР1 (Э59)

 

№	R, Ом	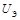, В	, В	, В	Метод. погрешность , В	Суммарная погрешность ВР1, В	Результат измерения, В

 

г) подключите параллельно ВЭ вольтметр рабочий ВР 1 (Э59);

д) зафиксируйте измененное показание ВЭ и показание ВР1 и занесите их в табл. 2.3;

е) отсоедините ВР1;

ж) выполните пункты 2.2.3, б, в, г, д, е для всех последующих значений сопротивления R из табл. 2.3;

з) выключите ИП;

и) для каждого измеренного значения вычислите предел допускаемой основной относительной погрешности , методическую абсолютную погрешность в виде разности и суммарную погрешность вольтметра ВР1;

к) оформите результаты измерений для каждого значения сопротивления R.;

л) постройте график зависимости методической погрешности вольтметра ВР1 от значения сопротивления R.

Примечание: пункты 2.2.3, е, ж, з могут выполняться при домашнем оформлении отчета по лабораторной работе.

2.2.4. Выполните измерения падения напряжения на сопротивлении R с помощью ВЭ и ВР2. Для этого установите с помощью переключателя «А» ток на выходе ИП 0,02 А и выполните пункт 2.2.3, заменяя вольтметр ВР1 на ВР2, табл. 2.3. на табл. 2.4, на , на .

Таблица 2.4

Измерения с помощью ВР2 (М367)

 

№	R, Ом	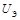, В	, В	, В	Метод. погрешность , В	Суммарная погрешность ВР2, В	Результат измерения, В

 

 

2.3. Требования к отчету

 

Отчет должен содержать:

· сведения о цели и порядке выполнения работы;

· сведения об использованных методах измерений;

· сведения о характеристиках использованных средств измерений;

· схемы включения приборов при выполнении измерений;

· экспериментальные данные;

· полностью заполненные таблицы по рекомендованной форме, а также примеры расчетов, выполнявшихся при заполнении таблиц;

· графики требуемых зависимостей;

· анализ полученных данных и вывод об особенностях и качестве проведенных измерений и результатах проделанной работы.

 

Контрольные вопросы

 

1. Дайте определение следующим понятиям: измерение, результат измерения, абсолютная погрешность измерения, относительная погрешность измерения, приведенная погрешность измерения (см. пп. 1.3, 1.6, 1.10, 1.11 и 1.12).

2. В каких случаях проводят однократные измерения? (См. п. 2.1.1).

3. Что такое средство измерений? (См. п. 1.5).

4. Что такое инструментальные погрешности? методические погрешности? основные и дополнительные погрешности? (См. пп. 1.8 и 1.9).

5. Что такое метрологические характеристики средств измерений? Какие метрологические характеристики средств измерений вы знаете? Как связаны метрологические характеристики средств измерений с их классом точности? (См. п.1.14).

 

 

Лабораторная работа № 2.