Maximum error is 4.4764192e-13

ЗАДАНИЯ ПО ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКЕ

для заочников

Задания оформляются в отдельной тетради, на обложке которой кроме фамилии и номера группы должны быть указаны следующие данные:

a =, b =, g =, q =, m =, n =.

Здесь a - номер института, b– год поступления, g и q– две последние цифры номера группы, m и n– две цифры номера студента по списку.

Так, у пятого студента группы 725311 a = 7, b = 5, g = 1, q = 1, m = 0, n = 5 .

В тетради должно быть записано условие задания и его подробное решение. Если в задании предполагается использовать интегрированные среды (Eureka, Scilab), то в тетради необходимо записать содержимое окон соответствующей среды (Edit, Solution – для Eureka и Editor, Scilab Command Window – для Scilab). Тексты программ на алгоритмическом языке (Pascal, Scilab) вместе с результатом решения задач в интегрированной среде (Turbo Pascal, Scilab) также следует записать в тетрадь.

ЗАДАНИЕ 1

Методом деления отрезка пополам и методом касательных (Ньютона) уточнить корень уравнения с погрешностью e = 0.1

a) 0.25(a+ b+ g+ q) x ³ –2 x ² + 2.3 x –N_ст = 0

Это же уравнение решить с помощью интегрированных сред Eureka и Scilab.

Пример выполнения задания 1: (вариант а, номер студента N_ст= 55),

уравнение, которое нужно решить: 65 – ln x – x = 0

Решение уравнения приближенными методами состоит из двух этапов. Первый этап – отделение корня. Отделить корень уравнения f (x) = 0 – значит найти такой отрезок [ a, b ], на котором содержится только один корень уравнения. Отделить корень можно графически и аналитически. Чтобы отделить корень аналитически, достаточно найти такой отрезок [ a, b ], на котором выполняются три условия:

1) f (a)ž f (b) < 0,

2) f (x) – непрерывная на отрезке [ a, b ] функция,

3) f (x) – монотонная на отрезке [ a, b ] функция.

Эти условия – достаточные для того, чтобы на отрезке [ a, b ] был отделен корень уравнения f (x) = 0.

Чтобы найти отрезок [ a, b ], на котором выполняется первое из условий, можно протабулировать функцию f (x) = 65 – ln x – x c некоторым шагом h до тех пор, пока функция не сменит знак. Это можно сделать с помощью ИС Eureka (Scilab).

Чтобы протабулировать функцию с помощью ИС Eureka, надо подать команду Graph 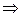Function, ввести с клавиатуры функцию f (x) = 65 – ln(x)– x, подать команду List, указать первое значение аргумента (First point), например, 40, шаг (приращение аргумента) (Increment), например, 1 и количество значений аргумента (Number of value), например, 30. В результате откроется окно с таблицей значений функции в указанном интервале. Это окно можно «распахнуть» на весь экран клавишей F5. Из приведенного листинга функции видно, что смена знака происходит на отрезке [60, 61]:

f( 60) = 65 – ln 60 – 60 » 0.906, f (61) = 65 – ln 61 – 61 » – 0.111.

f (x) = 65 – ln x – x – непрерывная функция для любых x > 0, в том числе она непрерывна и на отрезке [60, 61].

Чтобы проверить монотонность функции f (x) = 65 – ln x – x на этом отрезке, найдем ее производную f ¢(x) = – 1 /x –1. Очевидно, что для любого x > 0 y¢ < 0, следовательно, функция f (x) = 65 – ln x – x монотонно убывает на отрезке [60, 61]. Вывод: поскольку на отрезке [60, 61] выполняются условия 1 – 3, корень на нем отделен.

Второй этап решения – это уточнения корня уравнения заданным методом(в нашем случае – методом деления отрезка пополам и методом касательных) с заданной погрешностью (в нашем случае e = 0.1). Рассмотрим сначала метод деления отрезка пополам.

Согласно этому методу отрезок, на котором отделен корень уравнения, делят пополам и выбирают для дальнейших вычислений ту половину, на концах которой функция принимает значения разных знаков.

Составим следующую таблицу:

№ итерации a 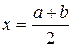b f (a) f (x) f (b)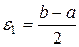

60.5 0.91 0.40 –0.11 0.5

60.5 60.75 0.40 0.14 –0.11 0.25

60.75 60.88 0.14 0.01 –0.11 0.13

60.88 60.94 0.06

Все расчеты в таблице приведены с двумя знаками после запятой.

Пояснения к таблице.

В первой строке таблицы a = 60, b = 61 – исходный (начальный) отрезок, 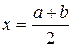–его середина, f (a), f (b), f (x) – значения нашей функции f (x) = 65 – ln x -- x в указанных точках. Если в качестве корня взять значение x = 60.5, то погрешность, с которой мы его уточнили, равна e ₁= 0.5, то есть корень уравнения x = 60.5±0.5. Поскольку e ₁ >e = 0.1, делаем вторую итерацию. Следующий отрезок, который мы будем делить пополам, – это либо [ a, x ], либо [ x, b ]. В нашем случае это отрезок [ x, b ], так как f (x)ž f (b) < 0, тогда как f (a)ž f (x) > 0. И т.д.

После четвертой итерации погрешность e ₁ = 0.06 < e, поэтому можно сделать вывод о том, что корень уравнения 65 – ln x – x = 0 равен x = 60.94±0.06.

Ответ: x = 60.94 ± 0.06

Рассмотрим теперь метод касательных. При его использовании для уточнения корня уравнения приближенное значение корня на каждой итерации вычисляют по формуле Ньютона

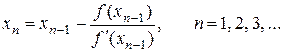
В качестве начального приближения 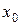выбирают тот конец отрезка [ a, b ], в котором выполняется условие

.

В нашем случае 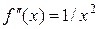, и, следовательно, 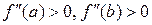, но (см. выше) f (a)>0, f (b)<0, следовательно, 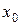= a. Тогда, полагая в формуле Ньютона n =1, получим

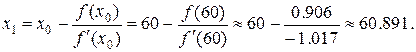
Для оценки погрешности полученного значения корня 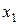можно воспользоваться формулой

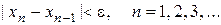
Получим 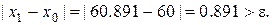Продолжая вычисления по формуле Ньютона при n =2, на второй итерации будем иметь

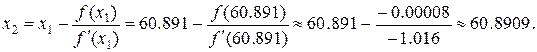
Так как 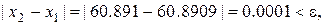то вычисления прекращаем. Задание выполнено.

Ответ: x = 60.8909 ± 0.0001

Чтобы решить уравнение 65 – ln x – x = 0на отрезке [60, 61] в ИС Eureka, достаточно в окне Edit набрать следующие строки:

65 –ln(x)– x = 0

60<= x <=61

после чего с помощью клавиши Esc войти в основное меню и выполнить команду Solve. В окне Solution появится ответ:

x = 60.890916

Maximum error is 4.4764192e-13

Последняя строка означает, что если подставить полученное значение x в уравнение, то получится число, отличающееся от нуля по модулю на 4.4764192ž10^-13.

Ответ: x = 60.890916

Напоминаем, что содержимое окон Edit и Solution во всех заданиях нужно переписывать в тетрадь.

Покажем, как выполнить задание 1 с помощью интегрированной среды Scilab (основные принципы работы с Scilab изложены на с.23 – 38; на с.39 приведен краткий перечень некоторых математических функций Scilab, используемых при выполнении заданий).

Для решения уравнений, в том числе трансцендентных, в Scilab применяют функцию fsolve(x0,f), где x0 - начальное приближение, f - функция, описывающая левую часть уравнения f(x)=0.

Для нахождения отрезка [ a, b], на котором отделен корень данного уравнения, построим график функции y=65-lnx-x.

Откроем окно редактора системы Scilab SciPad командой scipad(); (или выполнив пункт меню Editor, или нажав пиктограмму с изображением чистого листа)и наберем в нем следующие строки:

clc

xbasc()

function y=f(x)

// определение функции, входящей в уравнение

y= 65-log(x)-x;

endfunction

x=50:0.1:70; plot(x, f(x)); xgrid()

После запуска программы (Execute/Load into Scilab) откроется графическое окно системы (Scilab Graphic(0)) с графиком функции y=65 – ln x – x на отрезке [50, 70], из которого видно, что корень нашего уравнения лежит на отрезке [60, 70]. Для уточнения значения корня наберем в командном окне системы Scilab строку

-->x0=60;x1= fsolve(x0,f)

и нажмем Enter. В итоге в командном окне появится искомый результат

x1 =

60.890916

Ответ: x = 60.8909

Содержимое окна редактора и командного окна системы Scilab необходимо переписать в тетрадь.

ЗАДАНИЕ 2

Методом наименьших квадратов (МНК) получить формулу аппроксимирующей параболы 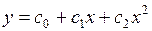для следующей таблицы:

а)

x m+n m+n+2 m+n+4 m+n+6 m+n+8

y g+q+2.5 g+q+4.9 g+q+8 g+q+12.1 g+q+16.9

Это же задание выполнить с использованием ИС Eureka и Scilab.

Пример выполнения задания 2: (вариант b, номер студента N_ст=50, g=0, q=0.)

x

y=f (x) 2.5 4.9 12.1 16.9

Аппроксимация – это замена одной функции у = f (x) (в нашем случае – приведенной выше табличной функции) другой функцией (в нашем случае – полиномом второй степени 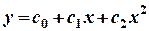). В методе наименьших квадратов коэффициенты с ₀, с ₁ и с ₂ подбирают так, чтобы величина

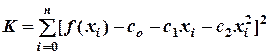
принимала минимальное значение. Здесь n – номер последнего узла таблицы. Нумерация ведется с нуля, то есть для нашей таблицы x ₀ = 5, x ₁ = 7, …, x ₄ = 13, n= 4.

Эта задача сводится к решению системы нормальных уравнений для определения неизвестных коэффициентов. В нашем случае три неизвестных коэффициента, надо решить систему из трех линейных уравнений:

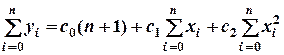
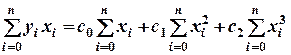
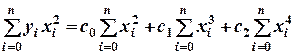
Составим вспомогательную таблицу:

i x_i y_i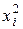

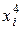
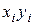
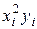
2.5 12.5 62.5

4.9 34.3 240.1

12.1 133.1 1464.1

16.9 219.7 2856.1

S 44.4 471.6 5270.8

Таким образом, для наших исходных данных имеем систему

44.4 = 5 c ₀ + 45 c ₁ + 445 c ₂

471.6 = 45 c ₀ + 445 c ₁ + 4725 c ₂

5270.8 = 445 c ₀ + 4725 c ₁ + 52789 c ₂,

решая которую (например, методом Гаусса), получаем:

с ₀= 0.24071429, с ₁= – 0.064285714, с ₂= 0.10357143.

Следовательно, нашу таблично заданную функцию мы заменили параболой y = 0.241 – 0.064 x +0.104 x ².

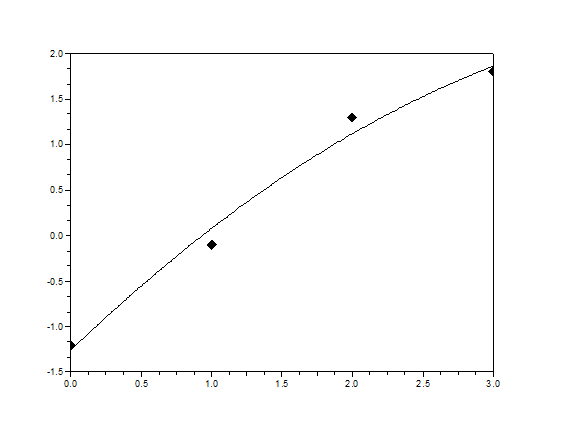
Последний этап решения: наносим исходные данные на координатную плоскость и на этой же плоскости строим полученную параболу.

Ответ: y = 0.241 – 0.064 x +0.104 x ²

Чтобы решить задачу с помощью ИС Eureka, в окне Edit надо набрать:

y (x): = c 0 + c 1 *x + c 2 *x^{^} 2

y (5) = 2.5

y (7) = 4.9

y (9) = 8

y (11) = 12.1

y (13) = 16.9

$ substlevel = 0

После выполнения команды Solve в окне Solution получим решение:

с 0 = 0.241

c 1 = – 0.064

c 2 = 0.104

Maximum error is 0.0511428571

Ответ: y = 0.241 – 0.064 x +0.104 x ²

Примечание: Если в каком-либо окне видны не все данные, то это окно можно распахнуть на весь экран, нажав клавишу F5.

Чтобы решить данную задачу с помощью ИС Scilab, можно в окне редактора системы набрать следующую программу:

xbasc()

clc

//Функция, вычисляющая разность между экспериментальными

//и теоретическими значениями,

//перед использованием необходимо определить

//z=[x;y] - матрицу исходных данных и

//с - вектор начальных значений коэффициентов,

//размерность вектора должна совпадать

//с количеством искомых коэффициентов

function y=G(c,z)

y=z(2)-c(1)-c(2)*z(1)-c(3)*z(1)^2

endfunction

//Исходные данные

x=[5 7 9 11 13];

y=[2.5 4.9 8 12.1 16.9];

//Формирование матрицы исходных данных

z=[x;y];//та же буква, что и в функции y=G(c,z)

//Вектор начальных приближений

c=[0;0;0];//нулей столько, сколько искомых коэффициентов. Это нач. приближение

//Решение задачи

[a,err]=datafit(G,z,c)

//Построение графика экспериментальных данных

plot2d(x,y,-4);

//Построение графика подобранной функции на отрезке [4, 14]

t=4:0.01:14;

Ptc=a(1)+a(2)*t+a(3)*t^2;

plot2d(t,Ptc);

После запуска программы (Execute/Load into Scilab) в командном окне получим:

err =

0.0051429

a =

0.2406191

- 0.0642614

0.1035701

Здесь err - сумма площадей квадратов отклонений, а – вектор искомых коэффициентов с₀, с₁и с₂.

Ответ: y = 0.1036 x ²– 0.0643 x + 0.2407

Очевидно, что коэффициенты с ₀, с ₁ и с ₂, полученные в результате решения непосредственно системы уравнений и с помощью ИС Eureka и Scilab, должны совпадать (с учетом погрешностей округления, которые мы делали, решая систему вручную).

ЗАДАНИЕ 3

По таблице из задания 2 вычислить значение функции в точке x ^* = m+n+ N_ст/30

a) с помощью интерполяционного полинома Лагранжа, используя первые три точки таблицы;

b) с помощью интерполяционного полинома Ньютона, используя все точки таблицы.

Это же задание выполнить с использованием ИС Eureka и Scilab.

Пример выполнения задания 4: (вариант а, N_ст= 51, g = 0,q = 0 .)

Интерполяция – это частный случай аппроксимации, когда аппроксимирующая кривая проходит через все или через часть точек таблицы.

Поскольку шаг в данной таблице – постоянный (h_i = x_i ₊₁– x_i = h = const), то для решения задачи интерполяции можно использовать как интерполяционный полином Лагранжа, так и интерполяционный полином Ньютона.

Для наших исходных данных получаем таблицу:

x

y 2.5 4.9 12.1 16.9

Покажем, как по первым трем точкам (узлам) таблицы построить интерполяционный полином Лагранжа. Степень интерполяционного полинома в данном случае будет равна двум (на единицу меньше числа узлов таблицы).

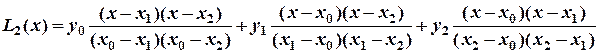(1)

Подставляя наши исходные данные в формулу (1), получаем:

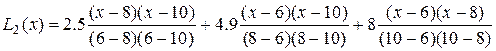
Здесь x ₀ = 6, x ₁ = 8, x ₂ = 10, y ₀ = 2.5, y ₁ = 4.9, y ₂ = 8.

Раскрыв скобки и приведя подобные члены, получим:

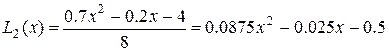
Проверим, проходит ли наш полином через три заданные точки таблицы:

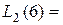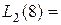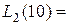0.0875ž6²– 0.025ž6 –0.5 = 2.5, 4.9, 8.

Подставляя теперь в этот полином вместо x число x^* = 6 + 51/30 = 7.7, получим:

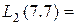0.0875ž7.7²– 0.025ž7.7 – 0.5» 4.495

Ответ:,» 4.495

Для решения задачи с помощью ИС Eureka в окне Edit набираем строки:

y (x) = c 0 + c 1 *x + c 2 *x^ 2

y (6) = 2.5

y (8) = 4.9

y( 10) = 8

t = y( 6 + 51/30)

После выполнения команды Solve в окне Solution получаем:

c 0 = – 0.5

c 1 = – 0.025

c 2 = 0.0875

t = 4.495375

Maximum error is 4.4408921e-16

Ответ:,» 4.495

Для построения полинома четвертой степени, проходящего через пять точек таблицы, воспользуемся формулой первого интерполяционного полинома Ньютона:

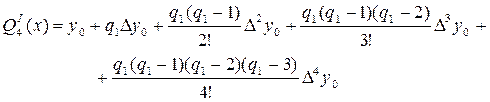(2)

Здесь 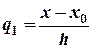, n! = 1ž2ž3ž4ž …žn. (Например, 5!=1ž2ž3ž4ž5=120).

Построим следующую таблицу конечных разностей:

i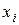

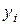
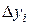
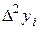
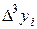
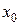
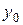
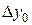
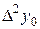
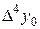
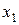
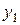
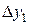
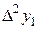
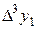
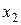
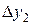
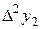
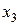
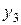
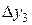
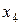
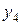
Здесь = – , = – , = – , = – , = – ,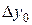

= – , = – , = – , = – ,

= – .

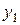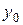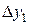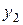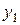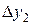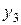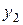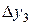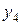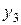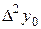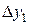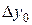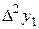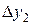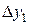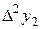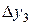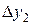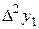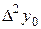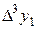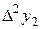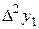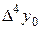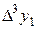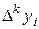– - это k -я конечная разность (k = 1, 2, 3, 4). В нашем примере

i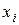

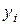
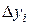
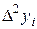
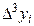
2.5 2.4 0.7 0.3 – 0.6

4.9 3.1 – 0.3

4.1 0.7

12.1 4.8

16.9

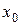= 6, 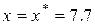(заданная точка), 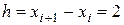. Тогда .

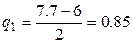Подставляя исходные данные в формулу (2), получим:

+

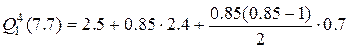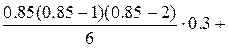
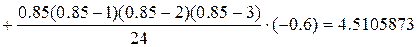
Ответ: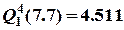

Чтобы решить эту же задачу с помощью ИС Eureka, в окне Edit набираем строки:

y (x): = c 0+ c 1* x + c 2* x ^2 + c 3* x ^3 + c 4* x ^4

y (6)=2.5

y (8)=4.9

y (10)=8

y (12)=12.1

y (14)=16.9

t = y (6+51/30)

После выполнения команды Solve в окне Solution получим:

c 0= –12.5

c 1= 5.425

c 2 = –0.80625

c 3= 0.625

c 4 = –0.015625

t = 4.5105873

Maximum error is 3.0198066e-14

Ответ: 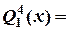– 12.5 + 5.425 x – 0.8063 x ²+ 0.625 x ³ – 0.0156 x ⁴,

t =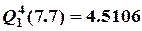

(Значения коэффициентов округлены до четырех знаков после запятой).

Чтобы решить вторую часть задачи (пункт b) с помощью ИС Scilab, можно воспользоваться программой

clc

xbasc()

x=[6 8 10 12 14];y=[2.5 4.9 8 12.1 16.9 ];nst=51;

n=length(x);a=[];b=[];c=[];

for i=1:n

for j=1:n

a(i,j)=sum(x.^(i+j-2));

end

b(i)=sum(x.^(i-1).*y);

end

c=inv(a)*b

function z=f(t)

z=0;

for i=1:n

z=z+t.^(i-1).*c(i);

end

endfunction

plot2d(x,y,-4)

t=min(x)-.1:.01:max(x)+.1;plot2d(t,f(t))

r=min(x)+nst/30,z1=f(r),plot(r,z1,"*")

err=sum((y-f(x)).^2)

Набрав эту программу в окне редактора и запустив ее на выполнение, в командном окне получим:

c = - 12.5 5.425 - 0.80625 0.0625 - 0.0015625

r = 7.7 z1 = 4.5105873 err = 6.351D-16

Коэффициенты интерполяционного полинома с даны в порядке возрастания степеней; r – точка, в которой необходимо вычислить значение функции (z1), err – сумма площадей квадратов отклонений (0 в задаче интерполяции). В графическом окне строится график интерполинома.

Ответ: ,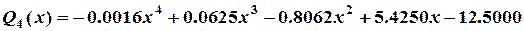

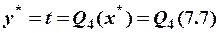» 4.5106

Для решения первой части задачи (пункт а) третья строка должна выглядеть так:

x=[6 8 10 ];y=[2.5 4.9 8 ];nst=51;

Ответы:

c = - 0.5 - 0.025 0.0875 r = 7.7 z1 = 4.495375 err = 3.564D-23

Ответ: ,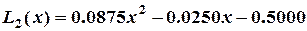

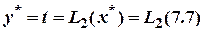» 4.4954

ЗАДАНИЕ 4

С помощью ИС Eureka и Scilab вычислить определенный интеграл

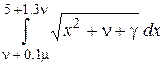
Тот же интеграл вычислить по обобщенным формулам левых прямоугольников, правых прямоугольников, трапеций и Симпсона, взяв шаг интегрирования равным одной десятой длины интервала интегрирования.

Пример выполнения задания 4: (вариант а, N_ст= 50, т.е. m= 5, n= 0.)

Вычислить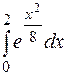

Численное интегрирование – это вычисление определенного интеграла от функции, заданной в виде таблицы. Для того, чтобы вычислить определенный интеграл по обобщенным формулам численного интегрирования, нужно привести подынтегральную функцию к табличному виду, т.е. составить таблицу ее значений на отрезке [ a, b ] с заданным шагом. В нашем задании шаг интегрирования .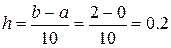

Таблица 1

x 0.2 0.4 0.6 0.8 1.2 1.4 1.6 1.8

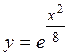
1.005 1.020 1.046 1.083 1.133 1.197 1.277 1.377 1.499 1.649

Здесь
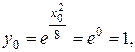
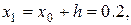
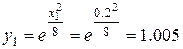
и т. д. (в числах оставлены три знака после запятой).

Обобщенная формула левых прямоугольников имеет вид:

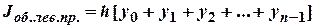
Здесь n –1 – номер предпоследнего узла таблицы.

Подставляя в формулу данные из таблицы 1, получим:

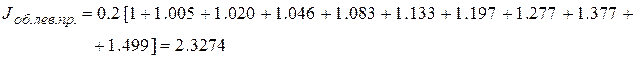
Обобщенная формула правых прямоугольников имеет вид:

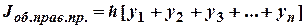
Здесь n – номер последнего узла таблицы.

Подставляя в формулу данные из таблицы 1, получим:

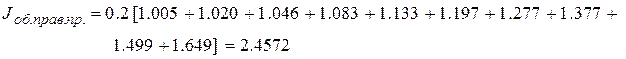
Обобщенная формула трапеций:

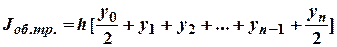
Подставляя в нее данные из таблицы 1, получим:

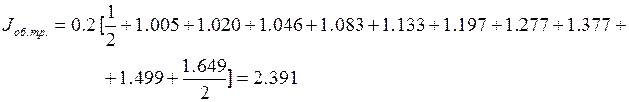
Обобщенная формула Симпсона (парабол):

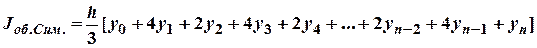
Подставляя в формулу данные из таблицы 1, получим:

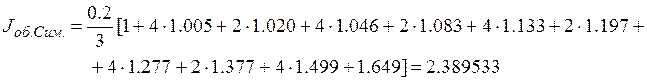
Ответ: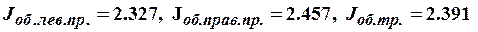

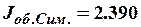
Решение задачи с помощью ИС Eureka:

В окне Edit набираем:

J = integ (exp (x ^2/8), x, 0, 2)

В окне Solution после выполнения команды Solve получим:

J = 2.3899153

Ответ: J =2.3899153

Примечание: exp(x ^2/8 ) – подынтегральная функция, x – переменная интегрирования, 0 – нижний предел интегрирования, 2 – верхний предел интегрирования.

Решение задачи с помощью ИС Scilab:

clc

function t=podint(x)

// определение подынтегральной функции

t=exp(x.^2/8);

endfunction

J=integrate('podint','x',0,2)

Примечание: точка после переменной x в выражении exp(x. ^2/8 ) необходима для перехода к поэлементной операции возведения в степень (см. с. 26).

После запуска набранного файла на выполнение (Execute/Load into Scilab) в командном окне появится результат

J = 2.3899153

Ответ: J =2.3899153