Задать в математическом пакете MatLab значения коэффициентов в соответствии с заданиями по вариантам, а также выражения для полиномов числителя и знаменателя каждого из рассмотренных типовых звеньев: пропорционального, интегрирующего, апериодического звена 1-го порядка, реального дифференцирующего и колебательного.
Затем сформировать передаточные функции каждого из типовых звеньев командой tf. Искомые характеристики систем могут быть найдены следующими командами MatLab
нахождение реакции системы на единичное ступенчатое воздействие.
step(W)
нахождение реакции системы на единичное импульсное входное воздействие;
impulse(W)
Амплитудно-фазовую характеристику системы в полярных координатах можно получить воспользовавшись командой
nyquist(W)
Логарифмическую амплитудно-фазовую характеристику системы в полярных координатах можно получить воспользовавшись командой
bode(W)
Расчет полюсов системы производится в командном окне при помощи команды
pole(W)
Расчет нулей системы производится в командном окне при помощи команды
zero(W)
Все указанные характеристики можно построить командой ltiview.
Например, для колебательного звена:
k=1;
T=1;
xi=0.5;
B5=[k];
A5=[T^2,2*T*xi,1];
W5=tf(B5,A5);
ltiview({'step';'impulse';'bode';'nyquist';'pzmap'},W5);
После построения графиков необходимо щелчком мыши на диаграмме Найквиста вызвать контекстное меню и отключить пункт меню Show→Negative Frequencies.
Для сохранения полученных характеристик необходимо сначала преобразовать их в рисунок, для этого выбрать пункт меню File→Print to Figure, затем скопировать его в отчет из меню Edit→Copy Figure, после чего вставить в файл с отчетом.
Далее необходимо произвести исследование влияния значений коэффициентов колебательного звена на его характеристики. Для этого необходимо сформировать новые передаточные функции.
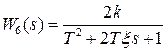для исследования влияния значения коэффициента усиления (увеличение коэффициента усиления вдвое).
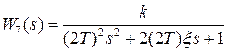для исследования влияния значения постоянной времени (увеличение коэффициента вдвое).
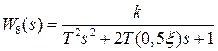для исследования влияния значения коэффициента демпфирования (уменьшение коэффициента в два раза).
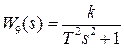– консервативное звено (коэффициент демпфирования 
).
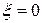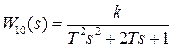– апериодическое звено второго порядка (коэффициент демпфирования 
).
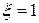Построить их типовые характеристики командой ltiview, при этом выводить характеристики базового колебательного звена. На одном графике производить не более одной модификации звена. Например, для консервативного звена
B9=[k];
A9=[T^2,0,1];
W9=tf(B9,A9);
ltiview({'step';'impulse';'bode';'nyquist';'pzmap'},W5,W9);
После построения последнего графика необходимо настроить вывод графика переходной характеристики. Для этого открыть меню Edit→Viewer Preferences, выбрать вкладку Parameters, после чего настроить значение в поле Time Vector→Define stop time до такого значения, чтобы график переходной характеристики консервативного звена совершал 3-4 колебания.
Исходные данные
Исходные данные по вариантам представлены в таблице 2.1.
Таблица 2.1
Параметры динамических звеньев
| Варианты | ||||||||||
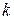
| 0,5 | 0,5 | ||||||||
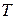
| 0,5 | 0,2 | 1,5 | 2,5 | 3,5 | |||||
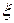
| 0,6 | 0,2 | 0,4 | 0,5 | 0,4 | 0,3 | 0,4 | 0,6 | 0,2 | 0,5 |
| Варианты | ||||||||||
|
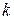
| 1,5 | |||||||||
|
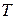
| 0,8 | 0,5 | 1,5 | 2,5 | ||||||
|
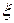
| 0,4 | 0,3 | 0,5 | 0,6 | 0,5 | 0,3 | 0,2 | 0,4 | 0,6 | 0,5 |
| Варианты | ||||||||||
|
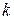
| 0,5 | 1,5 | 0,5 | |||||||
|
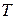
| 1,5 | 3,5 | 2,5 | 3,5 | 0,5 | |||||
|
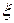
| 0,5 | 0,6 | 0,3 | 0,4 | 0,5 | 0,3 | 0,4 | 0,6 | 0,5 | 0,5 |
Порядок выполнения работы
2.5.1. Параметры звеньев установить в соответствии с вариантом задания (см. табл. 2.1.).
2.5.2. Осуществить моделирование и сохранить временные и частотные характеристики всех типовых динамических звеньев от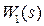 
до 
.
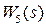2.5.3. Произвести моделирование базового варианта колебательного звена с его модификациями от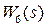 
до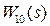 
, сохранить результаты в отчет.
2.5.4. Сделать выводы о влиянии того или иного параметра на характеристики колебательного звена.
2.5.5. Сделать сравнительный анализ результатов моделирования.
2.5.6. Оформить отчет в соответствии с 2.6.
2.5.7. Подготовиться к защите лабораторной работы, для чего ответить на вопросы для самоконтроля 2.7 и разобрать соответствующие разделы, изученные на лекциях и семинарских занятиях.
Содержание отчета
Отчет должен содержать следующие разделы:
2.6.1. Титульный лист установленного образца, содержащий номер и название лабораторной работы, Ф.И.О. автора, учебную группу, Ф.И.О. и должность преподавателя, номер варианта, место и год выполнения работы
2.6.2. Цель работы.
2.6.3. Исходные данные в соответствии с вариантом задания.
2.6.4. Математические модели типовых звеньев.
2.6.5. Результаты моделирования типовых звеньев.
2.6.6. Исследование влияния параметров колебательного звена на его характеристики.
2.6.7. Выводы.
Вопросы для самоконтроля
2.7.1. Назовите типовое динамическое звено, у которого корни знаменателя передаточной функции чисто мнимые, а числитель передаточной функции вещественная постоянная величина?
2.7.2. Какому динамическому звену соответствует переходная функция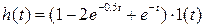 
.
Определить параметры этого звена.
2.7.3. Динамическое звено описывается дифференциальным уравнением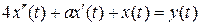 
. Найти значение параметра 
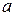, при котором звено будет колебательным.
2.7.4. Динамическое звено описывается дифференциальным уравнением 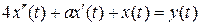. Найти значение параметра 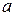, при котором звено будет апериодическим звеном второго порядка.
2.7.5. Определить переходную функцию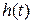 
динамического звена, заданного уравнением: 
.
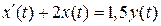2.7.6. Как влияет коэффициент усиления на временные характеристики системы?
2.7.7. Как влияет постоянная времени колебательного звена на временные характеристики системы?
2.7.8. Чем вызвано наличие пика на графике АЧХ консервативного звена?
2.7.9. Почему на диаграмме нулей и полюсов колебательного звена отмечены только полюса системы? А где же нули системы?
2.7.10. График какой функции изображен на диаграмме Найквиста?
2.7.11. Как между собой связаны графики переходной характеристики и импульсной переходной функции? Как это проверить?
2.7.12. Почему на практике не используется идеальное дифференцирующее звено?
