Процессы преобразования энергии в ней

 

Турбинная ступень осевого типа (рис. 4.1) состоит из неподвижной диафрагмы 1 с кольцевой решеткой сопловых лопаток2 и вращающегося диска5 с решеткой рабочих лопаток 4. Профили соответствующих лопаток и межлопаточные каналы решеток показаны на развертке цилиндрического сечения по среднему диаметру d _ср ступени. Диафрагма устанавливается в расточке корпуса или обоймы 3, а диск является элементом ротора 6. Уплотнение 7 кольцевой щели между диафрагмой и поверхностью ротора называют диафрагменным. В свою очередь уплотнение 8 периферийного зазора над рабочей решеткой называют надбандажным.

В сопловых каналах при расширении пара от давления р ₀ до давления р ₁ тепловая энергия преобразуется в кинетическую, в результате чего за сопловой решеткой среда приобретает скорость с ₁ (абсолютная скорость растет от с ₀ до с ₁), направление которой по отношению к фронту решетки определяется углом a ₁ (рис. 4.2). В межлопаточных каналахрабочей решетки при повороте потока и дальнейшем расширении пара до давления р ₂ ее кинетическая энергия преобразуется в механическую. При обтекании рабочих лопаток с криволинейным профилем (при повороте потока в каналах - рис. 4.2) создается активная составляющая усилия R_акт, а при расширении пара за счет ускорения потока – реактивная R_реак,которые формируют окружное усилие: .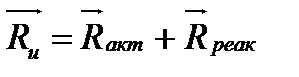

 

Рис. 4.1. Конструкция турбинной ступени (а) и ее упрощенное представление (б):

1 – диафрагма; 2 – сопловая решетка; 3 – обойма; 4 – рабочая решетка; 5 – диск; 6 – фрагмент ротора;

7 – диафрагменное уплотнение; 8 – надбандажное уплотнение

 

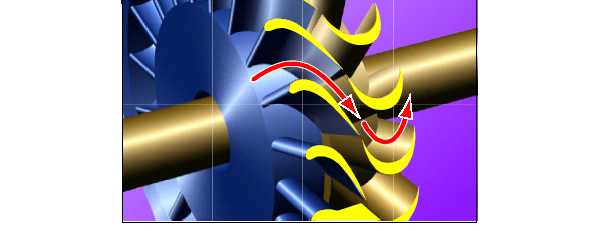
а)

б)

Рис. 4.2. Схема движения пара в турбинной ступени (а) и проточная часть каналов решеток двух последовательно установленных турбинных ступеней (б)

 

Визуализация течения в каналах сопловой и рабочей решеток турбинной ступени показана на рис. 4.3.

Рис. 4.3. Результаты визуализации течения рабочей среды в проточной части сопловой (а) и рабочей (б) решеток турбинной ступени (плоская модель)

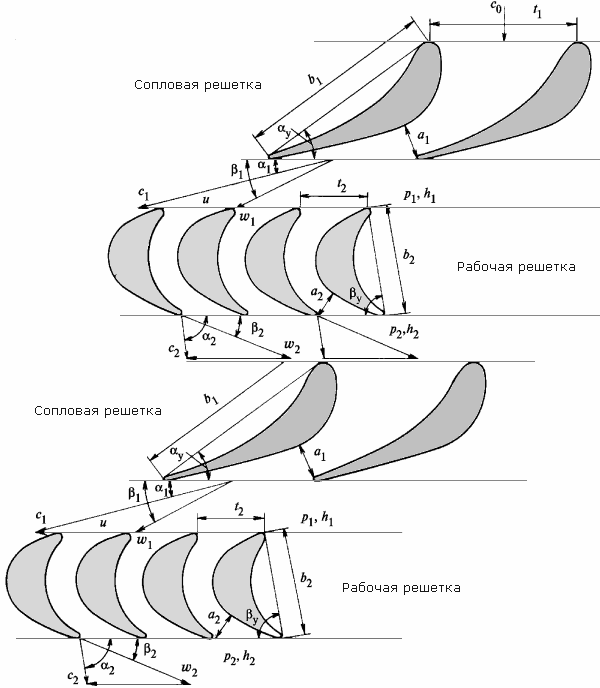
Окружное усилие R_u на соответствующем диаметре ступени формирует крутящий момент М _кр, который и производит работу по преодолению сил сопротивления приводимой машины (ротора электрического генератора). Рабочая решетка вращается с окружной скоростью u=pdn, где n, с^-1 - частота вращения ротора. В этой связи на входе в каналы рабочей решетки рассматривается движение пара с относительной скоростью w ₁ (относительно фронта решетки). Вектор скорости w ₁ определяется на основе входного треугольника скоростей: 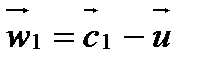(рис. 4.4). Угол между векторами относительной и окружной скоростями обозначают b ₁. Этим углом определяется направление входных кромок рабочих лопаток. На выходе из каналов рабочей решетки угол b ₂ относительной скорости w₂ определяется формой профиля рабочих лопаток и их установкой относительно ротора турбины. Абсолютная скорость с ₂ находится на основе выходного треугольника скоростей: (рис. 4.4). Угол вектора скорости с ₂ по отношению к фронту рабочей решетки обозначают a ₂. Обычно входной и выходной треугольники скоростей совмещают в их вершинах (рис. 4.4) и в таком виде они отражают кинематику процесса расширения рабочей среды в проточной части турбинной ступени. Представленные треугольники скоростей служат основой для расчета ее геометрических и аэродинамических характеристик. При этом углы b ₂ и a ₂ отсчитывают по часовой стрелке.

Рис. 4.4. Треугольники скоростей для турбинной ступени осевого типа:

входной треугольник: С₁ – абсолютная скорость потока на выходе из сопловой решетки;

W₁ – относительная скорость входа потока в рабочую решетку;

U – окружная составляющая скорости (U=pdn);

выходной треугольник: С₂ – абсолютная скорость потока на выходе из рабочей решетки;

W₂ – относительная скорость выхода потока из рабочей решетки

 

4.3. Тепловая диаграмма процесса расширения в турбинной ступени

 

Процессы расширения водяного пара в сопловой и рабочей решетках турбинной ступени представлены тепловой диаграммой в h-s координатах на рис. 4.5. Состояние пара перед ступенью по параметрам торможения 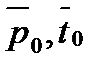определяется энтальпией (рис. 4.5, а). В свою очередь, значения статического давления р ₀ и температуры t ₀, позволяют определить теплосодержание среды энтальпией h₀. При расширении пара до давления р ₁ (линия 0 - 1 t) теплоперепад в условиях изоэнтропийного течения называют располагаемой энергией сопловой решетки. Она равна сумме кинетической энергии на выходе из сопловых каналов 0,5 с _{1 t} ² (в условиях изоэнтропийного расширения) и кинетической энергии на входе в них 0,5с₀². На основе уравнения сохранения 0,5 с ₀ ² + h ₀ = 0,5 c _{1 t}² + h _{1 t} теоретическое значение скорости истечения пара из сопловых каналов определяется выражением:

(4.8)

Действительная скорость из-за потерь энергии в сопловой решетке определяется выражением с ₁ = j с _{1 t}, где коэффициент скоростиj является оценкой коэффициента потерь сопловой решетки

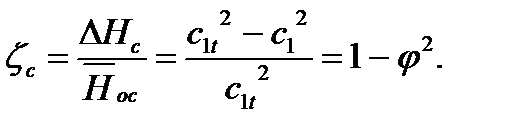(4.9)

Потери энергии D Н_с в сопловой решетке определяют необратимость процесса расширения в ней и соответствующее повышение энтальпии в реальном процессе (линия 0-1 на рис. 4.5, а) до значения h ₁ = h _{1 t} + D Н_с. В первом приближении коэффициент скорости для сопловой решетки допускается определять по выражению

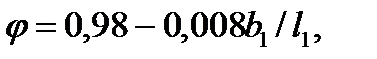(4.10)

где b₁ – хорда профиля сопловой лопатки (наименьшее расстояние между ее входной и выходной кромками, см. рис.4.2), l₁ – высота сопловой решетки. Тогда

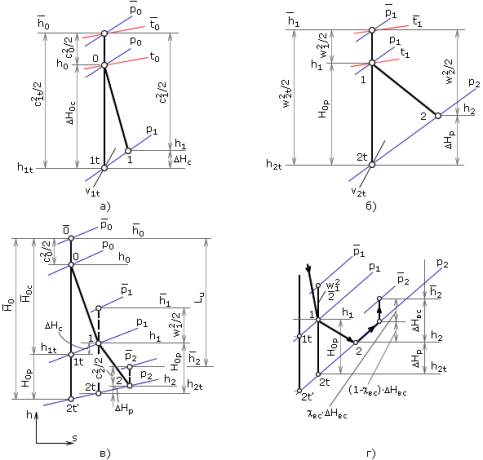
Рис. 4.5. Процессы расширения пара в каналах сопловой решетки (а), рабочей решетки (б) и в целом для турбинной ступени (в) (фрагмент процесса за ступенью с учетом степени использования энергии с выходной скоростью показан позицией г))

 

Теоретический (изоэнтропийный) процесс расширения пара в рабочей решетке ступени до давления р ₂ представлен на рис. 4.5, б линией 1-2 t. Разность энтальпий h ₁ - h _{2 t} = H_op называют располагаемым теплоперепадом рабочей решетки по статическим параметрам, а уравнение энергии для нее в относительном движении имеет вид: h ₁ + 0,5 w ₁ ² = h _{2 t} + 0,5 w _{2 t}² (при условии равенства средних диаметров входного и выходного сечений рабочей решетки). В правой части этого уравнения отсутствует составляющая, характеризующая отводимую от рабочей решетки механическую работу посредством диска к ротору турбины. Следует понимать и помнить, что эта работа, формируемая силой взаимодействия между рабочей лопаткой и потоком в координатах вращающейся решетки турбинной ступени равна нулю, так как точка приложения этой силы не перемещается по отношению к наблюдателю, условно вращающемуся вместе с решеткой. Тогда теоретическая скорость в относительном движении на выходе из каналов рабочей решетки

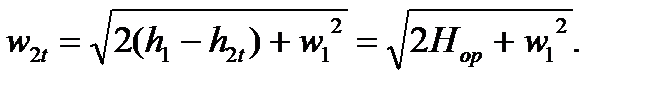(4.11)

Действительная скорость с учетом коэффициента скорости для рабочей решетки y равна w ₂ = yw _{2 t}. Как и для сопловой коэффициент потерь рабочей решетки

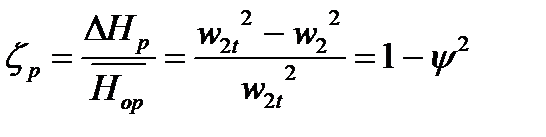, (4.12)

где 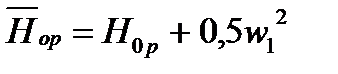- располагаемая энергия рабочей решетки, определяемая по параметрам торможения среды на входе в относительном движении (по давлению 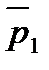). Потери энергии в каналах рабочей решетки , где в первом приближении коэффициент скорости допускается определять по выражению

y=0,96-0,014b₂/l₂, (4.13)

где b₂ – хорда профиля рабочей лопатки (наименьшее расстояние между ее входной и выходной кромками, см. рис.4.2), l₂ – высота рабочей лопатки.

Тогда для реального процесса расширения (линия 1-2 на рис. 4.5, б) энтальпия пара в выходном сечении рабочей решетки h ₂ = h _{2 t} + D H_р.

Разность энтальпий h ₀ - h _{2 t'} = Н₀ называют располагаемым теплоперепадом ступени по статическим параметрам ( рис.4.5,в ), а теплоперепад, включающий кинетическую энергию потока на входе в ступень 0,5 с ₀ ², располагаемым теплоперепадом по параметрам торможения на входе в ступень: 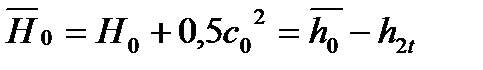' ( рис. 4.5, в).Сумма располагаемых теплоперепадов сопловой и рабочей решеток называется располагаемой энергией ступени: 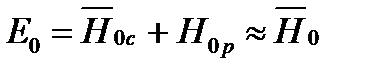. Эта энергия выражает работу, которую теоретически можно получить от 1 кг водяного пара в турбинной ступени.

На выходе из рабочей решетки поток пара обладает кинетической энергией D Н _вс = 0,5 с ₂ ², определяемой абсолютной скоростью с ₂. В практике D Н _вс называют потерей энергии с выходной скоростью. В зависимости от степени использования D Н _вс в последующей ступени соответствующий процесс в h,s -диаграмме изображается или изобарным, или изоэнтропийным (рис.4.5,в), или совмещенным (рис. 4.5, г). Если рабочая среда после ступени попадает в относительно емкую камеру проточной части (например, за регулирующей ступенью или за последними ступенями цилиндров турбины), то вся энергия с выходной скоростью расходуется на повышение температуры вследствие изобарного торможения среды. Такой процесс оценивается значением коэффициента использования энергии выходной скоростиc _вс =0, а располагаемая энергия ступени в этом случае

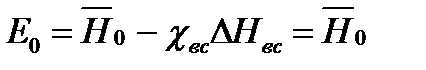. (4.14)

Для промежуточной ступени цилиндра турбины энергия выходной скорости используется в последующей ступени и определяет рост располагаемой энергии последующей ступени (0< c _вс£1). Тогда, например, при c _вс=1 для рассматриваемой ступени . На рис. 4.5, г приведено изображение процесса для случая, когда значение коэффициента 0 <c_вс<1. При этом доля (1- c _вс)D Н _вс кинетической энергии с выходной скоростью теряется полностью, а другая часть c_всD Н _вс используется в последующей ступени для совершения механической работы. Эта часть для нее составляет энергию входной скорости 0,5 с₀ ².

Из рассмотренного процесса расширения рабочей среды в проточной части турбинной ступени (рис. 4.5, в) следует выражение для удельной (для 1 кг пара) работы ступени L_u. Удельная работа на лопатках рабочей решетки

(4.15)