Исходные данные
Требуется построить полиномиальные модели различных степеней вида
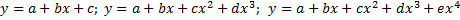
и сравнить оценки их погрешностей. Определение коэффициентов таких уравнений осуществить средством Поиск решения.
Табл.2.
| x | ||||||||||
| у (значение наблюдаемой величины) |
Порядок выполнения работы
Ø Подготовим начальный рабочий лист кА показано на рис.7. Заданные ряды Y и t помещены в диапазоны С7:С16 и А7:А16 соответственно. В диапазонах С7:С16, D7:D16, E7:E16 будем отображать квадраты погрешности между фактическим значением Yi и полученным из полиномов второй, третьей и четвертой степени уравнений регрессии соответственно.
Рис.7.
Ø Введем следующие формулы:
С7 =($B7-($B$3+$C$3*$A7+$D$3*$A7^2))^2 (12)
D7=($B7-($B$4+$C$4*$A7+$D$4*$A7^2+$E$4*$A7^3))^2 (13)
E7=($B7-($B$5+$C$5*$A7+$D$5*$A7^2+$E$5*$A7^3+$F$5*$A7^4))^2 (14)
Ø Cкопируем эти формулы в диапазон С8:С16, D8:D16, E8:E16 соответственно. Полученные результаты сравним между собой ряды квадратов погрешностей полиномов.
Ø В ячейке С17 вычислим сумму квадратов погрешностей для приближения полиномом 2-й степени, введя формулу:
С17 = СУММ (С7:С16) (15)
Скопируем эту формулу методом буксировки вправо на диапазон D17:Е17, чтобы вычислить сумму квадратов погрешностей приближений полиномами 3-й и 4-й степени. Сравним результаты в ячейках С17:Е17 между собой.
Ø Для вычисления коэффициентов а, b, c полинома второй степени выберем команду Сервис/Поиск решения. В диалоговом окне Сервис/Поиск решения установим целевую ячейку С17, в поле Равной установим минимальному значению, в поле Изменяя ячейки – диапазон B3:D3. После щелчка Выполнить, результаты поиска – значения коэффициентов а, b, с появляются в ячейках B3:D3.
Ø Аналогично предыдущему пункту, используя средство Поиск решения, определим коэффициенты а, b, c, d в ячейках В4:Е4 для приближения полиномом 3-й степени, затем то же самое для приближения полиномом 4-й степени в ячейках В5:F5 определим коэффициенты а, b, c, d, e.
Ø Сделаем нелинейный регрессионный анализ, используя средства деловой графики Excel, не прибегая к вычислениям, сначала для модели 2-й степени. Для этого построим график Y(t), используя ряды t и Y в ячейках А7:А16, В7:В16. Затем кликнув щелчком на этом графике правой кнопкой мыши и в появившемся контекстном меню выберем пункт Добавить линию тренда. В появившемся окне Линия тренда, в котором выберем тип уравнения аппроксимации Полиномиальная и его степень; на вкладке Параметры установим флажки Показывать уравнение на диаграмме, Поместить на диаграмму величину достоверности аппроксимации. Будет выведен график уравнения регрессии и само уравнение с числовыми значениями коэффициентов и квадрат коэффициента корреляции R^2.
Ø Аналогично выполним графическое построение линий тренда для полиномов 3-й, 4-й степеней с показом уравнений на графике. Сравним регрессионные модели полиномами
Рис.8. Результаты решения
Выводы
В данной работе был изучен метод решения задач регрессионного анализа с применением средств Excel. Получены навыки использования команды Сервис/Подбор параметра, встроенных статистических функций для построения линейных и нелинейных уравнений регрессии и линий тренда.
С помощью команды Сервис/ Подбор параметра, функций НАКЛОН(), ОТРЕЗОК() и ЛИНЕЙН() разными способами рассчитаны значения а и b линейной регрессионной модели. Проведен сравнительный анализ полученных значений, значения …… … получились одинаковыми. По полученным данным построены диаграммы с линией тренда типа Линейная. Также получены теоретические значения yt при t с помощью функции ПРЕДСКАЗ() и новые значения у с помощью функции ТЕНДЕНЦИЯ().
Для определения параметров нелинейной экспоненциальной модели использовались формулы ЛГРФПРИБЛ, LN. Для построения экспоненциального тренда – функцию РОСТ. Вычислены теоретические значения yt (нелин) наблюдаемой величины, используя экспоненциальную модель и построена диаграмма с линией тренда типа Экспоненциальная.
Коэффициент корреляции в линейной и экспоненциальной модели различается на 0,0212 (R2лин > R2экс).
Во второй части данной работы построены полиномиальные модели различных степеней. Для этого были использованы формулы 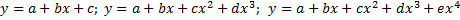. Для вычисления коэффициентов а, b, c полинома различных степеней использована команда Сервис/Поиск решения. По полученным данным построен график Excel для модели 2-й, 3-й, 4-й степени. Сравнивая оценки погрешностей полиномонов 2-й, 3-й, 4-й степеней можно сделать вывод, что погрешность уменьшается с увеличением степени, особенно это наглядно представлено из вычисленных сумм квадратов разностей.
