Киреев Б.Н.
Основы гидропривода. Гидравлические
И пневматические системы.
Методика решения типовых задач.
При решении многих проблем в самых разнообразных отраслях промышленности часто при-ходится встречаться с вопросом о движении различных жидкостей и газов, а также с вопросом о силовом (механическом) их воздействии на те или другие поверхности и на обтекаемые ею твер-дые тела.
Изучение законов движения жидкостей и газов привело к созданию различных гидро- и пневмоустройств, широко используемых в настоящее время на практике. Наибольшее распрос-транение получили гидравлические (гидронасосы, гидродвигатели) и пневматические (пнев-модвигатели) машины.
Расчёты проводятся с использованием единиц измерения системы СИ. В отдельных случа-ях используются внесистемные единицы. В большинстве задач решения снабжены рисунками и подробными пояснениями.
Цель:
- изучить методику решения задач по гидравлике, газодинамике, гидравлическим машинам, гидроприводу;
- использовать полученные знания для выполнения самостоятельной (контрольной) работы.
Задание 1. Прежде чем приступать к изучению методики решения задач, необходимо изучить лекционный материал по данной тематике.
Задание 2. Изучить методику решения типовых задач, используя приведенные ниже примеры
Задание 3. Использовать данную методику при выполнении самостоятельной и конт-рольной работы. Варианты работ и контрольные задания приведены ниже.
Основы гидравлики
Тема 1: «Физические свойства жидкостей»
Задача 1. Определить коэффициент динамической и кинематической вязкости воды, если шарик d = 2мм, из эбонита, плотность которого ρш = 1,2· 103  падает в воде с постоянной скоростьюu = 0,33
падает в воде с постоянной скоростьюu = 0,33  . Плотность воды ρж=103
. Плотность воды ρж=103  .
.
Решение.
При движении шарика в жидкости с постоянной скоро-стью результирующая сила, равная сумме трёх сил (силы сопро-тивления движению Fc, силы тяжести Fт и выталкивающей силы Fвыт) равняется нулю (согласно второму закону Ньютона Fрез= m•a=0, так как ускорение равно нулю). Fрез= Fт- Fвыт-Fс = m•a=0 (1) ОтсюдаFc= Fт- Fвыт (2)
Сила сопротивления определяется по формуле Стокса: Fc= 6π·r·η·u = 3π· d· η · u. (3) Вес шарика определяется по фор-муле: Fт=mg = ρш · V · g = ρш · ( ) · g. (4) Выталкивающая сила равна весу вытесненной жидкости: Fвыт= ρж · V · g = ρж · (
) · g. (4) Выталкивающая сила равна весу вытесненной жидкости: Fвыт= ρж · V · g = ρж · ( ) · g (5) Подставляем в формулу (2) значения сил из (3), (4) и (5), получаем:
) · g (5) Подставляем в формулу (2) значения сил из (3), (4) и (5), получаем:
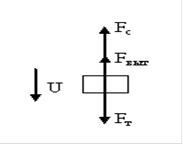
Рис. 1 к задаче 1.Схема сил, действующих на падающее равномерно тело в жидкости.
3π · d · η · u = ρш · ( ) · g – ρж · (
) · g – ρж · ( ) · g(6) Из формулы (6) находим значение динамической вязкости воды: η =
) · g(6) Из формулы (6) находим значение динамической вязкости воды: η =  =
= 
η =  = 1,32 · 10-3 Па · с. Коэффициент кинематической вязкости: χ =
= 1,32 · 10-3 Па · с. Коэффициент кинематической вязкости: χ =  =
=  =1,32 · 10-6
=1,32 · 10-6 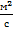 .
.
Ответ: коэффициент кинематической вязкости воды при комнатной температуре χ =1,32 · 10-6 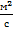 .
.
Задача 2. Определить избыточное давление на дне океана, глубина которого Н=10 км, приняв плотность морской воды ρ0 = 1025  и считая ее несжимаемой. Определить плот-ность воды на той же глубине с учетом сжимаемости и приняв модуль объемной упругости к=2020 МПа.
и считая ее несжимаемой. Определить плот-ность воды на той же глубине с учетом сжимаемости и приняв модуль объемной упругости к=2020 МПа.
Решение
Избыточное давление на глубине Н без учёта сжимаемости воды:
Р = ρgH= 1025  •9,8
•9,8  •104 м = 10,04 •107 Па = 100,4 МПа. Модуль объёмной упругости k = -
•104 м = 10,04 •107 Па = 100,4 МПа. Модуль объёмной упругости k = - 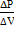 ∙ v. Сжимаемость жидкости: βр =
∙ v. Сжимаемость жидкости: βр =  = -
= -  ·
·  . Заменяя значения бесконечно малых изменений dV на значения конечных изменений объёма ∆V, находим значения сжимаемости: βр = 1/к = -
. Заменяя значения бесконечно малых изменений dV на значения конечных изменений объёма ∆V, находим значения сжимаемости: βр = 1/к = -  ·
· 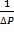 . βр =
. βр =  =
=  = 4,95 •10-10 (
= 4,95 •10-10 (  ). Конечное значение объёма V= V0·(1- βр·∆ p ). По определению удельного объёма υ =
). Конечное значение объёма V= V0·(1- βр·∆ p ). По определению удельного объёма υ =  . Следовательно, при давлении Р:
. Следовательно, при давлении Р:
ρ = 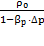 =
= 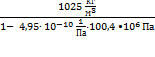 ;
;
ρ =  =1079
=1079 
Ответ: значения плотности морской воды на глубине 5 км ρ = 1079  .
.
Тема 2:«Основы гидростатики»
Задача 3. Определить показание мановакуумметра  , если к штоку поршня приложена сила F =0,5 кН, его диаметр d = 78 мм, высота H= 1,5 м, плотность жидкости
, если к штоку поршня приложена сила F =0,5 кН, его диаметр d = 78 мм, высота H= 1,5 м, плотность жидкости  = 800
= 800  .
.
Решение:
Гидростатическое давление в точке С (сверху) под слоем жидкости можно определить, используя закон Паскаля: Рс= Р0+ 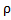 gH. Давление в воздухе над поверхностью жидкости Р0 = Ратм+ Рмв. Давление справа, со стороны поршня Рс=Ратм+
gH. Давление в воздухе над поверхностью жидкости Р0 = Ратм+ Рмв. Давление справа, со стороны поршня Рс=Ратм+  . Давление в жидкости в любой её точке одинаково со всех сторон.
. Давление в жидкости в любой её точке одинаково со всех сторон.

Рис. 2 к задаче 3.
Следовательно:Р0+  gH= Ратм+
gH= Ратм+  . Ратм+ Рмв +
. Ратм+ Рмв +  gH = Ратм+
gH = Ратм+  .
.
Отсюда находим Рмв=  -
-  gH.
gH.  =
=  –800
–800  9,8
9,8 
 =1,05
=1,05  105Па – 0,12
105Па – 0,12  105Па =0,93
105Па =0,93  105Па = 93 кПа.
105Па = 93 кПа.
Ответ: показания мановакуумметра Рмв= 93 кПа.
Задача 4. Определить манометрическое давление в центре трубопровода (точка А), если высота столба ртути по пьезометру h2 = 0,30 м. Центр трубопровода расположен на h1 = 0,5 м ниже линии раздела между водой и ртутью.
Решение:
Находим давление в точке В. Точка В расположена выше точки А на величину h1. Давление в точках В, С и D будут одина-ковы (в одной и той же жидкости на одинаковой высоте значения давлений одинаковы). Абсолютное давление в точке D (а, следовательно, и точке В) равно сумме давления столба ртути высотой h2 и атмосферного давления Ратм. Абсолютное давление в точке А равно сумме давления в точке В и давления столба воды высотой h1. Следовательно: РА= ρв gh1 + Ратм + ρрт gh2 ; Манометрическое
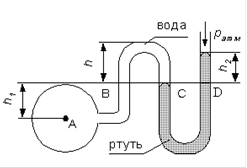
Рис.3к задаче 4.
давление (в данном случае это избыточное давление) равно раз-ности абсолютного и атмосферного давлений. Следовательно РАм= (103  • 0,5 м + 13,6 • 10 3
• 0,5 м + 13,6 • 10 3  • 0,30 м) • 9,8
• 0,30 м) • 9,8  = 44,9 • 103Па.
= 44,9 • 103Па.
Ответ: манометрическое (избыточное) давление в центре трубы РАм= 44,9 кПа.
Тема 3: «Основы гидродинамики»
Задача 5. Разность пьезометрических напоров в сечениях 1-1 и 2-2 равна 30 см. Определить коэффициент линейных потерь на участке между сечениями 1 и 2, если длина участка трубы L = 1 м, диаметр трубы d= 20 мм, а расход жидкости, протекающей по трубе Q =0,54  .
.
Решение:
Запишем уравнение Бернулли в общем виде для потока реальной жидкости:
[ 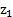 +
+  +
+ 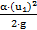 ]- [
]- [  +
+  +
+  ] = h1-2
] = h1-2

Рис. 4 к задаче 5.
Коэффициенты Кориолиса можно взять равными 1, так как о них в условиях задачи нет сведений. Определить их, используя число Рейнольдса, так же нельзя, так как не указана жидкость и нет данных по её плотности и вязкости. Условно принимаем движение жидкости турбулентным, что чаще всего и бывает на практике. Для такого вида движения коэффициенты Кориолиса равны 1. При равенстве диаметров сечений 1 и 2 средние скорости движения жидкости и скоростные напоры одинаковы. Их разность равна нулю. По определению, геометрические напоры также одинаковы. Их разность тоже равна нулю. С учётом сказанного уравнение Бернулли принимает вид:
(Hп1 - Hп2 ) = h1-2
Важный вывод: в горизонтальных трубах постоянного диаметра полные потери напора численно равны разности пьезометрических напоров в выбранных сечениях 1-1 и 2-2.
Так как на данном участке трубы местные сопротивления отсутствуют, полные потери равны линейным потерям напора. Согласно формуле Дарси:
hл = λтр · (  ) ·
) ·  Следовательно, в данном случае (Hп1 - Hп2 ) = λтр · (
Следовательно, в данном случае (Hп1 - Hп2 ) = λтр · (  ) · (
) · (  ). Отсюда находим коэффициент линейных потерь:
). Отсюда находим коэффициент линейных потерь:
λтр =  .
.
Скорость движения жидкости в трубе находим через расход жидкости:
U =  ; S =
; S = 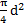 =
=  = 3,14 ·10-4 м2
= 3,14 ·10-4 м2
Подставляем значения и находим скорость:
U =  =
=  = 1,72
= 1,72  .
.
Находим коэффициент линейных потерь:
λтр =  =
=  = 0,04.
= 0,04.
Ответ: коэффициент линейных потерь на участке трубы составляет λ = 0,04.
Задача 6. В горизонтально расположенной трубе диаметром 6,0 см на расстоянии L = 10 м друг от друга расположены два манометра, между которыми находится кран, имеющий коэффициент местного сопротивления ε =2,7. Определить коэффициент линейных потерь на участке между сече-ниями 1 и 2, если разность показаний манометров равна 2,16 кПа, а расход жидкости в трубе составляет Q= 2  . Жидкость – вода, при 200С (плотность ρ = 103
. Жидкость – вода, при 200С (плотность ρ = 103  , а динамическая вяз-кость η=10-3 Па
, а динамическая вяз-кость η=10-3 Па  с.
с.
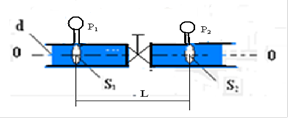
Рис.5 к задаче 6.
Решение:
Запишем уравнение Бернулли в общем виде для потока реальной жидкости:
[ 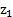 +
+  +
+ 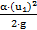 ]- [
]- [  +
+  +
+  ] = h1-2
] = h1-2
Коэффициенты Кoриолиса определим, рассчитывая число Рейнольдса. При Re>4000 (режим течения турбулентный) коэффициент Кориолиса равен 1, а при Re< 2300 (режим течения ламинарный) коэффициент Кориолиса равен 2. Находим число Рейнольдса: Re = 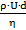 . Скорость течения воды:
. Скорость течения воды:
U=  =
=  =
=  = 0,71
= 0,71  .
.
Re = 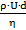 =
=  = 42600. Режим турбулентный, α = 1. При равенстве диаметров сечений 1 и 2 средние скорости движения жидкости и скоростные напоры одинаковы. Их разность равна нулю. По определению, геометрические напоры также одинаковы. Их разность также равна нулю. С учетом сказанного, уравнение Бернулли принимает вид:
= 42600. Режим турбулентный, α = 1. При равенстве диаметров сечений 1 и 2 средние скорости движения жидкости и скоростные напоры одинаковы. Их разность равна нулю. По определению, геометрические напоры также одинаковы. Их разность также равна нулю. С учетом сказанного, уравнение Бернулли принимает вид: 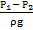 =
=  . Согласно Дарси:
. Согласно Дарси:  = λ · (
= λ · ( 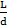 ) ·
) · 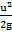 ;
;  ; Следовательно, в данном случае:
; Следовательно, в данном случае:
 = λ · (
= λ · ( 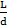 ) ·
) · 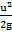 +
+  . Отсюда находим коэффициент линейных потерь:
. Отсюда находим коэффициент линейных потерь:
(Р1-Р2)= ρ  [λ
[λ  (
(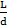 ) +
) +  ]; λ
]; λ  ) +
) +  =
=  ;
;
λ  ) =
) =  -
-  ;λ=
;λ=  =
=  ;
;  ) =
) = 
λ =  = 0,035.
= 0,035.
Примечание: если в условиях задачи задана разность пье-зометрических напоров Н ( м ), то коэффициент гидравлического трения удобнее рассчитывать как:
λтр = 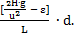
Ответ: коэффициент линейных потерь на участке трубы между сечениями 1 и 2 составляет λ = 0,035.
Задача 7. По трубе диаметром 5,06 см течёт вода со скоростью U = 1  . Принимая плотность жидкости равной ρ = 1
. Принимая плотность жидкости равной ρ = 1 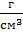 , а динамическую вязкость η = 0,001 Па·с, определить число Рейнольдса, а затем коэффициент линейных потерь.
, а динамическую вязкость η = 0,001 Па·с, определить число Рейнольдса, а затем коэффициент линейных потерь.
Решение:
Число Рейнольдса определяется следующим образом: Re = Red =  ;
;
Re = 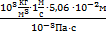 = 5,06 ·10 4 Получим размерность числа Рейнольдса:
= 5,06 ·10 4 Получим размерность числа Рейнольдса:
Па  с =
с = 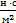 =
= 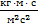 =
=  ;
;
 м =
м =  ;
; 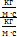 = 1. Число Рейнольдса не имеет размерности (безразмерное число).
= 1. Число Рейнольдса не имеет размерности (безразмерное число).
Число Рейнольдса оказалось больше критического. Для нахождения коэффициента Дарси (коэффициента линейных потерь) в интервале 4000 <Re< 105 используем формулу Блазиуса:
λтр =  =
=  =
=  = 0,02.
= 0,02.
Ответ: Re = 5,06 ·10 4; λ = 0,02.
Тема 4: «Основы газодинамики»
Основной отличительной особенностью движения газа по трубам от движения капельных жидкостей заключается в том, что капельные жидкости характеризуются малой сжимаемостью, а их вязкость практически не зависит от давления. По этой причине для решения большинства прак-тических задач капельные жидкости можно считать не сжимаемыми, что позволяет значительно упростить уравнения движения такой жидкости.
При движении газа таких допущений делать нельзя. Газ двигается по газопроводу при переменном давлении, т.к. давление изменяется вдоль длины газопровода из-за неизбежных по-терь напора по длине трубопровода. По этой причине плотность газа и его вязкость являются величинами переменными и неодинаковы в различных сечениях газопровода. Рассмотрим наибо-лее простой случай газопровода (воздуховода) – трубы одинакового диаметра (простой газопровод S = const) при установившемся движении газа. Тогда в соответствии с уравнением не-разрывности потока газа массовый расход газа вдоль газопровода является величиной постоянной  = const.При этом объёмный расход Qv газа будет меняться от одного сечения газопрово-да к другому, т.к. плотность газа зависит от давления, которое по длине газопровода меняется. При этом должна изменяться и температура газа по длине газопровода, и, как следствие, также и вязкость газа. Однако для решения практических задач движе-ние газа по трубопроводу можно считать изотермическим (небольшие скорости движения, теплоизоляция газопровода, небольшие перепады давления). Это допущение не приведет к серьёзным погрешностям в расчётах, но оно позволяет пренебречь изменением вязкости газа при незначительных колебаниях температуры газа в газопроводе. Т.е. полагаем, что в газопроводе соблюдается условие: Т = constи η = const.При таких условиях:
= const.При этом объёмный расход Qv газа будет меняться от одного сечения газопрово-да к другому, т.к. плотность газа зависит от давления, которое по длине газопровода меняется. При этом должна изменяться и температура газа по длине газопровода, и, как следствие, также и вязкость газа. Однако для решения практических задач движе-ние газа по трубопроводу можно считать изотермическим (небольшие скорости движения, теплоизоляция газопровода, небольшие перепады давления). Это допущение не приведет к серьёзным погрешностям в расчётах, но оно позволяет пренебречь изменением вязкости газа при незначительных колебаниях температуры газа в газопроводе. Т.е. полагаем, что в газопроводе соблюдается условие: Т = constи η = const.При таких условиях:  =
= 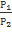 . Для всего потока постоянным будет число Рейнольдса, и, как следствие, будут одинаковым коэффициенты трения и гидравлических сопротивлений по длине потока.
. Для всего потока постоянным будет число Рейнольдса, и, как следствие, будут одинаковым коэффициенты трения и гидравлических сопротивлений по длине потока.
Объёмный расход: Qv = 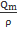 . в этом случае меня-ется от сечения к сечению. Тогда скорость движения газа также будет меняться вдоль длины газопровода. Так как массовый расход
. в этом случае меня-ется от сечения к сечению. Тогда скорость движения газа также будет меняться вдоль длины газопровода. Так как массовый расход  =
=  u
u  S = const (масса газа, движущегося по трубе, не меняется от сечения к сечению), то при постоянном диаметре трубы (S = const)скорость и плотность в сечениях связаны соотношением:
S = const (масса газа, движущегося по трубе, не меняется от сечения к сечению), то при постоянном диаметре трубы (S = const)скорость и плотность в сечениях связаны соотношением:
 =
= 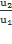 . u =
. u =  =
= 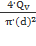 =
= 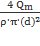 .
.
Число Рейнольдса: Re =  =
=  .
.
Отметим, что в последнем выражении все величины, входящие в правую часть равенства, являются величинами постоянными, отсюда: Re = const. По этой причине для определения величины потерь напора можно воспользоваться обычным уравнением Бернулли. Для горизонтальной трубы одинакового диаметра линейные потери определяются как:  = hλ. Средняя плотность определяется как сумма
= hλ. Средняя плотность определяется как сумма  =
=  .
.
Линейные потери можно определить, как и в случае с жидкостью по формуле Дарси:
hλ=  . В качестве скорости
. В качестве скорости  берут среднюю скорость u =
берут среднюю скорость u =  . Коэффициент линейных потерь (движение турбулентное, Re ≥ 4000) можно определить по формуле Альтшуля:
. Коэффициент линейных потерь (движение турбулентное, Re ≥ 4000) можно определить по формуле Альтшуля:  = 0,11 · (
= 0,11 · ( +
+  )0,25 или Блазиуса (для гидравлически гладких труб)
)0,25 или Блазиуса (для гидравлически гладких труб)  =
=  . Эквивалентную шероховатость берут из таблиц для жидкости.
. Эквивалентную шероховатость берут из таблиц для жидкости.
Задача 8. Массовый расход транспортируемого газа по трубе диаметром 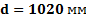 составляет
составляет 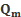 = 180
= 180  . Определить скорости движения газа в начальном и конечном сечениях, если плотность газа уменьшилась с
. Определить скорости движения газа в начальном и конечном сечениях, если плотность газа уменьшилась с  = 45
= 45 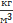 до
до 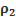 = 25
= 25 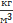 .
.
Решение.
Находим скорость движения газа в начальном сечении (на начальном участке газопровода):
u1 =  =
= 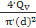 =
=  =
=  = 4,9
= 4,9  .
.
В конечном сечении (на конечном участке газопровода):
u2 =  =
= 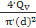 =
=  =
=  = 8,8
= 8,8  .
.
Вывод: уменьшение плотности газа вследствие его расширения за счёт падения давления (потери энергии на преодоление сил трения) приводит к увеличению скорости его движения при неизменном диаметре. В жидкостях в таких условиях скорость не меняется, так как жидкость практически несжимаема.
Задача 9. Определить потери давления на участке прямого газопровода длиной 100м и диаметром 1020 мм, ес-ли массовый расход газа (азота) составляет 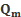 = 180
= 180  , а плотность газа уменьшилась с
, а плотность газа уменьшилась с  = 45
= 45 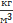 до
до 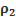 = 25
= 25 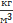 . Труба шероховатая, эквивалентная шероховатость составляет ∆э=0,1 мм (новая стальная труба). Коэффициент динамичес-кой вязкости (для азота) при нормальных условий принять равным η = 17,8
. Труба шероховатая, эквивалентная шероховатость составляет ∆э=0,1 мм (новая стальная труба). Коэффициент динамичес-кой вязкости (для азота) при нормальных условий принять равным η = 17,8  10-6 Па
10-6 Па  с.Для определения коэффициента линейных потерь λтр использовать формулу для жидкости.
с.Для определения коэффициента линейных потерь λтр использовать формулу для жидкости.
Решение.
Для определения потерь давления используем уравнение Бернулли для трубы одинакового диаметра и уравнение Дарси для линейных потерь напора:
 = hλ и hλ=
= hλ и hλ=  .
.
Определим средние значения плотности и скорости по длине газопровода:
ρср =  = 35
= 35  . u =
. u = 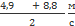 = 6,85
= 6,85  .
.
Число Рейнольдса:
Re =  =
=  = 12,6
= 12,6  106
106
Так как число Рейнольдса больше 560  (5,7
(5,7  106), то для нахождения коэффициента гидравлического трения исполь-зуем формулу Альтшуля в виде:
106), то для нахождения коэффициента гидравлического трения исполь-зуем формулу Альтшуля в виде:
 = 0,11 · (
= 0,11 · ( +
+  )0,25.
)0,25.
 = 0,11 · (
= 0,11 · ( )0,25 = 0,11
)0,25 = 0,11  (0,98
(0,98  10-4)0,25 = 0,011.
10-4)0,25 = 0,011.
Находим падение давления на данном участке газопровода:
Р1 – Р2 = ρср 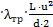 = 35
= 35 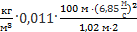 = 886 Па.
= 886 Па.
Тема 5. «Истечение жидкости из отверстия в тонкой стенке. Расчёт простого водопровода»
Задача 10. Из открытого резервуара, в котором поддерживается постоянный уровень, по стальному трубопроводу (эквивалентная шероховатость ∆ э) состоящему из труб различного диаметра d и различной длины L, вытекает в атмосферу вода, расход которой Q и температура t oС. Требуется: 1.Определить скорости движения воды и потери напора (по длине и местные) на каждом участке трубопровода. 2.Установить величину напора Н в резервуаре. 3.Построить напорную и пьезометрическую линии (можно без соблюдения масштаба).
Пусть d1= d3 = 15 мм, d2 = 20 м м, длины всех трёх участков одинаковы и равны L1= L2= L3= 1 м. Расход жидкости принимаем равным Q = 30  . Эквивалентную шерохова-тость труб принимаем равной ∆э= 0,1 мм
. Эквивалентную шерохова-тость труб принимаем равной ∆э= 0,1 мм
Решение.
.Запишем уравнение Бернулли для сечений 1-1 и 5-5: (только для этих сечений известны давления Р1=Рат и Р5=Рат): [ 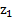 +
+  +
+ 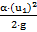 ]= [
]= [  +
+  +
+  ] + h1-5
] + h1-5

Рис.6 к задаче 10.
За нулевой уровень удобно принять плоскость, проходя-щую через ось трубопровода О-О. В этом случае z1=Н, z5=0. Средняя скорость в сечении 1-1 гораздо меньше скорости в сече-нии 5-5. Это следует из уравнения неразрывности струи:u1 · S1 = u5 · S5; u5 = u4 -5 u1 · (D2)= u5 · (d52) следует, что скорость жидкости на первом участке 1-2 гораздо меньше ско-рости на участке 4-5 и ею можно пренебречь. Скорость в пятом сечении-это скорость на участке 4-5, в 4-ом –на участке 3-4, в третьем -2-3. В принципе, эти обозначения условны. При расчётах линейных и местных потерь напора, как будет показано ниже, выбираются скорости на конкретных участках.С учётом сказанного, уравнение Бернулли для данного случая принимает следующий вид: Н = α5·[ 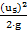 ]+ h1-5 Величина напора в резервуаре идёт на создание скоростного напора и на преодоление всех потерь напора, чтобы донести нужный расход (задаваемый расход) до конца трубопровода.Коэффициент Кориолиса α5= 1 для турбулентного течения и α5=2 для ламинарного течения. Чтобы определить вид движения жидкости, рассчитаем число Рейнольдса, для участка 4-5.Re =
]+ h1-5 Величина напора в резервуаре идёт на создание скоростного напора и на преодоление всех потерь напора, чтобы донести нужный расход (задаваемый расход) до конца трубопровода.Коэффициент Кориолиса α5= 1 для турбулентного течения и α5=2 для ламинарного течения. Чтобы определить вид движения жидкости, рассчитаем число Рейнольдса, для участка 4-5.Re = 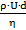 ; при температуре 200С плотность воды ρ = 103
; при температуре 200С плотность воды ρ = 103  , динамическая вязкостьη = 10-3 Па с.
, динамическая вязкостьη = 10-3 Па с.
Скорость на участке 4-5: u5=  =
= 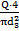 u5=
u5=  =2,83
=2,83 
 Re4-5 = Re2-3 =
Re4-5 = Re2-3 =  = 42460.
= 42460.
( = 1,5
= 1,5  10-2 м) Это турбулентный режим движения, α5=1.На участке 3-4 значение скорости u3=
10-2 м) Это турбулентный режим движения, α5=1.На участке 3-4 значение скорости u3=  =
= 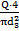 =
= 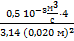 = 1,59
= 1,59  .
.
Re3-4=  = 31800. Это так же турбулентный режим течения жидкости.
= 31800. Это так же турбулентный режим течения жидкости.
Полные потери напора на участке 1-5 (h1-5) складываются из линейных потерь на участках между сечениями 1-2, 2-3, 3-4 и 4-5 и местных потерь в сечениях 2-2, 3-3 и 4-4.
h1-5 = h1-2 л+ h2-3 л+ h3-4 л+ h4-5 л+ h2 м+ h3 м+ h4 м.
Для нахождения линейных потерь используем формулу Дарси:h л= λтр · (  ) ·
) ·  .
.
На участке 1-2 (между сечениями 1-1 и 2-2) линейные потери малы и ими можно пренебречь. На участке 2-3, 3-4 и 4-5:
h2-3 л= λ2тр · (  ) ·
) · 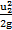 ; h3-4 л= λ3тр ·(
; h3-4 л= λ3тр ·(  ) ·
) ·  .
.
h4-5 л=λ4тр · 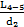 ) ·
) · 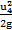 .
.
Местные потери в сечениях 2-2, 3-3 и 4-4 находим по формуле Вейсбаха
h2 м= ε2· 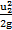 ; h3 м= ε3·
; h3 м= ε3· 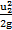 ; h4 м= ε4·
; h4 м= ε4· 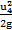 .
.
При внезапном расширении в сечениях (2-2) и (4-4) скорость выбирается после местного сопротивления (u2 и u4), а при внезапном сужении в сечении (3-3) скорость выбирается до местного сопротивления (u2).Из справочника находим:ε2 =0,5 (выход из бака в трубу). Для внезапного расширения при отноше-нии  = 0,56 ε3 =0,19. Для внезапного сужения при
= 0,56 ε3 =0,19. Для внезапного сужения при
 = 0,56 ε4 = 0,22.
= 0,56 ε4 = 0,22.
Значения скорости на участке 2-3 и 4-5 одинаковы и равны: u5 =u2-3 = u4-5= 2,83  . Для нахождения коэффициента гидравлического трения на участке 2-3 необходимо подобрать формулу из соответствующей области турбулентного режима. Для этого вначале рассчитаем значения: 10
. Для нахождения коэффициента гидравлического трения на участке 2-3 необходимо подобрать формулу из соответствующей области турбулентного режима. Для этого вначале рассчитаем значения: 10  =
=  = 1500 и 560
= 1500 и 560  =
=  = 84100. 4000<42460 <84000. Это вторая область турбулентного течения Для расчёта коэффициента гидравлического трения выбираем формулу Альтшуля:
= 84100. 4000<42460 <84000. Это вторая область турбулентного течения Для расчёта коэффициента гидравлического трения выбираем формулу Альтшуля:
λ2-3=0,11( +
+  )0,25= 0,11(0,0067+ 0,0016)0,25 = 0,033 λ 3-4=0,11(
)0,25= 0,11(0,0067+ 0,0016)0,25 = 0,033 λ 3-4=0,11( +
+  )0,25= 0,11(0,005 + 0,002)0,25 =0,032. λ4-5= λ2-3=0,033
)0,25= 0,11(0,005 + 0,002)0,25 =0,032. λ4-5= λ2-3=0,033
Расчёты показывают, что коэффициент линейных (гидравлических) потерь по всей длине трубы примерно одинаков: λ=0,03.
Находим линейные потери напора на всех трёх участках:
h2-3 л = h4-5л =λ2тр·  ) ·
) · 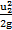 ;
;
h2-3 л = 0,03 ·( 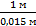 ) · [
) · [ 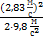 ] = 0,82 м.
] = 0,82 м.
h3-4 л= λ2тр ·  ) ·
) ·  .
.
h3-4 л = 0,03 · ( ) · [
) · [  ] = 0,19 м.
] = 0,19 м.
Находим местные потери:
h2 м= ε2· 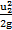 =0,5 · [
=0,5 · [ 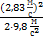 ] = 0,20 м
] = 0,20 м
h3 м= ε3· 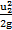 = 0,19 ·
= 0,19 · 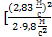 ] = 0,08 м.
] = 0,08 м.
h4 м= ε4· 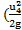 ) =0,22 ·
) =0,22 · 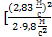 ] = 0,09 м.Полные потери напора на участке 1-5:
] = 0,09 м.Полные потери напора на участке 1-5:
h1-5 = h1-2 л+ h2-3 л+ h3-4 л+ h4-5 л+ h2 м+ h3 м+ h4 м.
h1-5 = 0+0,82 м +0,19 м+ 0,82 м+0,20 м+0,08 м+0,09 м=2,2 м. Величина напора в резервуаре:
Н = α5·[  ]+ h1-5 = [
]+ h1-5 = [ 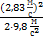 ]+2,2 м = 0,41 м +2,2 м = 2,61 м.
]+2,2 м = 0,41 м +2,2 м = 2,61 м.
Вернёмся ещё раз к уравнению Бернулли: [ 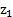 +
+  +
+ 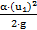 ]= [
]= [  +
+  +
+  ] + h1-2
] + h1-2
В левой части сумма 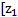 +
+  +
+  называется напором в первом сечении. Он всегда больше, чем напор во втором сечении
называется напором в первом сечении. Он всегда больше, чем напор во втором сечении  +
+  +
+  на величину потерь h1-2 . Следовательно, чтобы найти напор во втором сечении, надо из значений напора в сечении 1 вычесть потери напора.
на величину потерь h1-2 . Следовательно, чтобы найти напор во втором сечении, надо из значений напора в сечении 1 вычесть потери напора.
Напорную. линию строим следующим образом. Откладываем вдоль вертикальной оси(трубопровод начинается в сечении (2-2)) Н= 2,61 м. В сечении (2-2) теряется на местном сопротивлении (вход в трубу) h2 м= 0,20 м. При движении жидкости по трубе на участке между сечениями (2-2) и (3-3) в виде линейных потерь напора теряется h2-3 л =0,82 м. Местные потери напора в сечении (3-3) равны h3 м= 0,08 м.
Линейные потери на участке (3-4) составляют h3-4 л = 0,19 м. Местные потери в сечении (4-4) h4 м= 0,09 м. Линейные потери на участке (4-5) h4-5л = 0,82 м. Соединяем полученные точки и строим напорную линию. Для построения пьезометрической линии из значений напора в соответствующих точках вычитаем скоростной напор ( ). На участках (2-3) и (4-5)
). На участках (2-3) и (4-5) 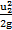 = 0,41 м, а на участке (3-4) скоростной напор
= 0,41 м, а на участке (3-4) скоростной напор  = 0,13 м.
= 0,13 м.
На участке (4-5) скоростной напор 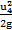 =0,41 м. Соеди-няем полученные токи прямыми и получаем пьезометрическую линию.
=0,41 м. Соеди-няем полученные токи прямыми и получаем пьезометрическую линию.

Рис. 7. Примерное изображение напорных линий (полного и пьезометрического напоров).
Примечание: рисунок выполнен не в масштабе.
Тема 6. «Гидронасосы. Гидродвигатели. Гидропривод»
Задача 11. При испытании насоса получены следующие данные: избыточное давление на выходе из насоса Р2=0,35 МПа, вакуум перед входом в насос hвак= 294 мм.рт.ст.; подача насоса Q=6,5  , крутящий момент на валу насоса М=41 Н
, крутящий момент на валу насоса М=41 Н  м; частота вращения вала насоса n = 800
м; частота вращения вала насоса n = 800  . Определить мощность, развиваемую насосом, потребляемую мощность и к.п.д. насоса. Диаметры всасывающего и напорного трубопроводов считать одинаковыми.
. Определить мощность, развиваемую насосом, потребляемую мощность и к.п.д. насоса. Диаметры всасывающего и напорного трубопроводов считать одинаковыми.
Решение.
Полезная мощность (мощность, сообщаемая насосом жидкости):
Nп = Р  Q= (Р2- Рвак)
Q= (Р2- Рвак)  Q= (Р2+hвак
Q= (Р2+hвак  ρрт
ρрт  g)
g)  Q. Nп = (3,5
Q. Nп = (3,5  105 Па +0,392
105 Па +0,392  105 Па)
105 Па)  6,5
6,5  10-3
10-3  = 25,3
= 25,3  102 вт =2,53 квт. Потребляемая мощность Nпотр= М
102 вт =2,53 квт. Потребляемая мощность Nпотр= М  ω = М
ω = М  2π n. Nпотр= 41Нм
2π n. Nпотр= 41Нм  2 •3,14
2 •3,14  (
( ) = 3,43 квт.
) = 3,43 квт.
К.п.д. =  =
=  = 0,74.
= 0,74.
Ответ: Nп = 2,53 квт; Nпотр= 3,43 квт; К.п.д. = 0,74.
Задача 12. Двухкамерный гидродвигатель поворотного движения должен создавать момент на валу, равный М=2 кН  м при угловой скорости поворота ω=2 с-1. Размеры гидро-двигателя: внутренний диаметр D=200 мм, d=100 мм, ширина лопастей b = 60 мм, объёмный кпд η0 = 0,75, механический кпд ηмех = 0,9. Определить потребное давление насоса и необ-ходимую подачу.
м при угловой скорости поворота ω=2 с-1. Размеры гидро-двигателя: внутренний диаметр D=200 мм, d=100 мм, ширина лопастей b = 60 мм, объёмный кпд η0 = 0,75, механический кпд ηмех = 0,9. Определить потребное давление насоса и необ-ходимую подачу.
Решение.
Угловую скорость вращения вала шиберного поворотного двигателя с учётом потерь определяют по формуле: ω =  ; Здесь z – число шиберов. Отсюда находим расход: Q =
; Здесь z – число шиберов. Отсюда находим расход: Q = 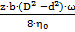 ;
;
Q =  = 1,2
= 1,2  10-3
10-3 
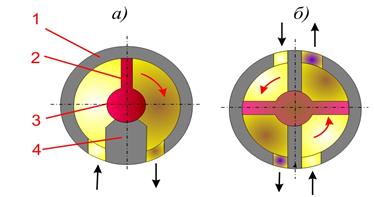
Рис. 8 к задаче 12. Шиберные (поворотные) гидродвигатели:
а) одношиберный; б) двухшиберный
1-корпус; 2-пластина (шибер);3-поворотный ротор; 4-перемычка.
Момент на валу поворотного двигателя: М= 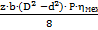 ; Отсюда находим потребное давление: Р =
; Отсюда находим потребное давление: Р = 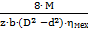 ; Р=
; Р= 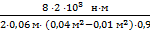 = 4,94
= 4,94  106 Па= 4,94 МПа.
106 Па= 4,94 МПа.
Ответ: потребное давление: Р = 4,94 МПа.
Задача 13. Определить давление, создаваемое насосом, и его подачу, если преодоле-ваемая сила вдоль штока F=10 кН, а скорость перемещения поршня υп= 0,1  . Учесть потерю давления на трение в трубопроводе, общая длина которого l =8 м; диаметр d=14 мм. Каждый канал распределителя по сопротивлению эквивалентен длине трубопровода l э=100 d. Диаметр поршня D=100 мм, площадью штока пренебречь. Вязкость масла ν = 1 Ст; плотность ρ =900
. Учесть потерю давления на трение в трубопроводе, общая длина которого l =8 м; диаметр d=14 мм. Каждый канал распределителя по сопротивлению эквивалентен длине трубопровода l э=100 d. Диаметр поршня D=100 мм, площадью штока пренебречь. Вязкость масла ν = 1 Ст; плотность ρ =900  .
. 
Рис. 9 к задаче 13.
Решение:
Примечание: единицей измерения кинематической вязкости (ν =  ) в системе СИ является величина (
) в системе СИ является величина ( ). Часто на практике используется величина 1 ст(стокс) = 10-4
). Часто на практике используется величина 1 ст(стокс) = 10-4  .
.
Давление на выходе насоса идёт на преодоление усилия на штоке ∆Р и давления потерь в трубопроводе Рпот: Рн = ∆Р + Рпот.
Для поршневого гидроцилиндра F 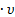 п = ∆Р
п = ∆Р  S, где S-площадь поршня. Находим ∆Р.
S, где S-площадь поршня. Находим ∆Р.
Площадь поршня S=  .
.
∆Р =  =
=  = 1,274•106Па = 1,274 МПа
= 1,274•106Па = 1,274 МПа
Для нахождения давления потерь: Рпот=ρ  g
g  hпот необходимо найти полные потери напора в трубопроводе. Они складываются из линейных потерь hпотл и потерь в гидрораспределителе hр. hпот= hпотл + hр.
hпот необходимо найти полные потери напора в трубопроводе. Они складываются из линейных потерь hпотл и потерь в гидрораспределителе hр. hпот= hпотл + hр.
Для их нахождения используем формулу Дарси:
hпотл = λ  ; hр = λ
; hр = λ  ;
;
Скорость движения жидкости в трубопроводе определим из формулы расхода:
Q = U  Sж Здесь U – скорость движения жидкости по трубе,Sж=
Sж Здесь U – скорость движения жидкости по трубе,Sж= 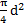 -площадь живого сечения потока.
-площадь живого сечения потока.
Расход жидкости, поступающей в гидроцилиндр, определяем из соотношения:
Q = υп  Sп = 0,1
Sп = 0,1  = 0,785
= 0,785  10-3 (
10-3 ( ).
).
U =  =
= 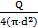 =
=  = 5,10
= 5,10 
Для нахождения коэффициента гидравлического трения λ тр рассчитаем число Рейнольдса:
Re =  =
=  =
=  = 714. Для нахождения λтр используем формулу Пуайзеля:
= 714. Для нахождения λтр используем формулу Пуайзеля:
λтр =  =
= 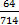 = 0,09.
= 0,09.
Находим давление, развиваемое насосом на выходе:
Рн =∆Р + Рпот = ∆Р + (hпотл + hр)  ρ
ρ  g
g
Рн = ∆Р + [(λ  ) + (λ
) + (λ  )])
)])  ρg
ρg
Рн=∆Р+ [ (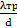 )
)  ]
]  (l+ l э)
(l+ l э) 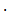 ρ
ρ 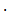 g];
g];
Рн=1,274 МПа+[  ]
] 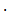 (8м + 2,8м)
(8м + 2,8м) 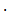 900
900  .Рн= 1,274 МПа + 0,813 МПа = 2,1 МПа.
.Рн= 1,274 МПа + 0,813 МПа = 2,1 МПа.
Размерность: 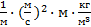 =
=






