Исследование НДС обводненного трубопровода с учетом параметров эксплуатации
Постановка задачи
Разработанный в п. 2.3 метод совместного интегрирования дифференциальных уравнений продольно-поперечного изгиба стержня, моделирующего НДС трубопровода, деформирующегося совместно с различными типами грунтов, является универсальным. Применим его для исследования влияния параметров эксплуатации (
внутреннее давление, 
температурный перепад) на НДС обводненного трубопровода.
Для упрощения анализа принимаем, что трубопровод составлен из прямолинейных труб. Обводненный участок находится в середине рассчитываемого участка, примыкающие к нему слева и справа подземные участки идентичны. По длине рассчитываемого участка не изменяются физико-механические характеристики грунтов, глубина заложения трубы. Концы рассчитываемого участка защемлены грунтом. Таким образом, обеспечивается горизонтальное положение трубы. Только при выполнении вышеперечисленных условий дифференциальные уравнения продольно-поперечного стержня в упругой среде, моделирующего трубопровод, допускается решение в конечных аналитических выражениях, представленных в п. 2.2.
Таким образом, средняя часть длиной ℓ соответствует обводненной части, т.е. находится под водой. Примыкающие к ней слева и справа части являются подземными.
На обводненной части трубопровода в зависимости от уровня воды относительно поперечного сечения трубы действует вертикально направленная вверх выталкивающая сила воды. Величина ее, приходящаяся на единицу длины газопровода, определяется по формуле [8]
где 
удельный вес воды.
Высота засыпки грунта подземных участков соответствует проектной. Здесь трубопровод деформируется под действием собственного веса, веса перекачиваемой среды и давления грунта на трубу, при определении которого учитывается наличие или отсутствие свода естественного равновесия грунта на трубе. Грунт основания при совместной деформации с трубой моделируется основанием Винклера. Как и в п. 2.2, рассмотрим три варианта постановки задачи НДС подземных участков, которое описывается дифференциальными уравнениями (2.64, 2.74, 2.81), а их решение имеет вид (2.67, 2.76, 2.82), а для обводненной части эти уравнения представлены в (2.16, 2.34, 2.45), а их решение (2.19, 2.36, 2.49).
По сравнению с решениями (2.19, 2.36, 2.49) в средней обводненной части вертикальная составляющая нагрузки зависит от выталкивающей силы воды, определяемой по формуле (2.89).
Анализ результатов расчетов
Далее представим результаты расчета НДС трубопровода, средняя часть которого длиной ℓ= 59,3 м находится под водой. Остальные условия идентичны случаю надземного перехода с примыкающими подземными участками. Для выявления воздействия выталкивающей силы воды вначале рассмотрим случай, когда в трубе отсутствует перекачиваемый продукт. Вес трубы длиной 1 м составляет 3,60 кН/м, выталкивающая сила воды на 1 м трубы равна 9,6 кН/м. Вертикальная составляющая нагрузки в обводненной части равна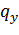 
= 9,6 – 3,6 = 6,0 кН/м и направлена вверх, что означает положительную плавучесть трубы. На рисунке 2.14 представлены эпюры основных характеристик НДС трубопровода: поперечная сила, изгибные напряжения, угол поворота продольной оси трубы и стрела подъема. Обозначения эпюр для каждого из 3-х вариантов постановки задач совпадают с соответствующими ранее принятыми обозначениями.
Анализ эпюр рисунка 2.14 показывает совпадение результатов решения по второму и третьему варианту постановки задачи. Это объясняется тем, что при отсутствии внутреннего давления закрытая задвижка (заглушка), которая моделирует работу компенсатора, не может растягивать трубопровод в продольном направлении. В первом варианте постановки задачи защемленный на концах рассчитываемый участок испытывает дополнительный изгиб в обводненной части за счет воздействия температурных напряжений. Для оценки влияния этого воздействия
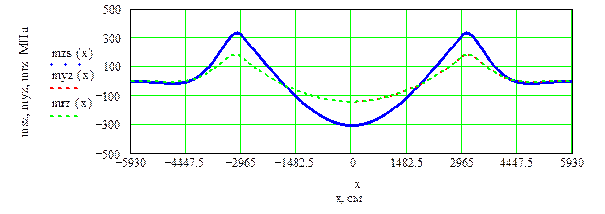
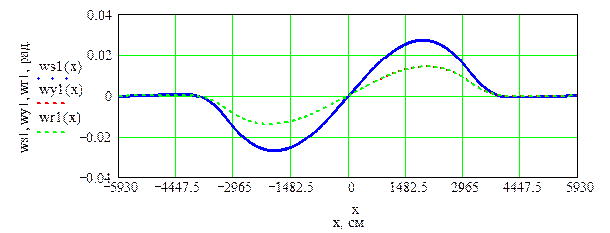
Рисунок 2.14 – Расчет основных характеристик НДС подводного перехода газопровода (l0=59.3 м, Egr=10 МПа, p0= 0, dt=40 0C, Sx=4536 кН, Sp= 0 кН, Nx= -4536кН)
представим в таблице 2.11 максимальные значения стрелы подъема в середине пролета и изгибные напряжения от пролетных и опорных изгибающих моментов для грунта с характеристиками 
= 10 МПа, 
=0,4 и параметрами эксплуатации 
=0 МПа, 
= 40оС.
Таблица 2.11 – Максимальные значения стрелы подъема и изгибных напряжений от пролетных и опорных изгибающих моментов (
= 0 МПа, 
= 40оС)
| Вариант постановки задачи | Стрела подъема, см | Изгибные напряжения, МПа | |
| от пролетных изгибающих моментов | от опорных изгибающих моментов | ||
| Первый |  = - 60,85
|  = -305,9
|  = 329,1
|
| Второй |  = - 31,2
|  = -145,2
|  = 178,9
|
| третий |  = - 31,2
|  = -145,2
|  = 178,9
|
Анализ данных таблицы 2.11 показывает, что воздействие температурных напряжений увеличивает стрелу подъема и изгибные напряжения от пролетных и опорных изгибающих моментов в 2 раза.
Практический интерес представляют результаты расчета НДС трубопровода, находящегося под воздействием внутреннего рабочего давления и температурных напряжений.
Вес 1 м трубы с газом под давлением 7,5 МПа составляет
= 3,6 + 0,7 = 4,3 кН/м.
Выталкивающая сила воды на 1 м трубы равна 9,6 кН/м. Вертикальная составляющая нагрузки на 1 м трубы в обводненной части равна 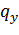= 9,6 – 4,3 = 5,3 кН/м и направлена вверх, что означает положительную плавучесть трубы.
Уменьшение величины положительной плавучести трубы под давлением по сравнению с трубой без давления на 0,7 кН/м должно привести к уменьшению стрелы подъема и характеристик НДС в обводненной части. Представленные на рисунке 2.15 эпюры основных характеристик НДС трубопровода, а также максимальные значения этих характеристик в таблице 2.12, показывают обратную картину.
Рисунок 2.15 – Расчет основных характеристик НДС подводного перехода газопровода (l0=59.3 м, Egr=10 МПа, p0= 75 МПа, dt=40 0C, Sx=7110 кН, Sp=6369 кН, Nx=-675,3 кН)
Таблица 2.12 – Максимальные значения стрелы подъема и изгибных напряжений от пролетных и опорных изгибающих моментов ( = 7,5 МПа, = 40оС)
| Вариант постановки задачи | Стрела подъема, см | Изгибные напряжения, МПа | |
| от пролетных изгибающих моментов | от опорных изгибающих моментов | ||
| Первый | = 114,2
| = -609,5
| = 596,9
|
| Второй | = 27,2
| = -127,4
| = 157,0
|
| третий | = 14,0
| = -69,2
| = 89,8
|
Анализ данных таблицы 2.12 говорит о том, что воздействие внутреннего рабочего давления и температурных напряжений приводит к увеличению стрелу подъема в 4 раза, к увеличению изгибных напряжений от пролетных изгибающих моментов в 5 раз, к увеличению изгибных напряжений от опорных изгибающих моментов в 4 раза.
Не уменьшение, а существенное возрастание стрелы подъема газопровода под давлением, на который действует меньшая выталкивающая сила по сравнению с газопроводом без давления, объясняется воздействием на изгиб внутреннего рабочего давления и температурных напряжений.
Растяжение трубопровода под воздействием внутреннего рабочего давления на закрытую задвижку (заглушку), которая моделирует работу компенсатора, приводит к уменьшению максимального значения стрелы подъема в середине пролета в 8 раз, изгибных напряжений от пролетных – в 9 раз, опорных изгибающих моментов – в 6,5 раза.
Исследуем влияние состояния грунта прилегающих подземных участков на НДС обводненного трубопровода. Выполним расчет НДС после выполнения мероприятий по повышению жесткости грунта прилегающих участков. Результаты расчета приведены на эпюрах рисунка 2.16 и в таблице 2.13.
Таблица 2.13 – Максимальные значения стрелы подъема и изгибных напряжений от пролетных и опорных изгибающих моментов ( = 7,5 МПа, = 40оС) для 
=40МПа, 
=0,2
| Вариант постановки задачи | Стрела подъема, см | Изгибные напряжения, МПа | |
| от пролетных изгибающих моментов | от опорных изгибающих моментов | ||
| Первый | = 74,8
| = -424,4
| = 461,9
|
| Второй | = 23,2
| = -116,2
| = 162,5
|
| третий | = 14,3
| = -65,9
| = 108,3
|
Анализ данных таблицы 2.13 показывает, что воздействие внутреннего рабочего давления и температурных напряжений приводит к увеличению стрелы подъема в 3 раза, к увеличению изгибных напряжений от пролетных изгибающих моментов в 3,5 раза, к увеличению изгибных напряжений от опорных изгибающих моментов в 3 раза.
Растяжение трубопровода под воздействием внутреннего рабочего давления на закрытую задвижку (заглушку), которая моделирует работу компенсатора, приводит к уменьшению максимального значения стрелы подъема в середине пролета в 5 раз, изгибных напряжений от пролетных – в 6,5 раз, опорных изгибающих моментов – в 4 раза.
Таким образом, укрепление жесткости грунта привело к уменьшению стрелы подъема обводненной части в 1,5 раза, изгибных напряжений от пролетных изгибающих моментов – в 1,5 раза, от опорных – в 1.3 раза (для первого варианта постановки задачи).
Подобное сравнение для третьего варианта постановки задачи показывает, что вышеуказанные характеристики НДС практически не меняются. Это говорит о том, что при ослаблении состояния грунта трубопровод с компенсатором находится в стабильном положении, т.к. его характеристики НДС остались практически без изменения. Следовательно, установка компенсирующих устройств на обводненном трубопроводе оказалось более эффективным мероприятием по сравнению с укреплением жесткости грунта.
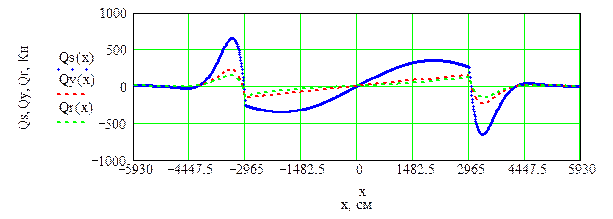
Рисунок 2.16 – Расчет основных характеристик НДС подводного перехода газопровода (l0=59.3 м, Egr=40 МПа, p0= 75 МПа, dt=40 0C, Sx=7110 кН, Sp=6369 кН,
Nx=-675,3 кН)
В ранних исследованиях проводится оценка уменьшения продольного усилия от применения различных конструкций компенсаторов. При этом отсутствует учет влияния уменьшения изгибных напряжений при растяжении трубопровода компенсатором.
В работе [8] при численном моделировании НДС подземных трубопроводов с произвольным очертанием оси воздействие внутреннего давления на изгиб трубопровода с компенсатором учитывалось заданием эквивалентного продольного усилия в уравнениях продольно-поперечного изгиба трубопровода, а также заданием продольной растягивающей силы в граничных условиях на концах рассчитываемого участка. Такое описание НДС трубопровода с компенсатором является некорректным, т.к. в этом случае сила растяжения уничтожается эквивалентным продольным усилием. В результате эта постановка задачи не учитывает воздействие давления на компенсатор, растягивающий трубопровод.
В предложенной нами постановке задачи НДС трубопровода с компенсатором моделируется классическим уравнением продольно- поперечного изгиба полого стержня при его растяжении [181]. Здесь, в отличие от задачи о НДС защемленного на концах трубопровода грунтом, физическая картина деформации при изгибе трубопровода и стержня совпадает. Защемленный на концах трубопровод испытывает дополнительный изгиб от воздействия эквивалентного продольного усилия, возникающего как равнодействующая сила от воздействия внутреннего давления за счет разности площадей по нижней и верхней части поверхности трубы. Стержень в классической теории стержней испытывает дополнительный изгиб от воздействия внешней сжимающей силы, приложенной на его концах. При этом сами уравнения для трубопровода и стержня совпадают, а продольная сила и эквивалентное продольное усилие имеют разный физический смысл.
