Пусть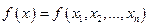 
- дифференцируемая функция, заданная на 
, а 
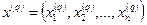- некоторая текущая точка. Правил, касающихся выбора начальной точки (начального приближения) 
, не существует, однако по возможности она должна находиться вблизи от искомого оптимального плана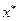 
. Если 
- нестационарная точка (т. е. 
), то при движении в направлении 
функция 
на некотором промежутке обязательно будет возрастать. Отсюда возникает естественная идея такого выбора шага, чтобы движение в указанном направлении продолжалось до тех пор, пока возрастание не прекратится. Для этого выразим зависимость значения от шагового множителя 
, полагая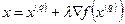 
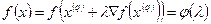(9)
или, в координатной форме,
. (10)
Чтобы добиться наибольшего из возможных значений f при движении по направлению , нужно выбрать такое значение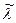 
, которое максимизирует функцию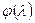 
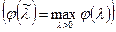. Для вычисления 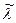, используется необходимое условие экстремума 
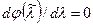. Заметим, что если для любого 
, то функция не ограничена сверху (т. е. не имеет максимума). В противном случае, в силу (10) получаем
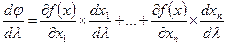, (11)
что, в свою очередь, дает
. (12)
Если считать, что следующая точка 
соответствует оптимальному значению 
, то в ней должно выполняться условие 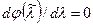, и 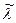следует находить из условия 
или
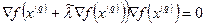. (13)
Условие (13) означает равенство нулю скалярного произведения градиентов функции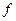 
точках 
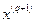и .Геометрически это условие может быть интерпретировано как перпендикулярность векторов градиентов функции f в указанных точках, что и показано на Рис. 2.2. Продолжая геометрическую интерпретацию метода наискорейшего спуска, отметим, что в точке 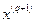вектор 
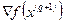, являясь градиентом, перпендикулярен линии уровня, проходящей через данную точку. Следовательно, вектор 
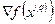является касательным к этой линии. Таким образом, движение в направлении градиента 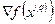следует продолжать до тех пор, пока он пересекает линии уровня оптимизируемой функции.
После того как точка 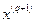найдена, она становится текущей для очередной итерации. На практике признаком достижения стационарной точки служит достаточно малое изменение координат точек, рассматриваемых на последовательных итерациях. Одновременно с этим координаты вектора 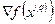должны быть близки к нулю.
Метод дробления шага
Для нахождения шага l, в методе наискорейшего спуска требуется решить уравнение (13), которое может оказаться достаточно сложным. Поэтому часто ограничиваются «подбором» такого значения l, что 
. Для этого задаются некоторым начальным значением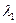 
(например, 
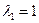и проверяют условие 
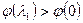. Если оно не выполняется, то полагают
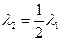
и т. д. до тех пор, пока не удается найти подходящий шаг, с которым переходят к следующей точке 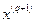. Критерий завершения алгоритма, очевидно, такой же, как и в методе наискорейшего спуска.
