Отношения между множествами

Два множества A и B могут вступать друг с другом в различные отношения.

· Множество Aвключено в B, если каждый элемент множества A принадлежит также и множеству B (рис. 1.2 а), 1.2 б). Частным случаем отношения включения может быть и равенство множеств A и B, что отражается символом Í: A Í B Û " a Î A ® a Î B.

Подобное отношение можно называть нестрогим включением. Довольно часто требуется исключить равенство множеств из отношения включения, в связи с чем, вводится отношение строгого включения.

· Множество Aстрого включено в B, если A включено в B, но не равно ему (рис. 2а), что отражается символом Ì: A Ì B Û (A Í B) и (A¹B).

В этом случае множество А называют собственным (строгим, истинным) подмножеством множества В. Примерами использования строгого включения могут являться: A Ì U, B Ì U, ÆÌ B, ÆÌ B.

Отношения между множествами могут обладать следующими свойствами: рефлексивностью, симметричностью и транзитивностью.

Свойство рефлексивности является унарным (одноместным), т.е. применительно к единственному объекту (в данном случае к множеству) и означает, что отношение применимо к «себе самому».

Простым примером рефлексивного отношения для чисел могут служить отношения «³» или «£», т.к. для любого числа d можно записать d ³ d или d £ d. В свою очередь отношения «>» и «<» этим свойством не обладают, в связи с чем они называются антирефлексивными.

Свойство симметричности является бинарным (двухместным), т.е. применимо к двум объектам. Отношение является симметричным, если оно выполняется в обе стороны по отношению к паре объектов (в данном случае множеств). Примерами свойства симметричности являются различные геометрические объекты, для которых понятие «симметрии» является наиболее наглядным. Например, отношение: «быть симметричными относительно оси х» в отношении точек плоскости является симметричным. Действительно, если первая точка симметрична второй, то вторая точка обязательно симметрична первой.

В свою очередь, отношение между двумя объектами не обладает свойством симметричности, т.е. является антисимметричным, если его выполнение в обе стороны имеет место только в случае равенства объектов.

Если записать бинарное отношение между объектами a и b в общем виде aRb, где R – символ отношения, то для симметричного отношения: aRb® bRa при любых a и b, а для антисимметричного aRb® bRa, только, если a = b.

Примером антисимметричного отношения могут служить отношения «³» или «£» между числами. Действительно, (a £ b) ® (b £ a), только, если a = b.

Свойство транзитивности является тернарным (трехместным), т.е. применяется к трем объектам. Отношение R между объектами a, b, с является транзитивным, если из aRb и bRс следует aRс, т.е. из выполнения отношения R между парами объектов (a, b) и (b, с) следует его выполнение и для пары (a, с). Примерами транзитивного отношения для чисел являются отношения «>», «³», «<», «£».

Отношение, не обладающее свойством транзитивности, называется нетранзитивным. Примером нетранзитивного отношения между множествами может служить отношение «пересекаться». Действительно для множеств: A= { a, b }, B= { b, c }, C= { c, d } A пересекается с B, B пересекается с C, но A не пересекается с C.

Отношение нестрогого включения обладает свойствами:

- рефлексивности: А Í А;

- антисимметричности: (A Í В и B Í A) ® (A=B);

- транзитивности: (A Í В и B Ì C) ® (A Ì C).

Отношение строгого включения обладает свойствами:

- антирефлексивности: А Ë А;

- транзитивности: (A Ì В и B Ì C) ® (A Ì C).

Свойства симметричности или несимметричности для отношения строгого включения не рассматриваются, так как их рассмотрение предполагает случай равенства между объектами отношения.

Для комбинации отношений строгого и нестрогого включений:

- (A Í ВиB Ì C) ® (A Ì C);

- (A Ì ВиB Í C) ® (A Ì C).

· множество Aравно множеству B, если A и B включены друг в друга или, иначе, между ними существует отношение взаимного включения (рис. 1.2 б.):

A=B Û (A Í B) и (B Í A).

Вторая часть равенства указывает на наиболее типичный метод доказательства равенства множеств A и B, который заключается в доказательстве сначала утверждения АÍВ, а затем ВÍА.

Равные множества содержат одинаковые элементы, причем порядок элементов в множествах не существенен: A ={1, 2, 3} и В ={3, 2, 1} ® A=B.

· множества A и Bне пересекаются, если у них нет общих элементов (рис. 1.2 в):

A и B не пересекаются Û " a Î A ® a Ï B.

· множества A и Bнаходятся в общем положении, если существуют элемент, принадлежащий исключительно множеству A, элемент, принадлежащий исключительно множеству B, а также элемент, принадлежащий обоим множествам (рис. 1.2 г):

A и B находятся в общем положении Û $ a, b, c: [ (a Î A) и (a Ï B)] и [(b Î B) и (b Ï A)] и [(c Î A) и (c Î B)].

Рассмотрим отношения между числовыми множествами, для которых будем использовать следующие обозначения:

S – множество простых чисел;

N – множество натуральных чисел (т. е. N = {1, 2, 3, … });

Z – множество целых чисел;

Z + – множество целых неотрицательных чисел (иногда обозначается N ₀ (т. е. N ₀ = {0, 1, 2, 3, … }));

Z – – множество целых неположительных чисел;

R – множество действительных чисел;

R + – множество неотрицательных действительных чисел;

R – – множество неположительных действительных чисел;

V – множество рациональных чисел;

W – множество иррациональных чисел;

К – множество комплексных чисел.

Для этих множеств очевидными являются следующие цепочки отношений включения:

· S Ì N Ì Z + Ì Z Ì V Ì R Ì К;

· W Ì R Ì К.

Алгебра множеств

Множество всех подмножеств универсального множества U вместе с операциями над множествами образуют так называемую алгебру подмножеств множества U или алгебру множеств.

Основными составляющими алгебры множеств являются операции над множествами и свойства этих операций, которые формулируются в виде основных тождеств или законов алгебры множеств.

Операции над множествами

Над множествами определены следующие операции: объединение, пересечение, разность (относительное дополнение), симметрическая разность и дополнение (абсолютное).

Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1.3 а):

A È B = { x | x Î A или x Î B }.

Операцию объединения можно распространить на произвольное, в том числе и бесконечное количество множеств, например М = А È В È С È D. В общем случае используется обозначение 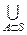А, которое читается так: “объединение всех множеств А, принадлежащих совокупности S ”.

Если же все множества совокупности индексированы (пронумерованы с помощью индексов), то используются другие варианты обозначений:

1. 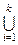А _i, если S ={ A₁,A₂,…,A_k };

2. А _i, если S – бесконечная совокупность пронумерованных множеств;

3. А _i, если набор индексов множеств задан множеством I.

Пример 1.2.

А= { a,b,c }, B= { b,c,d }, C= { c,d,e }.

A È B= { a,b,c,d }; A È C= { a,b,c,d,e }; B È C= { b,c,d,e }; A È B È C= { a,b,c,d,e }.

Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 1.3 б):

A Ç B = { x | x Î A иx Î B }.

Аналогично определяется пересечение произвольной (в том числе бесконечной) совокупности множеств. Обозначение для пересечения системы множеств аналогичны рассмотренным ранее обозначениям для объединения.

Пример 1. 3. (для множеств из примера 1.2):

А Ç В= { b,c }; A Ç C= { c }; B Ç C= { c,d }; A Ç B Ç C= { c }.

Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 1.3 в):

A \ B = { x | x Î A иx Ï B }.

Разность множеств А и В иначе называется дополнением множества А до множества В (относительным дополнением).

Пример 1. 4. (для множеств из примера 1.2)

А\В= { а, b, c } \ { b,c,d } = { a }.

Симметрической разностью множеств А и В называется множество, состоящее из элементов, которые принадлежат либо только множеству А, либо только множеству В (рис. 1.3 г). Симметрическую разность обозначают как A Δ B,A – B или A Å B:

A Δ B = { x | (x Î A иx Ï B) или (x Î В иx Ï А) }.

Таким образом, симметрическая разность множеств A и B представляет собой объединение разностей (относительных дополнений) этих множеств: A Δ B =(A\B) È (B\A).

Пример 1. 5. (для множеств из примера 1.2)

A Δ B = { a } È { d } = { a,d }.

Дополнением (абсолютным) множества А называется множество всех тех элементов х универсального множества U, которые не принадлежат множеству А (рис. 1.3 д). Дополнение множества А обозначается :

={ x ç x Ï A }= U \ A.

С учетом введенной операции дополнения разность множеств А и В можно представить в виде: A \ B = A Ç .

Операции над множествами используются для получения новых множеств из уже существующих. Порядок выполнения операций над множествами определяется их приоритетами в следующем порядке: , Ç, È, \, Δ.

 

Лекция 2. Основные тождества (законы) алгебры множеств

 

Основные тождества (законы) алгебры множеств

1. Коммутативные (переместительные) законы:

A È B= B È A; A Ç B= B Ç A.

2. Ассоциативные (сочетательные) законы:

A È (B È C)=(A È B) È C; A Ç (B Ç C)=(A Ç B) Ç C.

3. Дистрибутивные (распределительные) законы:

A È(B Ç C) = (A È B) Ç(A È C); A Ç (B È C) = (A Ç B) È (A Ç C).

Замечание. Эти законы выражают дистрибутивность объединения относительно пересечения (для первого) или дистрибутивность пересечения относительно объединения (для второго) слева. Операции объединения и пересечения обладают также свойством дистрибутивности справа:

(A È B) Ç C = (A Ç С) È (В Ç C); (A Ç B) È C = (A È С) Ç (В È C);

4. Законы тавтологии (идемпотентности ):

A È A= A; A Ç A= A.

5. Законы двойственности (де Моргана):

Огастес де Морган, (1806-1871) шотландский математик и логик

 

Следствия из законов двойственности: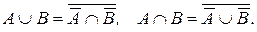

6. Законы поглощения: АÈ (АÇВ)=А; АÇ(АÈВ)=А.

7. Закон инволютивности: .

8. Закон противоречия: А Ç =Æ.

9. Закон «третьего не дано» (исключенного третьего): А È = U.

10. Свойства универсального множества: А È U = U; А Ç U = А.

11. Свойства пустого множества: А ÈÆ= А; А ÇÆ=Æ.

Дополнительные тождества для операций объединения, пересечения и дополнения множеств:

12. Законы склеивания:

13. Законы сокращения (законы Порецкого):

 

Порецкий Платон Сергеевич (1846 -1907) русский математик, астроном и логик

 

Следствия из законов сокращения: