1. Самостійно дати короткий опис роботи САК за принциповою схемою.
2. При вивченні конкретної САК її зручно попередньо формально розділити на типові елементи, виявити фізичні взаємозв'язки між цими елементами і відобразити їх в умовній формі на папері. Звичайно дослідження САК починають зі складання її функціональної схеми.
Для нашої системи функціональну схему можна представити у вигляді, наведеному на рис.1.8.
3. Складання диференціальних рівнянь окремих елементів САУ почнемо з рівняння генератора по каналу: 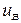 - вхід;
- вхід;  - вихід.
- вихід.
Скориставшись даними літературних джерел, можемо записати наступну систему рівнянь:
- рівняння електричної рівноваги ланцюга збудження (закон Кірхгофа)
 ;
;
- рівняння електричної рівноваги генератора
 ;
;
- нелінійне рівняння характеристики холостого ходу генератора
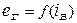 .
.
Спочатку приймемо допущення про те, що  і
і  , тобто
, тобто  (зневажимо втратами напруги в якірній обмотці генератора).
(зневажимо втратами напруги в якірній обмотці генератора).
Введемо нові змінні: 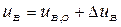 і
і  , де
, де 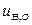 та
та  - значення відповідних змінних у точці стану рівноваги. Тоді
- значення відповідних змінних у точці стану рівноваги. Тоді
 . (7.1)
. (7.1)
Віднявши з рівняння (7.1) рівняння рівноваги 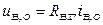 , одержимо наступне рівняння у відхиленнях:
, одержимо наступне рівняння у відхиленнях:
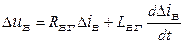 . (7.2)
. (7.2)
Далі зробимо лінеаризацію рівняння характеристики холостого ходу генератора на околицях точки рівноваги  :
:
 , (7.3)
, (7.3)
де  ;
;  - кут нахилу дотичної до характеристики холостого ходу в точці рівноваги.
- кут нахилу дотичної до характеристики холостого ходу в точці рівноваги.
Підставивши  з (7.3) в 7.(2), одержимо:
з (7.3) в 7.(2), одержимо:
 ,
,
або в стандартній формі і урахувавши, що ми прийняли  :
:
 , (7.4)
, (7.4)
де:  - постійна часу;
- постійна часу;  - передатний коефіцієнт генератора.
- передатний коефіцієнт генератора.
Відповідно до функціональної схеми складемо рівняння двигуна по каналу:  - вхід;
- вхід;  - вихід.
- вихід.
Для цього елемента, скориставшись даними літературних джерел, можемо записати наступну систему рівнянь:
- рівняння електричної рівноваги двигуна
 (7.5)
(7.5)
- рівняння руху привода
 . (7.6)
. (7.6)
Тут:  - обертальний момент, що розвиває двигун на валу;
- обертальний момент, що розвиває двигун на валу;  - конструктивний коефіцієнт;
- конструктивний коефіцієнт;  ;
;  - магнітний потік;
- магнітний потік;  - момент опору навантаження, приведений до валу двигуна.
- момент опору навантаження, приведений до валу двигуна.
Рівняння (7.6) перепишемо у вигляді:
 , де
, де  .
.
Звідки
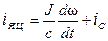 и.
и. 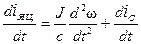
Підставимо два останніх співвідношення в рівняння (7.5) з урахуванням того, що  :
:
 .
.
Перетворимо отримане рівняння до стандартного вигляду
 .
.
Введемо позначення:
 - електромеханічна постійна часу:
- електромеханічна постійна часу:
 - електромагнітна постійна часу;
- електромагнітна постійна часу;
 - передатний коефіцієнт двигуна по напрузі;
- передатний коефіцієнт двигуна по напрузі;
 - передатний коефіцієнт двигуна по струму.
- передатний коефіцієнт двигуна по струму.
Тоді остаточно можемо записати:
 ,
,
або у відхиленнях
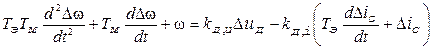 . (7.7)
. (7.7)
Таким чином, електродвигун можна представити математичною моделлю, що має два входи:  і
і  .
.
Рівняння напівпровідникового підсилювача по каналіу  - вхід,
- вхід, 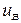 - вихід можна записати у вигляді:
- вихід можна записати у вигляді:
 ,
,
де  - передатний коефіцієнт.
- передатний коефіцієнт.
У відхиленнях це рівняння має схожий вигляд:
 .
.
Рівняння тахогенератора по каналу  - вхід,
- вхід,  - вихід, зневажаючи динамікою процесів у ньому, запишемо у вигляді:
- вихід, зневажаючи динамікою процесів у ньому, запишемо у вигляді:
 ,
,
де  - передатний коефіцієнт.
- передатний коефіцієнт.
Або у відхиленнях:
 .
.
Рівняння замикання контуру у відхиленнях у нашому випадку записується як:
 .
.
Надалі домовимося знак у рівняннях елементів не ставити, вважаючи всі змінні і їхні похідні малими відхиленнями від заданих значень. Тоді систему рівнянь САК можна представити в наступному вигляді
 (7.8)
(7.8)
Для визначення передатних функцій елементів системи використаємо інтегральне перетворення Лапласа рівнянь елементів (7.8) при нульових початкових умовах:
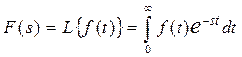 .
.
Одержимо наступну систему алгебраїчних рівнянь:
 (7.9)
(7.9)
Передатною функцією елемента САК по визначенню називається відношення її вихідної величини до вхідної, перетворених по Лапласу при нульових початкових умовах. Тоді, скориставшись співвідношеннями (7.9), після перетворень одержимо:
 .
.
4. У нашому випадку, скориставшись знайденими передатними функціями ланок, структурну схему можна представити у вигляді, приведеному на рис. 7.1.

Рис. 7.1
Скориставшись останньою схемою, знайдемо передатну функцію системи по каналу завдання:

 . (7.10)
. (7.10)
Відкіля можемо знайти характеристичне рівняння системи:
 .(7.11)
.(7.11)
Значення передатного коефіцієнта напівпровідникового підсилювача  визначимо, скориставшись алгебраїчним критерієм стійкості Гурвіца.
визначимо, скориставшись алгебраїчним критерієм стійкості Гурвіца.
Для цього складемо головний визначник нашої системи
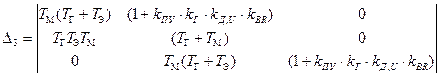 . (7.12)
. (7.12)
Звідси можна одержати визначник Гурвица 2-го порядку і зажадати, щоб він був більшим нуля:
 .(7.13)
.(7.13)
З нерівності (7.12) остаточно маємо:
 . (7.13)
. (7.13)
За остаточне значення  приймемо число, яке відповідає умові (7.13), а також забезпечує роботу двигуна зі швидкістю
приймемо число, яке відповідає умові (7.13), а також забезпечує роботу двигуна зі швидкістю  при рівні сигналу завдання
при рівні сигналу завдання  :
:
 . (7.14)
. (7.14)
5. Для визначення перехідної характеристики системи вирішимо алгебраїчне рівняння (7.9) відносно  при заданому
при заданому  :
:
 . (7.15)
. (7.15)
Визначимо оригінал рішення  .
.
У загальному випадку для знаходження  використовують зворотне перетворення Лапласа (
використовують зворотне перетворення Лапласа ( - перетворення), обумовлене формулою звертання Римана-Мелліна:
- перетворення), обумовлене формулою звертання Римана-Мелліна:
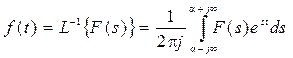 , (7.16)
, (7.16)
де 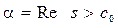 може бути будь-яким постійним числом
може бути будь-яким постійним числом 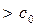 .
.
Найбільш простим методом є використання довідкових таблиць, у яких приводяться зображення  і відповідні їм оригінали
і відповідні їм оригінали  .
.
У випадку, якщо зображення є дрібно-раціональною функцією, тобто:
 ,
,
причому  , а коефіцієнти
, а коефіцієнти  ,
,  - дійсні числа, застосовується формула розкладання Хевісайда:
- дійсні числа, застосовується формула розкладання Хевісайда:
 , (7.17)
, (7.17)
де  - корені рівняння
- корені рівняння 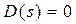 ;
;  - число різних коренів;
- число різних коренів;  - кратність
- кратність  -го кореня.
-го кореня.
Диференціальні рівняння реальних САК мають звичайно прості корені  , і отже для них усі
, і отже для них усі 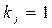 . Тоді вираз (7.17) з урахуванням співвідношення
. Тоді вираз (7.17) з урахуванням співвідношення
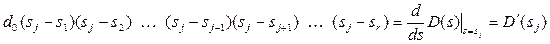
приймає більш простий вигляд
 . (7.18)
. (7.18)
6. Навести криву перехідного процесу.
7. Зробити висновки.
Список літератури
1. Бесекерский В.А. Теория систем автоматического управления / В.А. Бесекерский, Е.П. Попов. М.: “Профессия”, 2004. 747с.
2. Зайцев Г.Ф. Теория автоматического управления и регулирования. 2-е издание перераб. и дополн. Киев: Высшая школа, 1988. 430с.
3. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. М.: Машиностроение, 1973. 606с.
4. Лукас В.А. Теория автоматического управления. М.: Недра, 1990. 416с.
5. Математические основы теории автоматического регулирования / под ред. Б.К. Чемоданова. М.: Высшая школа, 1971. 807с.
6. Мирошник И.В. Теория автоматического управления. Линейные системы. СПб: “Питер”, 2005. 333с.
7. Михайлов В.С. Теория управления. Учебное пособие для ВУЗов. Киев: Высшая школа, 1988. 309с.
8. Пантелеев А.В. Теория управления в примерах и задачах / А.В. Пантелеев, А.С. Бортаковский. М., Высшая школа, 2003. 583с.
9. Попов Е.П. Теория линейных систем автоматического регулирования и управления. М.: Наука, 1989. 496с.
10. Солодовников В.В. Основы теории и элементы систем автоматического регулирования / В.В. Солодовников, В.Н. Плотников, А.В. Яковлев. М.: Машиностроение, 1985. 536с.
11. Теория автоматического управления / под ред. А.В. Нетушила. М.: Высшая школа, 1972. 432с.
12. Теория автоматического управления. Учебное пособие / под ред. А.А. Воронова. Ч.1. М.: Высшая школа, 1987. 367с.
13. Филипс Ч. Системы управления с обратной связью / Ч. Филипс, Р. Харбор. М.: Лаборатория базовых знаний, 2001. 616с.
Зміст
Передмова...……………......…………………………………………......3
1. Основні поняття ТАК...…………..........…………………………......4
2. Математичний опис САК...….……………….……......…………......13
3. Характеристики САК...…………………………………………......26
4. Типові ланки САК і їхні характеристики...........………………......35
5. Стійкість САК.........……………………......……………………......38
6. Якість САК...………………......…………………………………......45
7. Індивідуальне завдання...……………………………………………52
Список літератури...…………………..……………………………......62
Навчальне видання






