Не слишком удачна. Поэтому точечное оценивание обычно служит лишь первым шагом эконометрического моделирования. Следующая действительно важная проблема состоит в том, чтобы определить, насколько «хороши» полученные уравнения регрессии.
Этот вопрос чрезвычайно сложен, и его нельзя рассмотреть сразу, «целиком». Обычно исследование осуществляется в несколько стадий.
Опасаясь неправильной интерпретации, исследователь, прежде всего, составляет общее суждение о полученных результатах, выясняет условия применимости этих результатов.
Затем он прибегает к тем или иным предположениям, которые позволяют построить доверительные интервалы для оцененных параметров (выполнить интервальное оценивание).
3. Наконец, он всеми возможными способами проверяет выполнение предпосылок МНК, чтобы установить степень их реалистичности. Если эти предпосылки оказываются невыполненными, то доверительные интервалы, полученные на предыдущей стадии, не должны приниматься всерьез.
Я стадия – квалифицирование
(с англ. qualify – составить общее суждение о полученных результатах, выяснить условия применимости этих результатов.
На этой стадии, как уже указывалось, решается проблема оценки различных (и очевидных) ограничений, характеризующих либо модель, либо саму выборку, на которых основаны полученные оценки.
Например, агрегированная функция потребления для США (1954 – 1965 г.г.) утверждает, что
С = -3,0 + 0,928 Y + е (в млрд. долл.),
где Y – национальный доход.
Это слишком сильное утверждение. Достаточно допустить, что вследствие какой-либо катастрофы Y круто упадет до 0, то можно ожидать, что С станет отрицательным и достигнет –3,0 млрд. долл?
Дело в том, что при оценивании параметров модели использовались данные, которые ограничивали величину Y: 257 £ Y £ 469 млрд. долл. Поэтому надо быть осторожным при экстраполяции полученных результатов. Кроме того, надо иметь в виду, что на С действуют и другие факторы, а также то, что равновесие между доходами и расходами требует, чтобы
Y = C + I + G – T (а этот факт вообще не был принят во внимание).
2-я стадия – качество аппроксимации (подгонки)
Для выполнения проверки качества подгонки необходимо оценить дисперсию возмущения (s2e). Поскольку e неизмеримая случайная переменная, то ее значение оценивается по остаткам еi, полученным как разность между фактическими и вычисленными по уравнению регрессии:
.
Поэтому естественно предположить (т.к. МНК сводит сумму квадратов остатков к минимуму), что в качестве разумной оценки для s2e можно было бы использовать выборочную дисперсию остатков:
.
Однако можно показать, что математическое ожидание этой оценки (для случая простой регрессии) равно 
. То есть, предложенная оценка 
для s2e является смещенной (заметим, что в случае несмещенности должно быть 
). Чтобы это смещение устранить, надо умножить величину оценк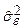и 
на 
. Таким образом, несмещенной оценкой дисперсии возмущения s2e является величина
.
Оценка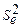 
является также и состоятельной оценкой s2e, так как ее дисперсия стремится к нулю при n ®¥. Число (n – 2), находящееся в знаменателе, называется числом степеней свободы в выборке.
Для многофакторной модели
.
Квадратный корень из дисперсии остатков () называется стандартной ошибкой остатков.
Поскольку 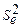вычислена на основе ранее оцененной регрессии Y по Х, то величину 
= 
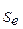называют еще стандартной ошибкой оценки (модели) и обозначают 
.
Оценка дисперсии возмущения (
) служит мерой среднего рассеяния фактических значений (точек) вокруг подобранной линии регрессии; она может дать некоторое представление о возможных достоинствах этой линии регрессии. Эту информацию следует использовать для того, чтобы решить, стоит ли всерьез относиться к подобранной линии регрессии.
