Ранее мы познакомились с простейшими моделями макроэкономических и микроэкономических процессов. При заданных значениях параметров и экзогенных переменных эти модели позволяют предсказывать будущие события. Точность этого предсказания во многом определяется тем, насколько детальна имеющаяся информация.
Одно из основных понятий эконометрии – это ошибка. Определение и сведение ее к минимуму в наших измерениях считается предварительным условием построения модели для предвидения. Причем речь сейчас идет не только и не столько об ошибочных методах измерения, а о правильных, хорошо подобранных методах, но имеющих границы точности, содержащиеся в их природе.
В конечном счете, успех эконометрического исследования зависит от качества оценок, а последние в свою очередь зависят от точности применяемых методов оценивания (т.е. от способов получения оценок).
При любых способах оценивания отдельные выборки содержат обычно неодинаковые наблюдения; в результате этого оценки одного и того же параметра различаются между собой. Но ведь существует только одно истинное значение параметра, и, следовательно, мы не можем рассчитывать на то, что каждая из полученных нами оценок правильна. Вообще мы не можем требовать, чтобы какая-либо из этих оценок в точности совпадала с истинным значением параметра. Но, стремясь к этому, эконометрик старается использовать хорошие методы оценивания. Критерием успеха служат некие свойства, которые гарантируют хорошие средние результаты в тех случаях, когда проводится достаточно большое количество испытаний.
Подойдем к проблеме оценивания параметров как к проблеме выбора. Задача состоит в том, чтобы установить точные правила (способы оценивания), с помощью которых на основе наблюдений, содержащихся в выборке, можно составить представление о неизвестных значениях параметров (математическом ожидании, дисперсии, коэффициентах регрессии и др.). Естественным требованием является сведение к минимуму ошибок при спецификации формы связи между переменными. Но эти ошибки обнаруживаются через отклонения эмпирических данных Yi от значений регрессии 
, т.е. они формируют значения остатков еi, являющихся оценками возмущения e:
. (2.7)
Классический подход к оцениванию параметров линейной регрессионной модели основан на применении метода наименьших квадратов (МНК), который позволяет определить такие оценки, при которых сумма квадратов отклонений фактических значений результативного признака от расчетных (теоретических) минимальна:
.
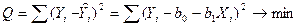Необходимым условием существования минимума функции Q является равенство нулю ее первых частных производных по b0 и b1, и при этом вторые частные производные должны быть положительными.
Найдем первые частные производные и, приравняв их нулю, получим систему уравнений, решение которой и дает искомые значения оценок параметров модели:
, (2.8)
.
Определим вторые частные производные функции Q:
Очевидно, вторые производные положительны.
Поскольку речь идет о функции двух переменных, то для существования минимума функции требуется также выполнение достаточного условия в виде:
.
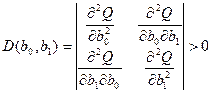Для определения величины D(b0, b1) вычислим недостающие производные:
.
Тогда
если хотя бы одно значение 
Итак, функция Q (b0, b1) достигает минимума, если b 0 и b 1 определяются из условия (2.6). Из системы уравнений (2.8) получаем так называемую систему нормальных уравнений:
,
. (2.9)
Для решения системы нормальных уравнений можно применить правило Крамера, в соответствии с которым величина искомых оценок параметров модели равна:
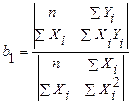, откуда 
(2.10)
Аналогично: 
Можно получить значения b 0 и b 1 несколько иным способом. Разделим первое уравнения системы (2.9) на n:
или 
,
т.е. прямая линия, уравнение которой мы получили, проходит через точку 
. Из этого уравнения имеем:
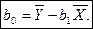(2.11)
Подставив (2.11) в (2.6), получим:
= 
, или 
.
Перейдем к так называемым центрированным переменным, представляющим собой отклонения значений Хi, Yi от средних по выборке. Для этого передвинем начало координат в точку (
), лежащую на прямой регрессии (см. рис.3), и введем следующие обозначения:
, 
и 
.
Тогда в новой системе координат (x, y) постоянная регрессии обратится в 0 (прямая проходит через начало координат), коэффициент b1 не изменится (наклон прямой к оси абсцисс тот же) и уравнение регрессии примет вид (так называемое уравнение в отклонениях):
.
Отклонения фактических значений от расчетных теперь будут равны:
.
Сумма квадратов остатков при этом составит:
.
Y y
Yi yi M (Xi,Yi)
 |
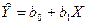
xi x
()
 |
0 Xi X
Рис. 3
Минимизация этой суммы приводит к следующему выражению для определения величины b 1:
, или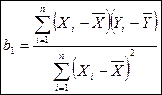 
(2.12)
Используются и другие подходы для определения коэффициентов регрессии. Так, разделив числитель и знаменатель (2.12) на (n- 1), получим в знаменателе дисперсию Х, а в числителе – ковариацию Х и Y:
. (2.13)
Ввиду того, что 
, а 
, то
. (2.14)
Вернемся к примеру о затратах на рекламу и выполним расчет оценок параметров модели с помощью МНК (см. табл. 2).
Таблица 2
| У | Х | УХ | Х2 | У2 |
| Итого: 289 |
Используя данные таблицы 2, рассчитаем оценки параметров модели:
,
.
Подставив эти значения в линейную модель, получим функцию, выражающую зависимость объема продаж от затрат на рекламу:
= -18,02 + 0,345Х.
Это уравнение показывает, что прирост затрат на рекламу в размере 1 грн. обусловливает в среднем увеличение продажи товара фирмы на сумму 0,345 тыс. грн.
Но не следует забывать о том, что этот вывод основан на малом объеме данных. Кроме того, верность интерпретации зависит от верности спецификации модели. Поэтому следует оценить реальность полученных оценок (т.е. определить доверительные интервалы для параметров модели).
