Основная задача математической статистики состоит в установлении распределения реальной случайной величины или ее числовых характеристик по наблюдаемым значениям этой величины, причем используя не всю совокупность возможных значений (генеральную совокупность), а лишь часть ее - выборку. Задача ставится не об отыскании точных значений числовых характеристик, а лишь об их значениях, найденных с той или иной степенью вероятности.
В настоящее время статистические методы широко используются при решении многих технических вопросов. В частности, эти методы используются в строительной механике при исследовании: устойчивости конструкций с учетом возможных отклонений задаваемых условий от реальных; колебаний упругих систем под действием случайных нагрузок; накопления повреждений в результате различных случайных воздействий.
Теоретической основой для разработки методов математической статистики служит теория вероятностей. Возможность применения математического аппарата теории вероятностей для описания реальных процессов окружающего мира обоснована серией специальных законов теории вероятностей – законов больших чисел.
Законы больших чисел.
Оп. 1. Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат может быть предсказан с большой степенью определенности.
Оп. 2. Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Т. 1. (неравенство Чебышева). Для любой случайной величины, имеющей математическое ожидание 
и дисперсию 
, справедливо неравенство:
(1)
Проведем доказательство для НСВ.
Т. 2. (теорема Чебышева). Если дисперсии 
независимых случайных величин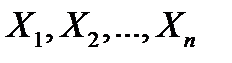 
ограничены одной и той же постоянной 
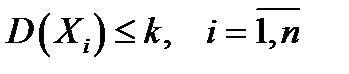, то при неограниченном увеличении числа средняя арифметическая случайных величин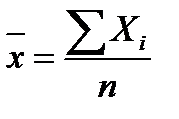 
сходится по вероятности к средней арифметической их математических ожиданий:
(2)
. Рассмотрим неравенство Чебышева для НСВ 
: 
. Если все НСВ 
одинаковые, то 
.
Показано, что при достаточно большом количестве испытаний СВ Х ее среднее значение сколь угодно мало отличается от математического ожидания. Если все измерения значения Х проводятся с одинаковой точностью, характеризуемой дисперсией, то 
. Средний ожидаемый разброс средней независимых измерений в 
раз меньше разброса каждого измерения. Таким образом, увеличивая число измерений, можно как угодно уменьшать влияние случайных погрешностей.
Т. 3. (теорема Бернулли). Относительная частота события в повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью 
при неограниченном увеличении числа сходится по вероятности к вероятности этого события в отдельном испытании: 
.
Пусть 
- ДСВ числа проявлений с. с. в 
испытании. Такие ДСВ могут принимать значения 0 или 1 и распределены по закону Бернулли с параметрами 
. Применим к ДСВ теорему Чебышева: 
Теорема Бернулли объясняет, почему относительная частота, при достаточно большом количестве испытаний, обладает свойством устойчивости и оправдывает данное в теории вероятностей статистическое определение понятия вероятности.
Т. 4. (центральная предельная теорема – ЦПТ). Если 
— независимые случайные величины, у каждой из которых существует математическое ожидание 
и дисперсия 
. Пусть в сумме 
нет слагаемых, влияние которых на разброс значений суммы подавляюще велико по сравнению с остальными. Тогда закон распределения суммы при 
неограниченно приближается к нормальному с математическим ожиданием 
и дисперсией 
.
Замечание. В частности, если все случайные величины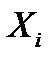 
одинаково распределены, то закон распределения их суммы неограниченно приближается к нормальному закону при 
.
Лекция №2. Выборочный метод.
Генеральная и выборочная совокупность. Выборочный метод. Виды выборок. Дискретные и непрерывные вариационные ряды, их характеристики и графическое изображение.
