Лабораторная работа № 4
Определение коэффициента теплопроводности твердых материалов
методом стационарного теплового режима
Цель работы - ознакомиться с основными методиками и аппаратурным обеспечением экспериментального определения коэффициента теплопроводности горных пород, теплоизоляционных и сыпучих материалов и приобретение навыков работы на электронном измерителе теплопроводности типа ИТП-МГ4 «100».
Теплообмен - самопроизвольный необратимый процесс передачи тепла между телами или частями тела, обусловленный неоднородностью температурного поля. В зависимости от механизма переноса тепла различают три основных вида теплообмена: кондуктивный (теплопроводность), конвективный (конвекция) и лучистый (излучение, радиационный).
Изучая явление теплопроводности, Ж. Фурье (1822 г.) установил, что при установившемся тепловом режиме количество передаваемого тепла Q пропорционально градиенту температуры, времени и площади сечения, перпендикулярного направлению распространения тепла. Математическое выражение для определения величины Q, переданного теплопроводностью, называется основным законом теплопроводности – законом Фурье. В реальных параметрах процесса теплообмена закон Фурье описывается, как
, (1)
Коэффициент λ в уравнении (1) есть физический параметр вещества, который численно оценивает способность вещества проводить тепло при кондуктивном теплообмене и называется коэффициентом теплопроводности (вт/м·К). Значения коэффициента теплопроводности веществ находятся в пределах l» 0,006 ¸ 430 Вт/(м ∙ К). Минимальную теплопроводность из всех веществ имеют газы. Их коэффициент теплопроводности находится в пределах l» 0,006 ¸ 0,2 Вт/(м∙К). Вызвано это слабыми связями между молекулами газов.
В практике теплотехнических расчетов широко пользуются понятием теплового потока QП (Вт). Величину QП можно определить, разделив левые и правые части (1) на время:
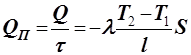; (2)
Таблица 1
Значения коэффициентов теплопроводности газов при Т = 300 К
и абсолютном давлении Р = 101325 Па
| Газ | l∙103, Вт/(м∙К) | Газ | l∙103, Вт/(м∙К) | Газ | l∙103, (Вт/м∙К) |
| N2 | 25,9 | CH4 | 34,3 | C2H6 (этан) | 21,4 |
| O2 | 26,6 | CO2 | 16,6 | H2S | 14,8 |
| CO | 25,2 | SO2 | 9,7 | H2 | |
| C2H4(этилен) | 20,6 | H2O* (пар) | 24,6 | Воздух (сухой) | 18,0 |
* при Т = 373,15 К
Значения коэффициента теплопроводности жидкостей изменяются в пределах l» 0,07 ¸ 1,0 Вт/(м∙К).
Теплопроводность твёрдых тел в подавляющем большинстве случаев обусловлена двумя механизмами: движением электронов проводимости (электронная проводимость) и тепловыми колебаниями атомов их кристаллической решётки (фононная проводимость). Лучшими проводниками теплоты являются металлы, у которых коэффициент теплопроводности l» 8 ¸ 430 Вт/(м ∙ К).
Наиболее теплопроводным металлом является чистое серебро, у него при Т» 300 К l» 430 Вт/(м ∙ К). При этой температуре чистая медь имеет l» 413 Вт/(м ∙ К), чистое золото - l» 400 Вт/(м ∙ К), а чистый алюминий -
l» 237 Вт/(м ∙ К). Коэффициент теплопроводности металлов очень чувствителен к примесям. Например, при появлении в меди даже следов мышьяка (Аs) ее коэффициент теплопроводности снижается с l» 400 Вт/(м ∙ К) до
l» 142 Вт/(м ∙ К).
Таблица 2
Приближённые значения коэффициентов теплопроводности ряда чистых металлов и металлических сплавов при Т = 300 К и абсолютном давлении Р = 101325 Па
| Металл, металлический сплав | l, Вт/(м∙К) | Металл, металлический сплав | l, Вт/(м∙К) |
| Вольфрам | Натрий | ||
| Железо | Никель | ||
| Молибден | Свинец | ||
| Цинк | Титан | ||
| Платина | Кобальт | ||
| Углеродистые стали | 48…59 | Высоколегированные стали | 14…44 |
| Алюминиевые сплавы | 100…160 | Латуни | 100…106 |
| Бронзы | 23…95 | Чугуны | 30…51 |
| Никелевые сплавы | 12…42 | Титановые сплавы | 8…10 |
Минералы и горные породы, как правило, являются плохими проводниками тепла. Они занимают в ряду твёрдых тел сравнительно узкую полосу с малыми значениями теплопроводности - λ» 0,1…7 Вт/(м∙К), так как теплопроводность минералов горных пород в основном имеет фононный характер.
Большой теплопроводностью, λ» 30…200 Вт/(м∙К), обладают лишь некоторые рудные минерал (сфалерит, пирит) и драгоценные камни с практически идеальной кристаллической решёткой (алмаз). Из породообразующих минералов большим значением теплопроводности обладает кварц, λ» 7…12 Вт/(м∙К). Поэтому у плотных малопористых безрудных пород наблюдается повышение λ с увеличением содержания в них кварца.
Таблица 3
Коэффициенты теплопроводности ряда горных пород
при Т = 300 К и абсолютном давлении Р = 101325 Па
| Горные породы | l, Вт/(м∙К) | Горные породы | l, Вт/(м∙К) |
| Граниты | 2,15…5,49 | Глины | 0,83…2,98 |
| Гнейсы | 2,24…2,97 | Песчаники | 1,80…4,80 |
| Габбро | 2,44…3,32 | Сильвиниты | 2,00…6,00 |
| Пироксениты | 2,30…3,60 | Известняки | 1,11…3,00 |
| Кварциты | 1,50…5,34 | Алевролиты | 1,44…1,99 |
| Дуниты | 1,93…2,93 | Угли | 0,14…1,56 |
| Гранодиориты | 1,00…3,17 | Глинистые сланцы | 1,15…2,48 |
| Железистые кварциты | 2,85…4,48 | Аргиллиты | 0,95…2,41 |
| Доломиты | 3,10…4,00 | Гипсы | 0,60…1,20 |
| Базальты | 0,44…3,50 | Каменная соль | 1,70…5,50 |
| Туфы | 1,30…4,00 | Мел | 0,82…2,20 |
Большая сложность процесса передачи тепла в газообразных, жидких и твёрдых веществах не позволила пока разработать теоретических основ для расчётов их λ. Поэтому на сегодняшний день величины λ для всех веществ определяются экспериментально.
Все эти методы могут быть разделены на четыре основные группы:
1) методы стационарного теплового режима;
2) методы регулярного теплового режима;
3) методы квазистационарного теплового режима;
4) методы, основанные на определении параметров нестационарного теплового режима в первой стадии его развития.
1. Все методы, основанные на стационарном тепловом режиме, разделяются на плоские, цилиндрические и сферические в соответствии с формой испытуемого образца. Связь между искомой величиной λ и величинами, получаемыми непосредственными измерениями, в общем виде выражается следующим уравнением:
, (3)
где Q – количество тепла, протекающего от одной изотермической поверхности образца с температурой Т1 к другой с температурой Т2, Дж;
t – время проведения опыта, с; Кф – коэффициент формы слоя исследуемого вещества; λ – коэффициент теплопроводности исследуемого вещества при температуре Т = 0,5(Т1 + Т2), Вт/м∙К.
Все лабораторные установки для определения λ работают на электрической энергии, что позволяет отношение Q / t в (3) определять как произведение силы тока в рабочем нагревателе I на напряжение на его концах U, то есть 
. Соответственно, величины I и U должны измеряться при установившемся тепловом режиме. методы стационарного теплового режима зачастую требует довольно большого времени для эксперимента, иногда не менее 8 часов.
Метод плоского слоя (метод пластины)
Этот метод позволяет определить теплопроводность от строительных плит толщиной d = 50…500 мм до монолитных материалов с d = 1…5 мм в диапазонах λ = от 0,1 до 5 Вт/(м∙К) и температур от –180°С до 1000°С. Ввиду того, что горные породы в основном имеют λ < 5 Вт/(м∙К), метод плоского слоя часто используется для определения их λ.
Образцы твёрдых материалов выполняются либо в виде дисков диаметром D и толщиной d, при этом D > 10d, либо в виде пластин, которые имеют такие же соотношения между продольными размерами пластин и их толщиной.
Метод цилиндрического слоя (метод трубы)
Этот метод из-за сложности изготовления образцов для горных пород не применяется. Он используется только для определения λ теплоизоляционных материалов.
Метод сферического слоя (метод шара)
Данный метод применяется главным образом для определения λ дисперсных твёрдых веществ, к которым относятся и разрыхленные породы (пески, гравий, щебень) при температурах до 1000 К. Наибольшая точность метода достигается при исследовании дисперсных (сыпучих) твёрдых веществ с λ < 0,2 Вт/м∙К.
Рис.1. Принципиальная схема установки для определения коэффициента
теплопроводности методом плоского слоя:
0 – термопара для измерения температуры наружной поверхности боковой изоляции; 1 – термопара в верхнем холодильнике; 2, 3 – термопары в верхней
части нагревателя; 4 – термопара в нижнем холодильнике; 5, 6 – термопары
в нижней части нагревателя; 7 – образцы исследуемого материала; 8 – электрический нагреватель; 9 – холодильники; 10 – тепловая изоляция; 11 – образцовое сопротивление; 12 – делитель напряжения; 13 – автотрансформатор; 14 – автоматический измерительный комплекс; 15 – универсальный цифровой прибор; 16 – переключатель.
К достоинству этого метода относится возможность получения практически идеального одномерного теплового поля без применения специальных устройств, а к недостаткам – сложность монтажа, необходимость строгой центровки шаров исследуемым материалом, трудность равномерного заполнения полости между сферами исследуемым материалом и сложность учёта потерь тепла по электродам нагревателя.
Электронный измеритель теплопроводности ИТП МГ4 «100»
Рис. 2. Общий вид прибора ИТП МГ4 «100»:
1 – стационарная тепловая установка образцов; 2 – измерительная ячейка
для размещения образца; 3 – электронный блок.
Рис.3. Основные конструктивные элементы ИТП МГ4 «100».
Микропроцессорный прибор ИТП МГ4 «100», общий вид которого представлен на рис.2, а основные конструктивные элементы на рис.3, предназначен для оперативного определения величин λ и 
(термическое сопротивление слоя материала 
аналог удельного электрического сопротивления материала и электрического сопротивления проводника 
, δ – толщина слоя материала) твёрдых строительных материалов, в том числе и горных пород, рассмотренным выше методом плоского слоя. Принцип работы прибора основан на автоматическом измерении перепада температур на поверхностях образца, выполненного либо в виде пластины, либо в виде плоского слоя сыпучего материала, при установившемся тепловом режиме.
Прибор позволяет определять теплопроводность и термическое сопротивление материалов при средней температуре образца от +15 до +42,5°С, обеспечивая автоматическое регулирование температур холодильника и нагревателя в процессе испытаний.
Эксперимент проводится в автоматическом режиме, результаты эксперимента выводится на дисплей электронного блока.
