Для вычисления поляризации среды рассмотрим классическую осцилляторную модель атома, предложенную Лоренцем. Поскольку главную роль в оптической активности атома играет электрон, мы для удобства будем говорить именно о движении электрона во внешнем поле. Однако все дальнейшие рассуждения остаются в силе и для иных заряженных частиц, входящих в состав атома. Например, при исследовании дисперсии в области инфракрасных волн необходимо учитывать влияние ионов, способных к колебаниям.
Молекулы или атомы диэлектрика будем рассматривать как системы, в состав которых входят электроны, находящиеся внутри молекул в положении равновесия. Под влиянием внешнего поля это равновесие нарушается: заряды e смещаются на расстояние r (рис.1), образуя при этом дипольный момент 
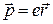. Если в единице объема среды находится N атомов, то возникает дипольный момент
, (8)
имеющий смысл оптической поляризации среды. Поскольку смещение электрона происходит под действием внешнего светового поля, то 
. Для установления явного вида этой зависимости составим и решим уравнение движения электрона во внешнем поле.
В классическом приближении для одномерного движения вдоль оси x уравнение Ньютона имеет вид:
,
где m – масса электрона; в правой части – сумма всех действующих на электрон сил. Сила, удерживающая электрон в положении равновесия, имеет характер упругой силы (квазиупругая сила): 
, где 
- соответствующая константа упругой связи. Силу, вызывающую затухание колебаний, можно считать пропорциональной скорости движения электрона, подобно тому, как в механике сила трения считается пропорциональной скорости движения частицы: 
, где h - коэффициент сопротивления, зависящий от природы среды. Наконец, внешняя сила, вынуждающая электрон совершать колебания,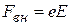 
. Учитывая характер действующих сил, уравнение затухающего вынужденного колебания будет иметь вид:
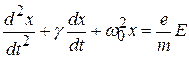. (9)
Здесь 
- параметр, описывающий затухание, 
- квадрат собственной частоты колебаний электрона в атоме.
Поскольку вынуждающая внешняя сила имеет характер волновой функции 
, то и решение уравнения (9) ищем в виде 
. Дифференцируя это выражение и подставляя в (9), находим
,
соответственно
.
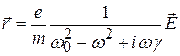Используя это решение, определяем, согласно (7), поляризацию среды:
. (10)
Полученное выражение есть не что иное, как материальное уравнение для света в среде.
Сравнивая (10) и (4), находим формулу для линейной оптической восприимчивости среды в модели Лоренца:
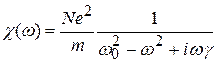(11)
Принимая во внимание (3), можно записать
, (12)
или с учетом (11)
. (13)
Формула (13) дает выражение для комплексной диэлектрической проницаемости в модели Лоренца. По определению для немагнитных сред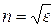 
, значит и показатель преломления 
- комплексная величина. Полученное решение позволяет объяснить целый ряд явлений, связанных с дисперсией и поглощением света.
