Единую модель для всей сложной системы принято называть макромоделью. Обычно такая модель достаточно проста и груба, она годна лишь для приблизительных оценок и самых общих выводов о системе. Попытки уточнить макромодель почти всегда ведут к такому росту ее сложности (размерности), что эффективное рассмотрение модели превышает возможности даже самых современных ЭВМ.
Чтобы выйти из этого положения, надо при моделировании системы вводить декомпозицию и деление на модули, при необходимости строить иерархию моделей, рассматривать потоки информации между отдельными моделями и т. д. Полученная совокупность моделей повторит структуру и иерархию самой системы.
Итак, основной спецификой моделирования сложной системы является учет связей между отдельными моделями (говорят также: согласование моделей). Как же это достигается? В самом общем плане можно указать, что строится схема взаимосвязанных моделей типа графовой структуры, в которой выходы одних моделей (модулей) являются входами других. При этом каждый отдельный модуль представляет собой модель в смысле определений (2.1) или (2.3). Для них фиксируется совокупность требований на входы. Работу с совокупностью моделей можно представить как «прохождение» задачи через эту совокупность, результатом которого является определение выходов сложной системы в целом.
Можно указать на две важные части описанной процедуры:
1) построение или выбор моделей для декомпозированных частей системы;
2) согласование моделей.
Эти части достаточно различны по содержанию. В первой, как известно, ищется формальное, чаще всего математическое описание; во второй организуется совместное использование моделей. Первая требует в основном специальных знаний и навыков формализации; вторая – прежде всего системного подхода. Практическое использование моделей сложных систем чаще всего носит характер имитации. В системе моделей организуется некоторый имитационный процесс, включающий своевременное подключение внешних воздействий и изменение условий протекания процессов, передачу информации от одной модели к другой, команды на начало и окончание работы данной модели и т. д.
Виды моделей.
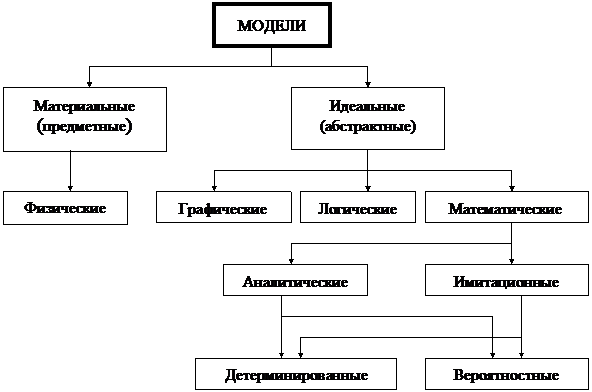 .
.
Математические модели.
Математические модели имеют свою классификацию.
Во-первых, математические модели обычно подразделяются на аналитические и имитационные. В случае аналитических моделей изучаемую систему (объект) и ее свойства удается описать отношениями-функциями в явной или неявной форме (дифференциальными или интегральными уравнениями, операторами) таким образом, что становится возможным непосредственно с помощью соответствующего математического аппарата сделать необходимые выводы о самой системе и ее свойствах (а при синтезе эти свойства в каком-либо смысле оптимизировать). Имитационные модели представляют собой совокупность программ для ЭВМ, с помощью которых воспроизводятся алгоритмы и процедуры, описывающие процесс функционирования исследуемой системы. В этом случае деятельность системы с присущими ей особенностями имитируется на ЭВМ. Многократные машинные эксперименты, результаты которых обрабатываются с помощью методов математической статистики, позволяют изучить и проанализировать свойства данной системы. Имитационные модели обычно используют в тех случаях, когда не удается построить для изучаемой системы достаточно простые и удобные для работы аналитические модели (нередко используется сочетание простых аналитических и более сложных имитационных моделей).
Имитационное моделирование, начиная с 60-х гг., широко применяется в научных исследованиях как в нашей стране, так и за рубежом (в нашей стране такие исследования впервые стали проводить в Вычислительном центре Российской Академии наук). В 1972 г. академиком Н.Н. Моисеевым и его сотрудниками было введено понятие имитационной системы, под которой понимается совокупность системы моделей (основной и вспомогательных), банка данных (общего источника информации) и средств проведения имитационных экспериментов, включающих в свой состав соответствующее математическое обеспечение всего процесса имитационного экспериментирования.
Во-вторых, различают модели детерминированные и стохастические (вероятностные). Первые из них описывают однозначно определенные процессы, течение которых можно полностью предсказать, зная начальные условия и закономерности протекания этих процессов; вторые используют для описания случайных процессов, течение которых описывается законами распределения вероятностей соответствующих случайных величин и однозначно предсказано быть не может.






