Блочные шифры. Сеть Фейcтеля.

Блочный шифр — разновидность симметричного шифра, оперирующего группами бит фиксированной длины — блоками, характерный размер которых меняется в пределах 64 — 256 бит. Если исходный текст (или его остаток) меньше размера блока, перед шифрованием его дополняют. Фактически, блочный шифр представляет собой подстановку на алфавите блоков, которая, как следствие, может быть моно- или полиалфавитной. Блочный шифр является важной компонентой многих криптографических протоколов и широко используется для защиты данных, передаваемых по сети.

В отличие от шифроблокнота, где длина ключа равна длине сообщения, блочный шифр способен зашифровать одним ключом одно или несколько сообщений, суммарной длиной больше, чем длина ключа. Передача малого по сравнению с сообщением ключа по зашифрованному каналу — задача значительно более простая и быстрая, чем передача самого сообщения или ключа такой же длины, что делает возможным его повседневное использование. Однако, при этом шифр перестает быть не взламываемым. От поточных шифров работа блочного отличается обработкой бит группами, а не потоком. Симметричные системы обладают преимуществом над асимметричными в скорости шифрования, что позволяет им оставаться актуальными, несмотря на более слабый механизм передачи ключа (получатель должен знать секретный ключ, который необходимо передать по уже налаженному зашифрованному каналу. В то же время, в асимметричных шифрах открытый ключ, необходимый для шифрования, могут знать все, и нет необходимости в передачи ключа шифрования).

К достоинствам блочных шифров относят сходство процедур шифрования и расшифрования, которые, как правило, отличаются лишь порядком действий. Это упрощает создание устройств шифрования, так как позволяет использовать одни и те же блоки в цепях шифрования и расшифрования. Гибкость блочных шифров позволяет использовать их для построения других криптографических примитивов: генератора псевдослучайной последовательности, поточного шифра, имитовставки и криптографических хэшей.

Сеть Фейстеля — это общий метод преобразования произвольной функции F в перестановку на множестве блоков. Она состоит из циклически повторяющихся ячеек — раундов. Внутри каждого раунда блок открытого текста разделяется на две равные части. Раундовая функция берет одну половину (на рис. правую), преобразует её с использованием ключа Ki и объединяет результат с второй половиной посредством операции исключающее ИЛИ (XOR). Этот ключ задаётся первоначальным ключом K и различен для каждого раунда. Далее половинки меняются местами (иначе будет преобразовываться только одна половина блока) и подаются на следующий раунд. Преобразование сети Фейстеля является обратимой операцией.

Для функции F существуют определенные требования:

· её работа должна приводить к лавинному эффекту

· должна быть нелинейна по отношению к операции XOR

В случае невыполнения первого требования, сеть будет подвержена дифференциальным атакам (похожие сообщения будут иметь похожие шифры). Во втором случае действия шифра линейны и для взлома достаточно решения системы линейных уравнений. Подобная конструкция обладает ощутимым преимуществом: процедуры шифрования/расшифрования совпадают, только производные от первоначального ключи используются в обратном порядке. Это значит, что одни и те же блоки могут использоваться как для шифрования, так и для расшифрования, что, безусловно, упрощает реализацию шифра. Недостаток схемы заключается в том, что в каждом раунде обрабатывается только половина блока, что приводит к необходимости увеличивать число раундов.

Шифр DES.

Основные сведения

Одной из наиболее известных криптографических систем с закрытым ключом является DES – Data Encryption Standard. Эта система первой получила статус государственного стандарта в области шифрования данных. Она разработана специалистами фирмы IBM и вступила в действие в США 1977 году. Алгоритм DES широко использовался при хранении и передаче данных между различными вычислительными системами; в почтовых системах, в электронных системах чертежей и при электронном обмене коммерческой информацией. Стандарт DES реализовывался как программно, так и аппаратно. Предприятиями разных стран был налажен массовый выпуск цифровых устройств, использующих DES для шифрования данных. Все устройства проходили обязательную сертификацию на соответствие стандарту.

Несмотря на то, что уже некоторое время эта система не имеет статуса государственного стандарта, она по-прежнему широко применяется и заслуживает внимания при изучении блочных шифров с закрытым ключом.

Длина ключа в алгоритме DES составляет 56 бит. Именно с этим фактом связана основная полемика относительно способности DES противостоять различным атакам. Как известно, любой блочный шифр с закрытым ключом можно взломать, перебрав все возможные комбинации ключей. При длине ключа 56 бит возможны 2⁵⁶ разных ключей. Если компьютер перебирает за одну секунду 1 000 000 ключей (что примерно равно 2²⁰), то на перебор всех 2⁵⁶ ключей потребуется 2³⁶ секунд или чуть более двух тысяч лет, что, конечно, является неприемлемым для злоумышленников.

Однако возможны более дорогие и быстрые вычислительные системы, чем персональный компьютер. Например, если иметь возможность объединить для проведения параллельных вычислений миллион процессоров, то максимальное время подбора ключа сокращается примерно до 18 часов. Это время не слишком велико, и криптоаналитик, оснащенный подобной дорогой техникой, вполне может выполнить вскрытие данных, зашифрованных ^DESза приемлемое для себя время.

Вместе с этим можно отметить, что систему DES вполне можно использовать в небольших и средних приложениях для шифрования данных, имеющих небольшую ценность. Для шифрования данных государственной важности или имеющих значительную коммерческую стоимость система DES в настоящее время, конечно, не должна использоваться. В 2001 году после специально объявленного конкурса в США был принят новый стандарт на блочный шифр, названный AES (Advanced Encryption Standard), в основу которого был положен шифр Rijndael, разработанный бельгийскими специалистами. Этот шифр рассматривается в конце лекции.

Основные параметры DES: размер блока 64 бита, длина ключа 56 бит, количество раундов – 16. DES является классической сетью Фейштеля с двумя ветвями. Алгоритм преобразует за несколько раундов 64-битный входной блок данных в 64-битный выходной блок. Стандарт DES построен на комбинированном использовании перестановки, замены и гаммирования. Шифруемые данные должны быть представлены в двоичном виде.

Шифрование

Общая структура DES представлена на рис. 4.1. Процесс шифрования каждого 64-битового блока исходных данных можно разделить на три этапа:

1. начальная подготовка блока данных;

2. 16 раундов "основного цикла";

3. конечная обработка блока данных.

На первом этапе выполняется начальная перестановка 64-битного исходного блока текста, во время которой биты определенным образом переупорядочиваются.

На следующем (основном) этапе блок делится на две части (ветви) по 32 бита каждая. Правая ветвь преобразуется с использованием некоторой функции F и соответствующего частичного ключа, получаемого из основного ключа шифрования по специальному алгоритму преобразования ключей. Затем производится обмен данными между левой и правой ветвями блока. Это повторяется в цикле 16 раз.

Наконец, на третьем этапе выполняется перестановка результата, полученного после шестнадцати шагов основного цикла. Эта перестановка обратна начальной перестановке.

 

 

Режимы шифра DES.

DES (англ. d ata e ncryption s tandard) — алгоритм для симметричного шифрования, разработанный фирмой IBM и утверждённый правительством США в 1977 году как официальный стандарт (FIPS 46-3). Размер блока для DES равен 64 бита. В основе алгоритма лежит сеть Фейстеля с 16-ю циклами (раундами) и ключом, имеющим длину 56 бит. Алгоритм использует комбинацию нелинейных (S-блоки) и линейных (перестановки E, IP, IP-1) преобразований. Для DES рекомендовано несколько режимов:

· ECB (англ. e lectronic c ode b ook) — режим "электронной кодовой книги" (простая замена);

· CBC (англ. c ipher b lock c haining) — режим сцепления блоков;

· CFB (англ. c ipher f eed b ack) — режим обратной связи по шифротексту;

· OFB (англ. o utput f eed b ack) — режим обратной связи по выходу.

 

 

Алгоритм Диффи-Хелмана

Алгоритм Диффи-Хеллмана

Основные сведения

Первая публикация данного алгоритма появилась в 70-х годах ХХ века в статье Диффи и Хеллмана, в которой вводились основные понятия криптографии с открытым ключом. Алгоритм Диффи-Хеллмана не применяется для шифрования сообщений или формирования электронной подписи. Его назначение – в распределении ключей. Он позволяет двум или более пользователям обменяться без посредников ключом, который может быть использован затем для симметричного шифрования. Это была первая криптосистема, которая позволяла защищать информацию без использования секретных ключей, передаваемых по защищенным каналам. Схема открытого распределения ключей, предложенная Диффи и Хеллманом, произвела настоящую революцию в мире шифрования, так как снимала основную проблему классической криптографии – проблему распределения ключей.

Алгоритм основан на трудности вычислений дискретных логарифмов. Попробуем разобраться, что это такое. В этом алгоритме, как и во многих других алгоритмах с открытым ключом, вычисления производятся по модулю некоторого большого простого числа Р. Вначале специальным образом подбирается некоторое натуральное число А, меньшее Р. Если мы хотим зашифровать значение X, то вычисляем

Y = A^X mod P.

Причем, имея Х, вычислить Y легко. Обратная задача вычисления X из Y является достаточно сложной. Экспонента X как раз и называется дискретным логарифмом Y. Таким образом, зная о сложности вычисления дискретного логарифма, число Y можно открыто передавать по любому каналу связи, так как при большом модуле P исходное значение Х подобрать будет практически невозможно. На этом математическом факте основан алгоритм Диффи-Хеллмана для формирования ключа.

Формирование общего ключа

Пусть два пользователя, которых условно назовем пользователь 1 и пользователь 2, желают сформировать общий ключ для алгоритма симметричного шифрования. Вначале они должны выбрать большое простое число Р и некоторое специальное число А, 1 < A < P-1, такое, что все числа из интервала [1, 2,..., Р-1] могут быть представлены как различные степени А mod Р. Эти числа должны быть известны всем абонентам системы и могут выбираться открыто. Это будут так называемые общие параметры.

Затем первый пользователь выбирает число Х₁ (X₁<P), которое желательно формировать с помощью датчика случайных чисел. Это будет закрытый ключ первого пользователя, и он должен держаться в секрете. На основе закрытого ключа пользователь 1 вычисляет число

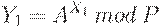
которое он посылает второму абоненту.

Аналогично поступает и второй пользователь, генерируя Х₂ и вычисляя

Это значение пользователь 2 отправляет первому пользователю.

После этого у пользователей должна быть информация, указанная в следующей таблице:

	Общие параметры	Открытый ключ	Закрытый ключ
Пользователь 1	Р, А	Y1	Х1
Пользователь 2	Y2	Х2

Из чисел Y₁ и Y₂, а также своих закрытых ключей каждый из абонентов может сформировать общий секретный ключ Z для сеанса симметричного шифрования. Вот как это должен сделать первый пользователь:

Никто другой кроме пользователя 1 этого сделать не может, так как число Х₁ секретно. Второй пользователь может получить то же самое число Z, используя свой закрытый ключ и открытый ключ своего абонента следующим образом:

Если весь протокол формирования общего секретного ключа выполнен верно, значения Z у одного и второго абонента должны получиться одинаковыми. Причем, что самое важное, противник, не зная секретных чисел Х₁ и Х₂, не сможет вычислить число Z. Не зная Х₁ и Х₂, злоумышленник может попытаться вычислить Z, используя только передаваемые открыто Р, А, Y₁ и Y₂. Безопасность формирования общего ключа в алгоритме Диффи-Хеллмана вытекает из того факта, что, хотя относительно легко вычислить экспоненты по модулю простого числа, очень трудно вычислить дискретные логарифмы. Для больших простых чисел размером сотни и тысячи бит задача считается неразрешимой, так как требует колоссальных затрат вычислительных ресурсов.

Пользователи 1 и 2 могут использовать значение Z в качестве секретного ключа для шифрования и расшифрования данных. Таким же образом любая пара абонентов может вычислить секретный ключ, известный только им.