Это устройство представляет собой опорный элемент (подшипник), внутри которого вращается палец (ось) шарнира. Такая опора не препятствует вращению вокруг оси, но препятствует движению тела в любом направлении в плоскости, перпендикулярной к оси шарнира. Реакция 
такой опоры направлена по нормали к поверхности, на которую опираются катки подвижной опоры. На схемах эту связь изображают так, как показано на рисунке.
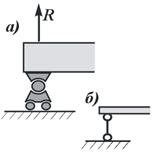
Рисунок. Шарнирно подвижная опора:
а – вид катковой опоры; б – расчетная схема шарнирно-подвижных опор
7. Неподвижная шарнирная опора (рисунок). Реакция R шарнирно-неподвижной опоры расположена в плоскости, перпендикулярной оси возможного вращения, и ее направление определяют две взаимно перпендикулярные составляющие Rx и Ry, соответствующие направлению выбранных осей (рис., а). В строительной механике шарнирно-неподвижную опору изображают в виде двух шарнирных стержней пересекающихся в точке опоры (рис.18, б) или шарнира (рис 18, в). При решении задач будем реакцию 
изображать ее составляющими 
и 
по направлениям осей координат. Если мы, решив задачу, найдем и , то тем самым будет определена и реакция ; по модулю R 
.
Рисунок. Шарнирно-неподвижная
опора:
а – вид шарнирно-неподвижной опоры;
б, в – расчетные схемы шарнирно-неподвижных опор
Способ закрепления, показанный на рисунке, употребляется для того, чтобы в балке не возникало дополнительных напряжений при изменении ее длины от изменения температуры или от изгиба.
8. Стержень. Пусть в какой-нибудь конструкции связью является стержень АВ, закрепленный на концах шарнирами (рисунке). Примем, что весом стержня по сравнению с воспринимаемой им нагрузкой можно пренебречь. Тогда на стержень будут действовать только две силы приложенные в шарнирах А и В. Но если стержень АВ находится в равновесии, то по аксиоме 2 приложенные в точках А и В силы должны быть направлены вдоль одной прямой, т. е. вдоль оси стержня. Следовательно, нагруженный на концах стержень, весом которого по сравнению с этими нагрузками можно пренебречь, работает только на растяжение или на сжатие. Если такой стержень является связью, то реакция 
стержня будет направлена вдоль оси стержня.
9. Неподвижная защемляющая опора или жесткая заделка (рисунке, а). Это соединение исключает возможность каких-либо перемещений абсолютного твердого тела. Балка, изображенная на рисунке а, жестко заделана в стену в точке А. Перемещению ее в вертикальном направлении, препятствует реакция Ry, перемещению в горизонтальном направлении препятствует реакция Rx и повороту вокруг точки А - опорный момент МА. Характерным для данной опоры является наличие опорного момента сил, исключающего вращение тела вокруг любой оси. Схематическое изображение такой опоры в теоретической механике показано на рисунке б. Если под такую балку где-нибудь в точке В подвести еще одну опору, то балка станет статически неопределимой.
С помощью указанных опорных связей сооружения прикрепляются к фундаментам или отдельные элементы соединяются между собой.
Рисунок. Жесткая заделка:
а – вид жесткой заделки; б – расчетная схема жесткой заделки
ОСНОВНЫЕ ПОНЯТИЯ
ВИДЫ СИСТЕМ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО,
И УРАВНЕНИЯ РАВНОВЕСИЯ
Теорема Вариньона — одна из теорем механики, устанавливающая зависимость между моментами сил данной системы и моментом их равнодействующей силы относительно какого-либо центра или оси. Сформулирована для сходящихся сил Пьером Вариньоном в 1687, либо, ещё раньше, Симоном Стевином.
Если система сил, приложенных к абсолютно твердому телу, имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).
Математически выражается равенствами:
или
В ф-ле (1) моменты сил относительно центра О - величины векторные и сумма является геометрической (векторной); в ф-ле (2) моменты сил относительно оси z - величины скалярные и сумма является алгебраической. Моменты относительно центра О могут также рассматриваться как величины алгебраические, когда все силы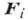 
расположены в одной плоскости и центр О лежит в той же плоскости.
Примерный план (алгоритм) решения задач статики:
1. Назвать (выделить) объект: тело, узел, равновесие которого надо рассмотреть в данной задаче.
2. Указать на рисунке силы, действующие на этот объект:
а) активные силы;
б) назвать каждую связь и пояснить направление реакций связи или их составляющих (мысленно освобождая объект от связи на основании аксиомы освобождения от связей);
3. Назвать вид полученной системы сил, учитывая расположение линий действия сил.
4.Сформулировать условия равновесия полученной системы сил в алгебраической (координатной) форме.
5. Провести на рисунке координатные оси (если заранее не потребовалось это сделать).
6. Составить уравнения равновесия.
7. Решить систему уравнений с пояснением.
8. Сделать проверку.
9. Записать ответ.
