ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
a. Заданную функцию 
на заданном интервале интерполировать заданным полиномами порядка 
. (При расчете сохранять пять знаков после запятой)
b. Рассчитать погрешность интерполирования.
c. Определить значение функции в заданной точке, используя интерполяционные формулы заданных порядков, полученных в п. а и погрешности соотвествующих полиномов по формулам, рассчитанным в п. b.
d. Определить значение функции в заданной точке, используя частный случай интерполяционных формул (по таблице конечных разностей для функций с равноотстоящими точками и полноразмерную (используя все узловые точки) формулу Лагранжа для функций с неравноостоящими точками).
Исходные данные:
| № вар. | 
| Интер-вал | шаг | Интерполяционная формула | 
|
| 
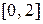
| самост. | Лагранжа | 0.5 |
Решение.
a. Интерполировать таблично заданную функцию полиномами порядка на основе формулы Лагранжа.
Интерполяционная формула Лагранжа:
,
при 
имеем 3 точки
выберем точки
|
| 
|
| 0,50000 | |
| 1,27015 | |
| 1,79193 |
Тогда
При 
имеем 4 точки
выберем точки
|
|
|
| 0,50000 | |
| 0,4 | 0,86053 |
| 1,5 | 1,53537 |
| 1,79193 |
Тогда
При 
имеем 5 точек
|
|
|
| 0,50000 | |
| 0,3 | 0,77767 |
| 0,8 | 1,14835 |
| 1,5 | 1,53537 |
| 1,79193 |
Аналогично находим
B. Рассчитать погрешность интерполирования.
Погрешность интерполяционной формулы Лагранжа
,
.
Найдем производные
C. Определить значение функции в заданной точке, используя интерполяционные формулы заданных порядков, полученных в п. а и погрешности соответствующих полиномов по формулам, рассчитанным в п. b.
,
вычислим погрешность
,
.
аналогично вычисляем
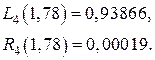
D. Определить значение функции в заданной точке, используя частный случай интерполяционных формул (по таблице конечных разностей для функций с равноотстоящими точками и полноразмерную (используя все узловые точки) формулу Лагранжа для функций с неравноостоящими точками).
По формуле Лагранжа определено значение функции в заданной точке в предыдущем пункте.
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
a. Решить дифференциальное уравнение указанными методами.
b. Определить погрешность численных методов путем двойного пересчета в произвольной точке.
Исходные данные:
| № вар | 
| 
| 
| 
| 
| Метод решения |
| -2 | -1,5 | 0,1 | Формула Эйлера и Метод Рунге-Кутта |
Решение.
A. Решить дифференциальное уравнение указанными методами.
1. Формула Эйлера.
.
Согласно выбранному методу
.
и т.д.
Результаты вычислений сведем в таблицу:
| 
| 
| 
|
| -2,0 | 3,000 | -5,45970 | |
| -1,9 | 2,454 | -5,01633 | |
| -1,8 | 1,952 | -4,60440 | |
| -1,7 | 1,492 | -4,22114 | |
| -1,6 | 1,070 | -3,86292 | |
| -1,5 | 0,684 | -3,52585 |
Таким образом, решение ОДУ имеет вид:
|
|
|
| -2,0 | 3,000 |
| -1,9 | 2,454 |
| -1,8 | 1,952 |
| -1,7 | 1,492 |
| -1,6 | 1,070 |
| -1,5 | 0,684 |
2. Метод Рунге-Кутта.
.
Согласно методу Рунге – Кутта 4-го порядка
,
,
,
,
,
.
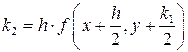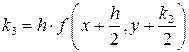Результаты вычислений сведем в таблицу:
|
|
| 
| 
| 
| 
| 
|
|
| -2 | -0,546 | -0,524 | -0,524 | -0,502 | -0,524 | 3,000 | |
| -1,9 | -0,502 | -0,481 | -0,482 | -0,461 | -0,482 | 2,476 | |
| -1,8 | -0,461 | -0,442 | -0,442 | -0,423 | -0,442 | 1,995 | |
| -1,7 | -0,423 | -0,405 | -0,405 | -0,387 | -0,405 | 1,553 | |
| -1,6 | -0,387 | -0,370 | -0,370 | -0,353 | -0,370 | 1,148 | |
| -1,5 | 0,778 |
Таким образом, решение ОДУ имеет вид:
|
|
|
| -2,0 | 3,000 |
| -1,9 | 2,476 |
| -1,8 | 1,995 |
| -1,7 | 1,553 |
| -1,6 | 1,148 |
| -1,5 | 0,778 |
b. Определить погрешность численных методов путем двойного пересчета в произвольной точке.
Вычислим значения 
с шагом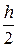 
.
1. Формула Эйлера.
|
| 
| 
|
| -2,0 | 3,000 | 3,000 |
| -1,9 | 2,454 | 2,465 |
| -1,8 | 1,952 | 1,974 |
| -1,7 | 1,492 | 1,523 |
| -1,6 | 1,070 | 1,109 |
| -1,5 | 0,684 | 0,731 |
Погрешность расчета в точке 
.
2. Метод Рунге-Кутта.
|
|
|
|
| -2,0 | 3,000 | 3,000 |
| -1,9 | 2,476 | 2,476 |
| -1,8 | 1,995 | 1,995 |
| -1,7 | 1,553 | 1,553 |
| -1,6 | 1,148 | 1,148 |
| -1,5 | 0,778 | 0,778 |
Погрешность расчета в точке
.
