Если в проводящей среде выделить некоторый объем, по которому протекает постоянный, не изменяющийся во времени ток, то можно сказать, что ток, который войдет в объем, должен равняться току, вышедшему из него, иначе в этом объеме происходило бы накопление зарядов, что не подтверждается опытом. Сумму входящего в объем и выходящего из объема токов записывают так:

Равенство останется справедливым, если обе его части разделить на объем:

Очевидно, что последнее соотношение будет справедливо и в том случае, если объем, находящийся внутри замкнутой поверхности, устремить к нулю:

Таким образом, для постоянного, неизменного во времени поля в проводящей среде
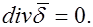
| (42.6) |
Это соотношение называют первым законом Кирхгофа в дифференциальной форме. Оно означает, что в установившемся режиме в любой точке поля нет ни истока, ни стока линий тока проводимости.
Уравнение Лапласа для электрического поля в
Проводящей среде
Напряженность электрического поля в проводящей среде, как и в электростатическом поле,  .
.
В неизменном во времени поле

| (42.7) |
Если среда однородна и изотропна (γ =const), то  можно вынести за знак дивиргенции и, следовательно,
можно вынести за знак дивиргенции и, следовательно,
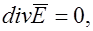
| (42.8) |
или
 . .
| (42.9) |
Таким образом, поле в однородной проводящей среде подчиняется уравнению Лапласа. Поле постоянного тока в проводящей среде является полем потенциальным. В нем, в областях, не занятых источниками, 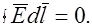
6. Переход тока из среды с проводимостью γ 1 в среду с
проводимостью γ 2. Граничные условия
Выясним, какие граничные условия выполняются при переходе тока из среды с одной проводимостью в среду с другой проводимостью.
 Возьмем на границе раздела сред – линия 00 (рис. 42.2) замкнутый контур 1234. Составим циркуляцию вектора
Возьмем на границе раздела сред – линия 00 (рис. 42.2) замкнутый контур 1234. Составим циркуляцию вектора 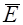 вдоль этого контура. Стороны 12 и 34 его весьма малы по сравнению со сторонами 23 и 41 (длину последних обозначим dl).
вдоль этого контура. Стороны 12 и 34 его весьма малы по сравнению со сторонами 23 и 41 (длину последних обозначим dl).
Так как 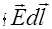 вдоль любого замкнутого контура равен нулю, то он равен нулю и для контура 12341.
вдоль любого замкнутого контура равен нулю, то он равен нулю и для контура 12341.
В силу малости отрезков 12 и 34 пренебрежем составляющими интеграла вдоль этих путей и тогда
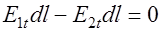 или или 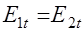 , ,
| (42.10) |
т.е. на границе раздела равны тангенциальные составляющие напряженности поля.
На границе раздела равны нормальные составляющие плотностей токов. Докажем это.
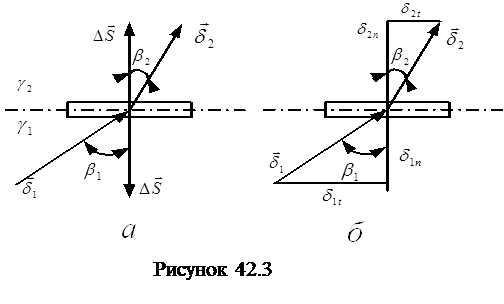 |
На границе раздела выделим сплющенный параллелепипед (рис. 42.3,а). Поток вектора
 , втекающий в объем через нижнюю грань, равен
, втекающий в объем через нижнюю грань, равен  ; поток вектора
; поток вектора  , вытекающий из объема через верхнюю грань
, вытекающий из объема через верхнюю грань  . Так как
. Так как 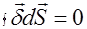 , то
, то
 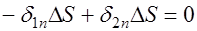 ; ;  . .
| (42.11) |
Следовательно, при переходе тока из среды с одной проводимостью в среду с другой проводимостью непрерывна тангенциальная составляющая вектора 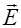 , то есть
, то есть 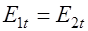 (но
(но  ), и непрерывна нормальная составляющая плотности тока
), и непрерывна нормальная составляющая плотности тока  (но
(но  ).
).
Отсюда следует, что полные значения вектора 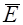 и вектора
и вектора 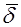 в общем случае меняются скачком на границе раздела.
в общем случае меняются скачком на границе раздела.
Найдем связь между углом падения 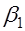 и углом преломления
и углом преломления 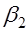 . В соответствии с рис. 42.3,б:
. В соответствии с рис. 42.3,б:
 ; ; 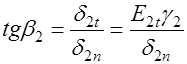 или
или
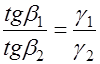 . .
| (42.12) |
Если ток переходит из среды с большой проводимостью (например, из металла) в среду с малой (например, в землю), то тангенс угла преломления 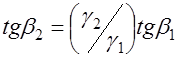 меньше тангенса угла падения и, следовательно, угол
меньше тангенса угла падения и, следовательно, угол 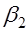 меньше угла
меньше угла 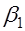 . Если
. Если 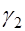 весьма мало, то угол
весьма мало, то угол 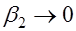 .
.
Вопросы для самоконтроля
1. Какой ток называют током проводимости, а какой – током смещения?
2. Как связаны вектор плотности тока и ток?
3. Проделайте вывод закона Ома в дифференциальной форме.
4. Что понимают под сторонней напряженностью электрического поля?
5. Почему уравнение  называют обобщенным законом Ома, а также вторым законом Кирхгофа?
называют обобщенным законом Ома, а также вторым законом Кирхгофа?
6. Проделайте вывод первого закона Кирхгофа в дифференциальной форме и поясните его физический смысл.
7. Получите выражение для закона Джоуля-Ленца в дифференциальной форме.
8. Докажите, что электрическое поле в проводящей среде подчиняется уравнению Лапласа.
9. Сформулируйте условия на границе раздела двух сред с разной удельной проводимостью.






